NNKJW

XSB

1 Change Of Basis – 基底の変換行列 (change of basis matrix)の概要と計算例

Di: Jacob

As usual, we want to start by . This is an n-by-n matrix where all of the columns are linearly independent, so we know that C is invertible. More generally though, the matrix that we used to transform our basis i, j to Pink’s is called the Change of Basis matrix.Explore math with our beautiful, free online graphing calculator.The change of basis matrix is just a matrix whose columns are these basis vectors, so v1, v2– I shouldn’t put a comma there.本文为《Linear algebra and its applications》的读书笔记目录Change of basisChange of Basis in Rn\mathbb R^nRnChange of basisWhen a basis B\mathcal BB is chosen for an nnn-dimensional vector space VVV , the associated coordinate mapping onto Rn\mathbb R^nRn provides _change of basis

Exploring student ideas on change of basis in quantum mechanics

作成にあたっては「チャート式 . Das hilft uns weiter, da wir so .Find the change of basis matrix P from S to S‘. On the way we’ll see the significance of the matrix of the identity .Microsoft Word – 3-2 Change of basis revised 9-02-19. Step 2: In the numerator, write the logarithm of x with base b.

Solved Consider the following two ordered bases of R3

v = c 1 b 1 + c 2 b 2, and then. Rotations of bases are usually described using rotation matrices, whereas the preferred way to describe rotations of vectors is by using unit quaternions (a. A rotation can be described in two equivalent ways: as a change of basis or as a linear transformation (see dynamical pictures for cool examples from quantum mechanics).If we work with the basis B the transformation takes on a very simple form. It is useful for many types of matrix . Let’s consider two bases B = {v1,v2} B = { v 1, v 2 } and C = {w1,w2} C = { w 1, w 2 } in the two-dimensional real space R2 R 2. The change of basis matrix allows us to write equations where some vectors are expressed in base (left hand side) while others are in base (right hand side). Example – Part 2. In this section we will explain how such a change of basis works. So let’s change the base of log 2., basis) to another, and also how to construct the matrix of a linear transformation with respect to an arbitrary basis.Our calculator simplifies the process of finding transition matrices. spin operator S ˆ .A main theme of linear algebra is to choose the bases that give the best matrix for T.Change of basis is a technique applied to finite-dimensional vector spaces in order to rewrite vectors in terms of a different set of basis elements. Explanation: Let A = (a 1, a 2, . Who are the experts? Experts have been vetted by Chegg as specialists in this subject. Rabiee & Maryam Ramezani 19.Find the change of basis matrix from the basis B to the basis C.

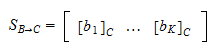
Change of basis | Formula, examples, proofs

However, I cannot wrap my head around what it means that B B (from B =S−1AS B = S − 1 A S) consists of the eigenvalues.

Transformation matrix with respect to a basis

Thales confirmed 2024 annual objectives, refining them as: organic . In other words, you can’t multiply a vector that . Show transcribed image text. Change of Basis.Falls wir noch Zeit haben, erkläre ich dir, warum er Sinn ergibt und wie wir ihn ableiten.06SC Linear Algebra, Fall 2011 View the complete course: https://ocw. x so that it is now in terms of base b, we can apply the following steps: Step 1: Expect a ratio with two logarithmic expressions in terms of base b.Autor: MIT OpenCourseWare

Logarithm change of base rule intro (article)

8k次，点赞4次，收藏6次。 a n) and B = (b 1, ., } are basis of , .

6 Similarity and Change of Basis

b n) bases of V. Then, by the uniqueness of the expansion in a basis, we obtain. That subspace contains w, since w = 3b1 + 2b2.

Change of Basis

77 billion euros, up 26% from prior year, or an increase of 23% on an organic basis. De nition: A matrix B is similar to a matrix A if there is an invertible matrix S such that B = S 1 AS. Der Basiswechselsatz lautet: log_a (b) = (log_x (b)) / (log_x (a)). Therefore those vectors must form some sort of basis.Our research in undergraduate quantum mechanics courses at three institutions explores student thinking about basis, basis expansion coefficients, and change of basis in the context of spin-1⁄2 systems.1 per cent announced in the interim budget. In this paper we investigate the transformations . Matrix representation of linear function CE282: Linear Algebra Hamid R.Der Basiswechsel (Teilgebiet der linearen Algebra) bezeichnet den Übergang zwischen zwei Basen eines endlichdimensionalen Vektorraums über einem Körper K.

Change of basis

Sometimes, it’s useful to remember that matrix multiplication can be expressed as a sum of vectors using linearity. There are 4 steps to solve this one.

Change of Basis

Introduction to Change of Basis - YouTube

Let V be a vector space.On change of basis in quantum mechanics [closed] Homework-like questions and check-my-work questions are considered off-topic here, particularly when asking about specific computations instead of underlying physics concepts. Homework questions can be on-topic when they are useful to a broader audience.The specific way that we translate a vector into a pair of numbers is called a “coordinate system”, and these two special vectors \hat {\imath} ^ and \hat {\jmath} ^ are called the “basis” vectors .Change of Basis. The column of is given by the coefficients of the expansion of in terms of the basis .Wenn dein Ziel ist den Wert des Logarithmus zu finden, ändere die Basis zu 10 oder e , weil dieser Logarithmus auf den meisten Taschenrechner berechnet werden kann.This is 20 basis points lower than 5.Wir können die Basis jedes Logarithmus mittels folgende Regel wechseln: log b. Given a basis A for V, each vector v ∈ V can be uniquely expressed in terms of the base elements vi ∈ A as follows: v = ∑ vi ∈ Arivi.Transformation between arbitrary bases. Using the notation for the coordinates of vector in base : where the sum is taken over a finite number of elements in A. Rabiee & Maryam Ramezani 18.

基底の変換行列 (change of basis matrix)の概要と計算例

Change of basis formula relates coordinates of one and . T ( v) = T ( c 1 b 1 + c 2 b 2) = c 1 b 1 − c 2 b 2. Fiscal deficit is the difference between the expenditure and receipts of the government in a year. Find the change of basis matrix from the basis C to the basis B.Call those vectors of B respectively b1 and b2. It takes a linear transformation, and does a basis change on . matrix , where.The matrix \(P\) is called a \(\textit{change of basis}\) matrix.A change of basis is the transformation of coordinate-based vector and operator representations in a given vector space from one vector basis representation to another.06 Linear Algebra, Spring 2005Instructor: Gilbert StrangView the complete course: http://ocw. We can transform the original data set so that the eigenvectors are the basis vectors amd find the new coordinates of the data points with respect to this new basis; Linear algebra review for change of basis; Graphical illustration of change of basis; Dimension reduction via PCA; Using Singular Value Decomposition (SVD . 当記事では基底の変換行列 (change of basis matrix)の概要と具体例について取り扱いました。 Change of basis Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: September 02, 2019) For spin 1/2 systems, for example, we have the basis { z , z } which are the eigenkets of the.

Logarithmen berechnen: Regel zur Änderung der Basis

These are just the columns– v2 all the way to vn. Any vector v can be written as.edu/18-06S05YouTube Playlist: https://www. The matrix describes a linear map in , which is called the change of basis transformation.

Change of basis in Linear Algebra

Order intake in the first half was 10. Deshalb ändern wir die Basis von log 2. Each representation is characterized by some basis functions.We learned about how vectors can form a basis for a vector space, and we can express any vector within a vector space as a linear combination of the basis ve. One of the basis is related to the other basis through a unitary operator U ˆ , such.

Change of Basis | PDF | Basis (Linear Algebra) | Vector Space

If P P is the matrix which defines the change of the basis (its columns are the coordinates of the new basis vectors in terms of the old basis), then – as you say who know – the formula X = PX′ X = P X ′ (or equivalently X′ = P−1X X ′ = P − 1 X) relates the old ( X X) and new ( X′ X ′) coordinates of a vector. Now, S S consists of the eigenvectors of the matrix.=?−1 ?? Change of basis CE282: Linear Algebra Hamid R. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. You input the initial and final basis, and the calculator provides the transition matrix and a step-by-step breakdown of the calculation. They are independent, and span a subspace W of R4 of dimension 2.In this tutorial, we will desribe the transformation of coordinates of vectors under a change of basis. C is the change of basis matrix, and a is a member of the vector space. Table of contentsMatrix Multiplication and Linear CombinationsDimension TheoremBasisVector SpaceIdentity MatrixHypothesis Testing Expert-verified.Video ansehen50:14MIT 18. We will focus on vectors in R2, although all of this generalizes to Rn. The calculator will find the transition matrix from the first basis to the second basis, with steps shown. This is an n-by-n matrix. Each of these guys are members of Rn and we have n of them. Um dies zu tun, wenden wir die Basiswechselsregel mit b = 2 , a = 50 , und x = 10 an.The Z-score metric constrains the range of values for multiple species over the 20 years of measurements [] and partially addresses the limitations of TPM (thus, RPM \(_{\text {contig}}\)) . ( b) Hinweise: Wenn du diese Eigenschaft verwende, kannst du jede Basis x.We have seen how to convert vectors from one coordinate system (i.Step 1: Find a change of basis matrix from $A$ to the standard basis Step 2: Do the same for $B$ Step 3: Apply the first, then the inverse of the second.When rewriting log a. Since all vectors in R2 R 2 can be represented as linear combinations of v1 v 1 and v2 v . So it’s useful to be able to translate between coordinate systems.Change of basis via PCA.A basis, by definition, must span the entire vector space it’s a basis of. So I followed a guide online which said to express S in terms of S‘: ( 1 −2) =(1 3) a +(3 8) b ( 1 − 2) = ( 1 3) a + ( 3 8) b.Singular Value Decomposition, which is one of the most widely-used techniques in numerical computing, is a basis-change. Or to borrow 3b1b’s verbiage, if Pink gives us a point in their . It allows us to map points on our grid to some other space. Let’s go back to our example. So B is a basis of W.The change of basis formula B = V 1AV suggests the following de nition.We create, for the purposes of deriving an expression for the change of basis, two sets of basis vectors and their corresponding coordinate maps, vectors, and representing matrix. ( 3 −4) =(1 3) c +(3 8) d ( 3 − 4) = ( 1 3) c + ( 3 8) d.Change of basis in polynomial interpolation W.Given two basis matrices basis_old and basis_new in numpy, is there a function somewhere in the library to get the transformation matrix to convert a vector vec in basis_old to its representation in basis_new?.ベクトル空間 V の基底を同じベクトル空間上の基底に写すにあたって用いられる行列を基底の変換行列 (change of basis matrix)といいます。Integration of Radio Frequency Identification (RFID) technology with conductive textiles has greatly expanded the possibilities for creating smart devices that fit perfectly into the concept of . Gander Institute of Computational Science ETH Zurich CH-8092 Zurich Switzerland SUMMARY Several representations for the interpolating polynomial exist: Lagrange, Newton, orthogonal polynomials etc. So I got a = −14, b = 5, c = −36, d = 13 a = − 14, b = 5, c = − 36, d = 13 so would the answer .文章浏览阅读1.Quaternionic change of basis 02 Dec 2016. Our investigation is based on conceptual and computational written questions as well as student reasoning interviews.Example: Evaluating log 2⁡( 50) If your goal is to find the value of a logarithm, change the base to 10 or e since these logarithms can be calculated on most calculators.

3Blue1Brown

matrices

Step 3: In the denominator, find the old base’s logarithm in terms of base b.In this subsection we’re going to work an example of computing matrices of linear maps using the change of basis formula. To do this, we apply the change of base rule with b = 2 , .2 -1 1 1 From here, we were able to plug and chug and come up with [-4 1]T.

1 Change of basis

L(V,W) and Change of Basis CE282: Linear Algebra Hamid R.6 Similarity and Change of Basis We’ve talked in the past about the power of changing coordinate systems.

python

The change of basis is a technique that allows us to express vector coordinates with respect to a new basis that is different from the old basis originally employed to compute coordinates. In particular, we’ve recently noticed that eigenvectors often give us a coordinate system that’s especially well-adapted to working with a given linear transformation. Suppose now that B is another basis for V.

Einführung in die Regel zur Änderung der Basis beim Logarithmus

Change of basis matrix | Alternate coordinate systems (bases) | Linear ...

Rabiee & Maryam Ramezani 20 Important Let T: → be a linear function and u = 1 ⋮ ∈ where ?= 1,.The fact that basis elements change in one way (\(e‘ = e A\)) while coordinates change in the inverse way (\(v‘ = A^{-1} v\)), is why we sometimes call the basis elements covariant and the vector coordinates contravariant, and distinguish them with the position of their indices.change of basis.For the change of basis, S S consisted of the basis vectors of B B and changed them into the basis vectors of E E.Changing the set of basis is referred to as a change of basis. This should serve as a good motivation, but I’ll leave the applications for future posts; in this one, I will . For example, if I have a vector vec = [1,2,3] in the standard basis [1,0,0], [0,1,0], [0,0,1], how to I convert it to another basis, say,edu/18-06SCF11 Instructor: Martina Balagovic A teaching assistant works . By a change of basis from A to B we mean re-expressing v . In this case, we obtain the.

Basiswechsel (Vektorraum)

There are two related concepts in linear algebra that may seem confusing at first glance: change of basis and linear transformation. We may also interchange the role of bases and . Now presumably Y is another basis of W, and I suppose P = MY B =[14 23] means that Y = [y1,y2] with y1 =b1 + 4b2 and y2 = 2b1 + 3b2 (that is, I suppose the columns . There is a quick and dirty trick to obtain it: Look at the formula above relating the new basis vectors \(v’_{1},v’_{2},\ldots v’_{n}\) .