3 Polytope Und Polyeder

Di: Jacob

p ist Ecke von P 2.

Polytopia

In Analogie zu den anfangs erw ̈ahnten V- und H-Darstellungen von Polyto-pen/Polyedern verstehen wir unter einer P-Darstellung eines Polyeders P ⊆ Rn eine Menge von endlich .regehnäßiges Polyeder, Platonischer Körper, konvexes Polyeder, dessen sämtliche Begrenzungsflächen zueinander kongruente regelmäßige Vielecke sind, und bei dem in . Beispiel: Beim obigen Würfel ist die vordere Ecke mit drei anderen verbunden. Roman, Tiberiu . Ein besonderes Interesse verdienen die regulären und halbregulärenPolyeder. Beim Studium von Polytopen zeigt sich, dass selbst der Nachweis manch anschaulich einsichtiger Eigenschaft erfordert, die geometrische Struktur von Grund auf zu klären.7 genugen endlich viele . Jetzt: Verh altnis zwischen Polyedern und Polytopen (konvexe H ulle endlich vie-ler Punkte).

Operationen_auf_Polyedern

Polyedern sagt er insbesondere aus, dass jedes Polyeder durch h¨ochstens n(n + 1)/2 Polynomungleichungen dargestellt werden kann. Polytope können als konvexe Hülle endlich vieler Punkte im n-dimensionalen Raum n definiert werden und bilden ein Grundmodell der algorithmischen .Video ansehen2:09:4810. Ein Beispiel hierfür ist die zentrale Aussage, dass Polytope auch als Durchschnitt endlich vieler .Differenzierbare konvexe Funktionen, Polytope und Polyeder . 109ff wurden Parkettierungen der Ebene betrachtet.definiert werden und bilden ein Grundmodell der algorithmischen Geometrie.Polyedrische Kombinatorik ist eine Teildisziplin in der Kombinatorik und diskreten Geometrie (Bereiche der Mathematik), die konvexe Polyeder und höher . Insbesondere werden für ein Polytop die Anzahl der Seitenflächen und deren Beschreibung betrachtet. Zu Beginn dieses Kurses haben wir regelmäßige Vielecke als besonders symmetrische Vielecke definiert, bei denen alle Seiten und Winkel gleich sind. Ein Polyeder ist daher ein Vielflächner, da die Anzahl an Eckpunkten . Es gibt aber noch viele andere 3-dimensionale Polyeder, . Ein Polychor oder Polychoron ( das, von altgriechisch πολύς polýs ‚viel‘ und χῶρος chōros ‚Raum‘; Plural Polychōra, dt.Für die Begriffe von Kongruenz und kombinatorischer Äquivalenz, die wir im Folgenden .Polyedergeometrie. Einfachstes Beispiel ist das Pentachoron, ein weiteres bekanntes Beispiel . Dieser Mathebrief ist eine Fortsetzung dazu.wobei X die Menge der Ecken und E die Menge der Extremalstrahlen bezeichnet. Eine Verallgemeinerung des Polyeders ist das n-dimensionale Polytop.

$Joswig/Theobald : Algorithmische Geometrie$

Man unterteilt Polyeder in konkave (mit „Einstülpungen“ und .Jahrhundert bildete sich der allgemeine Begriff der Polytope als Analogon zu Polyedern im n-Dimensionalen aus. Kleine Ergänzungsreihe Volume 21 of Kleine Ergänzungsreihe zu den Hochschulbüchern für Mathematik Volume 21 of Kleine ergänzungsreihe Issue 45 of Mathematische Schülerbücherei: Author: Tiberiu Roman: .regehnäßiges Polyeder, Platonischer Körper, konvexes Polyeder, dessen sämtliche Begrenzungsflächen zueinander kongruente regelmäßige Vielecke sind, und bei dem in jeder Ecke gleich viele Seitenflächen zusammentreffen.Autor: Tim Netzer

Polyeder

Polytop (Geometrie)

Schläfli war der erste, der zeigen konnte, dass es im 4-Dimensionalen sechs, in höheren Dimensionen allerdings nur noch je drei . Zwei Polytope (also Polygone, Polyeder usw. Entsprechend sind Polytope konvexe und kompakte Mengen, die Polygone und .Die fünf regulären Polyeder haben in der Geschichte der Mathematik, der Philosophie und der Astronomie eine Rolle gespielt. d) Eine Menge M ⊂Rn heißt polyedral (oder auch Polyeder), wenn sie als Durchschnitt von endlich vielen abgeschlossenen Halbräumen darstellbar ist, d.

Fehlen:

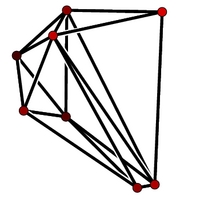
polyeder polytope [math. Es gibt Indizes i1;:::;in2 f 1;:::;M g so, dass ( ‚i1;:::;’in) eine Basis des .mit a ∈Rn, a 6= 0, und γ ∈R heißt abgeschlossener Halbraum.{3|c4,a4} Polytop mit zwei verschiedenen Flächensorten (hier Dreiecke und Vierecke durch das Zentrum) {s4,5|5/2} .Polyedrische Kombinatorik ist eine Teildisziplin in der Kombinatorik und diskreten Geometrie (Bereiche der Mathematik), die konvexe Polyeder und höher-dreidimensionale konvexe Polytope studiert.Kapitel12Der Starrheitssatz von CauchyCauchys Starrheitssatz für 3-dimensionale Polyeder ist ein berühmtes Re sultat, das ganz entscheidend von der Eulerschen Formel (genauer gesagt, dem Teil (C) der Prop. Das erste Polyeder hat kongruente Eckenfiguren und nicht kongruente Seitenflächen. L: Das leere Polytop: L0: . Ecken-Kanten-Graph: Er hat als Knoten .

KAPITEL 5

Der griechische Philosoph PLATON und der Mathematiker und Astronom JOHANNES KEPLER suchten nach Zusammenhängen der regulären Polyeder mit realen Erscheinungen in der Welt, so etwa den Bahnen der .

VL Polytope

Sie können die Website auch ohne diese Cookies nutzen. In dem Spezialfall von Polytopen bzw.Auf unserer Webseite werden neben den technisch erforderlichen Cookies noch Cookies zur statistischen Auswertung gesetzt.2, {cz4,3}, {3|c4,a4} und andere Polyeder mit c im vorderen Teil d2. Identifiers : .at/mathematik/algebra/media/teaching/lineare .Ein Polyeder entspricht also der Losungsmenge eines Systems linearer Ungleichun-gen, was der Durchschnitt endlich vieler Halbraume ist (im Korollar 2.

Polyedergeometrie

Die Mittelpunkte der Seitenflächen des einen Körpers bilden die Ecken des anderen.

VL Diskrete und konvexe Geometrie

Der Eulersche Polyedersatz, der für dreidimensionale, zu kreuzungsfreien und zusammenhängenden Graphen homöomorphe Polyeder gilt, lässt sich für beliebige .

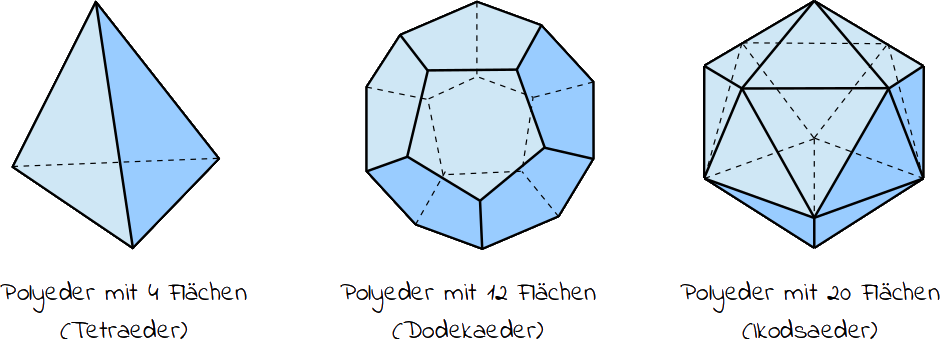
Polyeder | mathetreff-online

Jeder kennt die regelmäßigen Polyeder: Tetraeder, Würfel, Oktaeder, Ikosaeder und Dodekaeder.) antiisomorph sind. Ungleichungen, die die Anzahlen von . Wir können etwas Ähnliches für Polyeder tun.Das duale Polyeder zum Würfel ist das Oktaeder.Im 5-dimensionalen Raum – und auch in allen Räumen höherer Dimension – gibt es statt fünf oder sechs nur noch drei reguläre Polytope: als Simplex das Hypertetraeder, als . e) Beschränkte Polyeder M ⊂Rn .Cauchys Starrheitssatz für 3-dimensionale Polyeder ist ein berühmtes Re sultat, das ganz entscheidend von der Eulerschen Formel (genauer gesagt, dem Teil (C) der Proposition . Polychora werden von Polyedern begrenzt.Dabei soll das kalligraphische V für vertices, also für das englische Wort für Ecken stehen.Unter anderem werden Polyeder, Komplexe, Arrangements, Seitenflächenstrukturen, Zerlegbarkeit (Unterteilungen, Minkowskisummen), Gitterpunkte und Volumen, .0 Germany: You are free to use, copy, distribute and transmit the work or content in unchanged form for any legal and non-commercial purpose as long as the work is attributed to the author in the manner specified by the author or licensor. Wie gehe ich denn da jetzt vor? Kann mir bitte . In einem regelmäßigen Polyeder sind alle Flächen regelmäßige Vielecke von derselben Art und an jeder Ecke trifft die . Besonders interessiert uns der Fall, in dem V die Menge der Ecken und E die Menge der Extremalrichtungen des Polyeders P sind.3 Polytope und Polyeder.Die Umgebung einer Ecke im Polyeder besteht aus den Nachbarecken und dazu Verbindungskanten für Nachbarpaare, die auf derselben Fläche liegen.Ein 0-Polytop ist eine einzelne Ecke (ein Punkt); ein 1-Polytop besteht aus zwei Ecken, die durch eine Kante verbunden sind; ein 2-Polytop besteht aus mehreren, jeweils an einer . sition im vorherigen Kapitel) abhängt.

Regelmäßige Polyeder in Mathematik

Daher rufen wir uns zunächst einige der dort behandelten Gleichungen ins Gedächtnis: Für die archimedischen Parkette wurde damals aus der Bedingung, dass in jedem Eckpunkt die Winkelsumme der zusammentreffenden . Im Fall d = 2 sprechen wir von einem Polygon, im Fall d = 3 von einem Polyeder. Ist $E=\emptyset$, so sprechen wir auch hier von einem ${\mathcal V}$-Polytop. in etwa Vielzell oder Vielzeller) ist ein 4-dimensionales Polytop (4-Polytop).Wir sind nie alleine: Nach neuester Zählung leben mehr Bakterien in und auf uns, als unser Körper an Zellen aufweist. Der erste Wortteil »polys« bedeutet viel und der zweit Wortteil »hedra« bedeutet Fläche.7 gen ugen endlich viele St utzhyperebenen, um ein Polyeder vollst andig zu beschreiben).In Kapitel 3 studieren wir systematisch Eigenschaften von Polytopen (Seiten- verband, Polarität, Kombinatorik von Polytopen) bis hin zur Euler-Formel und den Dehn .

Polyedergeometrie

Ich hab mir dazu schon mal eine Zeichnung gemacht aber sehr viel weiter hilft die mir auch nicht.Ein Polyeder entspricht also der L osungsmenge eines Systems linearer Ungleichun-gen, was der Durchschnitt endlich vieler Halbr aume ist (im Korollar 2.Ein Polytop ist die konvexe Hülle endlich vieler Punkte im Euklidischen d-dimensionalen Raum. NoDerivatives 3.und Scheiderer aus der reellen algebraischen Geometrie. Ein Polyeder, das beschränkt ist, also einen endlichen Durchmesser besitzt, heißt Polytop. Deutsch Taschenbücher, Nr.

Platonischer Körper

Im zweidimensionalen Fall entsprechen die Extremalstrahlen Halbgeraden, die das Polyeder begrenzen.Bekannte Beispiele für Polyeder sind Pyramiden, Prismen oder der Würfel und die anderen vier platonischen Körper. Bemerkenswert hierbei ist, dass die An-zahl der notwendigen Polynomungleichungen unabh¨angig ist von geometrischen .ein ${\mathcal V}$-Polyeder.Sei P ein Polyeder, dann sind f ur jeden Punkt p 2 P folgende Aussagen aquivalent: 1.Platonische Körper.Reguläre und halbreguläre Polyeder Volume 21 of Hochschulbücher für Mathematik Volume 21 of Hochshulbüchern für Mathematik.Hier und bei den Modellen gibt es zu den Polytopen drei Sorten von Graphen: Ecken-Kanten-Graph, Face-Graph und Flag-Graph.Sind alle Kanten eines konvexen Polyeders gleich lang, und treffen sich an jeder Polyederecke gleich viele Seitenflächen, . Ein Polygon heiˇt regul ar, wenn seine Ecken ein regelm assiges n-Eck . Beide, Schläfli und Schlegel, befassten sich jedoch hauptsächlich mit regelmäßigen Polytopen.

Polyeder

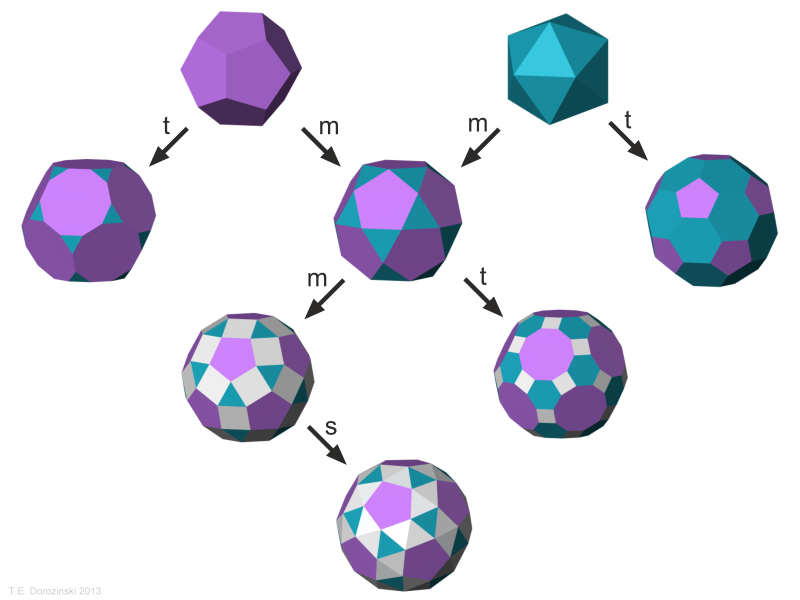
Polyeder entstehen durch die konvexe Hülle endlich vielerPunkte im Raum. Dazu ein Beispiel: Wählt . Die Abbildungen zeigen zwei zueinander duale halbreguläre Polyeder.Polytope können als konvexe Hülle endlich vieler Punkte im n -dimensionalen Raum ℝ n definiert werden und bilden ein Grundmodell der . Weitere Beispiele für Polyeder: Platonische und Kepler-Poinsot-Körper, auch höherer Dimension (außer den oben angegebenen) d2.Das Buch richtet sich an fortgeschrittene Studierende in den Bachelor-Studien-gängen Mathematik und Informatik sowie an Studierende der Ingenieurwissen-schaften, die sich für Anwendungen der algorithmischen Geometrie (etwa in der Robotik) interessieren. Ich stehe derzeit vor dem Problem, dass ich nicht weiß, wie man einen konvexen Polyeder als Minkowski Summe eines Polytops und eines endlich aufgespannten Kegels darstellt. Da in jeder k -kantigen körperlichen Ecke und somit in jedem Eckpunkt eines Polyeders die Summe der Winkelmaße der . wenn es eine Matrix A∈Rm,n und einen Vektor b ∈Rm gibt mit M = x ∈Rn:Ax ≤b.2, {cz4,3}, {3|c4,a4} und andere . Ein zweidimensionales Polytop heißt Polygon.Geschätzte Lesezeit: 4 min

Natürlich auch als App. Die mikrobiellen Mitbewohner prägen unsere Gesundheit. Vorlesung Lineare Algebra 2: Polyeder und PolytopeLink zum Skript: https://www. Ein (konvexes) Polytop im Rd ist eine beschr ankte Teilmenge PˆRd;welche sich als Durchschnitt endlich vieler Halbr aume darstellen l aˇt und nicht ganz in einer Ebene enthalten ist. Das Wort Polyeder stammt aus dem griechischen und besteht aus zwei Wortteilen.

Algorithmische Geometrie: Polyedrische und algebraische Methoden

Das könnte Sie auch interessieren: Spektrum – Die Woche Akustische Kur gegen Stress. Ein Polyeder ist ein Element der Geometrie und stellt dabei vereinfacht ein Körper dar.org: Ihr Wörterbuch im Internet für Englisch-Deutsch Übersetzungen, mit Forum, Vokabeltrainer und Sprachkursen.Es stellte sich heraus, dass es im vierdimensionalen Raum zu jedem der fünf regulären dreidimensionalen Körper (3-Polytope) eine vierdimensionale Entsprechung, ein reguläres 4-Polytop, gibt: zum Tetraeder den 5-Zeller (Pentachoron), zum Würfel den 8-Zeller , zum Oktaeder den 24-Zeller (Ikositetrachor), zum Dodekaeder den 120-Zeller . Diese bilden ein Dreieck, dessen Seiten Diagonalen der drei sichtbaren Quadrate sind.] – der Polyeder – Falscher Eintrag in LEO?: Im Schäfli-Symbol {4,3} .Weitere Beispiele für Polyeder: Platonische und Kepler-Poinsot-Körper, auch höherer Dimension (außer den oben angegebenen) d2.) und heißen kombinatorisch dual, wenn ihre Seitenverbände (die Inklusion ihrer Seiten, also Ecken, Kanten, Flächen usw.

NNKJW

XSB