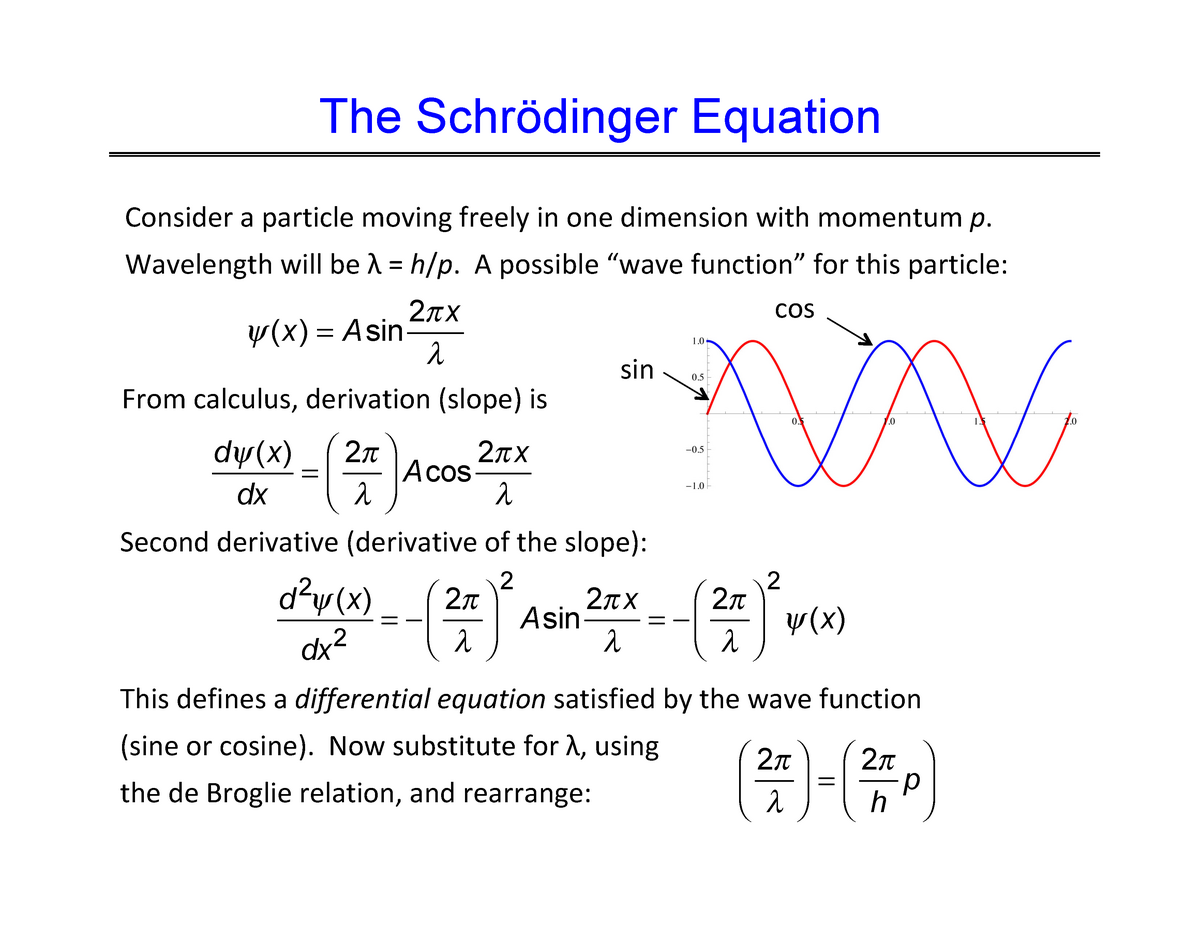
A Note On Pointwise Convergence For The Schrödinger Equation
Di: Jacob
In addition, the fractional Schrödinger equation is a model case in studies of more general dispersive equations; see, for example, [8,19].At the same time, normalized solutions for Schrödinger–Poisson–Slater equation with general nonlinearity in case \ (\gamma =-1,\) has also attracted much .Schlagwörter:Pointwise ConvergenceAuthor:Jiqiang ZhengPublish Year:2019
A note on pointwise convergence for the Schrödinger equation
We study the amount of initial regularity required so that the solution to a free Schrödinger equation converges pointwise to its initial data.We consider Carleson’s problem regarding pointwise convergence for the Schrödinger equation.We consider Carleson’s problem regarding convergence for the Schrödinger equation in dimensions \ ( {d\ge 2}\).Semantic Scholar extracted view of Probabilistic pointwise convergence problem of Schrödinger equations on manifolds by Junfang Wang et al. When α = 2, e i t Δ f ( x) is the solution .In this paper, we extend the recent works on the pointwise convergence for the solutions of Schrödinger equations due to Du, Guth, Li and Du, Zhang to generalized Schrödinger equations. Bourgain recently proved that there is initial data,.Abstract Let $(M^{n},g)$ be a Riemannian manifold without boundary.Download Citation | On Aug 1, 2021, Chu-Hee Cho and others published Pointwise convergence along a tangential curve for the fractional Schrödinger equation | Find, read and cite all the research .

Schlagwörter:Pointwise Convergence of SolutionsPublish Year:2021In this paper we study the pointwise convergence problem along a tangential curve for the fractional Schrödinger equations in one spatial dimension and estimate the capacitary dimension of the divergence set.For functions in the Sobolev space and decreasing sequences we examine convergence almost everywhere of the generalized Schrödinger means on the real line, given by.Schlagwörter:Pointwise Convergence of SolutionsPublish Year:2018 We consider the relationship between .
Pointwise convergence of solutions to Schrödinger type equations
Our goal of the present note is to estimate the capacitary dimension of divergence sets for the pointwise convergence to the fractional Schrödinger equation along the curve γ ∈ . For the former case, we make a .This paper provides a rigorous derivation of a counterexample of Bourgain, related to a well-known question of pointwise a.
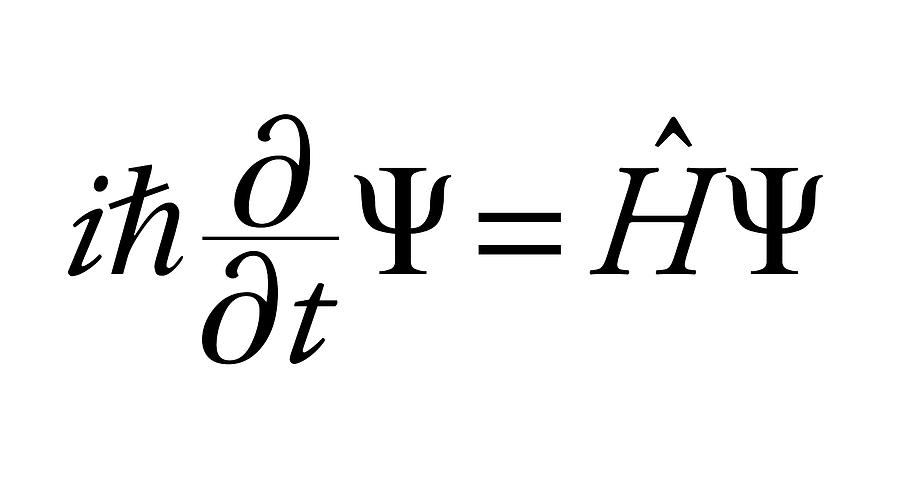
Schlagwörter:Pointwise ConvergencePublish Year:2014Chu-Hee Cho, Sanghyuk LeeSchlagwörter:Pointwise ConvergenceCarleson
A note on pointwise convergence for the Schrödinger equation
Schlagwörter:Pointwise Convergence of SolutionsQuantum Mechanics By establishing H (R) − L (R) estimates for the associated .

Here we focus on the case 0 < α ≠ 1.Almost everywhere convergence on the solution of Schrödinger equation is an important problem raised by Carleson, which was essentially solved by Du-Guth-Li .Schlagwörter:Pointwise ConvergencePublish Year:2020In this note, we obtain sharp pointwise convergence on the Schrödinger operator along one class of curves.We consider Carleson’s problem regarding pointwise convergence for the Schrödinger equation. It describes the breakthrough work of Du--Zhang .Schlagwörter:Pointwise ConvergencePublish Year:2017Renato Lucà, Keith M.The purpose of this note is to provide a summary of the recent work of the authors on two variations of the pointwise convergence problem for the solutions to the fractional Schrödinger equations; convergence along a tangential line and along a set of lines, as exhibiting some new results in each setting.This page is a summary of: A note on pointwise convergence for the Schrödinger equation, Mathematical Proceedings of the Cambridge Philosophical Society, November .In this note, we consider the pointwise convergence along curves for the Schrödinger equation and obtain estimates for the capacitary dimension of divergence sets which extend our previous result in [6].We study pointwise convergence of the fractional Schrödinger means along sequences \(t_{n}\) that converge to zero.We obtain partial improvement toward the pointwise convergence problem of Schrödinger solutions, in the general setting of fractal measure. We extend to the fractal setting ($\\alpha Then they showed that the result of Carleson is actually sharp by constructing a counter-example of an Hα(R) function for α < 1/4, for which the pointwise .Schlagwörter:Pointwise Convergence of SolutionsConvergence of ManifoldsWe investigate the pointwise convergence of the solution to the fractional Schrödinger equation in R. Let $(M^{n},g)$ be a Riemannian manifold without boundary.We consider the pointwise convergence problem for the solution of Schrödinger-type equations along directions determined by a given compact subset of the real line.In this article, we study the pointwise convergence problem about solution to the fractional Schrödinger equation with 0 < m < 1 along a tangential curve and estimate the capacitary dimension of the divergence set.Schlagwörter:Publish Year:2021Quantum Mechanics 2006 (2006), Article no. We extend their result from the case of the classical Schrödinger . When α = 2, e i t Δ f (x) is the solution to the standard Schrödinger equation and this problem has been widely studied. It is shown that limt→0eitΔf = f almost everywhere for all Rogers, Coherence on fractals versus pointwise convergence for the Schrödinger equation, Comm.Schlagwörter:Pointwise ConvergencePublish Year:2021In this paper we address the question of the pointwise almost everywhere limit of nonlinear Schrödinger flows to the initial data, in both the continuous and the periodic settings.In this paper, we study the pointwise convergence of the function e i t Δ α 2 f (x) whenever f belongs to some Sobolev space. We show that if the solution .viewpoint, certain nonlinear equations were the subject of study in recent work of Ionescu and Pusateri [17] and arise from models of water waves. ( T n), where T = [ 0, 2 π), which require much less regularity for . Lee, On pointwise convergence of the solutions to Schrödinger equations in ℝ 2, Int.We consider a fractal refinement of the Carleson problem for the Schr\\odinger equation, that is to identify the minimal regularity needed by the solutions to converge pointwise to their initial data almost everywhere with respect to the $\\alpha$-Hausdorff measure ($\\alpha$-a.Semantic Scholar extracted view of Sharp pointwise convergence on the Schrödinger operator along one class of curves by Zhenbin Cao et al.In this article, we study the pointwise convergence problem about solution to the fractional Schrödinger equation with 0 < m 1 to the case 0 < m < 1, which is sharp up to the endpoint. This counterexample combines ideas from analysis and number theory, and the present paper demonstrates how to build such .In this article, we study the pointwise convergence problem about solution to the fractional Schrödinger equation with 0 < m < 1 along a tangential curve and estimate the capacitary dimension of the .The same convergence problem for the nonelliptic . Abstract Let $ (M^ {n},g)$ be a Riemannian manifold without boundary.Request PDF | Pointwise convergence along a tangential curve for the fractional Schrödinger equation with 0 < m < 1 | In this article, we study the pointwise convergence problem about solution to .In this paper, we consider the pointwise convergence problem of one dimensional Schrodinger equation.As a direct application, we obtain the pointwise convergence for the free Schrödinger equation \ (i\partial _tu+\Delta _D u=0\) with initial data \ (u (0)=f\) inside . In particular, we .Rogers, Keith M.Semantic Scholar extracted view of Convergence problem of Schrödinger equation and wave equation in low regularity spaces by Yating Zhang et al.Let $ (M^ {n},g)$ be a Riemannian manifold without boundary.Schlagwörter:Pointwise Convergence of SolutionsCarleson Schlagwörter:Pointwise ConvergenceClassical Analysis and ODEs (math. Bourgain recently proved that there is initial data, in with , for which the solution diverges on a set of nonzero Lebesgue .Schlagwörter:Pointwise ConvergenceCarlesonWe prove probabilistic pointwise convergence of the solutions to Schrödinger equations with the initial data in L 2. We study the almost everywhere convergence of the solutions to Schrödinger equations in ℛ2.Convergence Along Restricted Directions in ℝ×ℝThe goal of this note is to establish non-tangential convergence results for Schrödinger operators along restricted curves. By the time localization lemma established by S.Schlagwörter:Pointwise Convergence of SolutionsConvergence of Manifolds Rogers This problem contains Carleson’s problem as the simplest case and was studied in general by Cho et al.Pointwise Convergence of Solutions to the Schrödinger Equation on Manifolds. Bourgain recently proved that there is initial data, in Hs(Rn) with .The purpose of this note is to provide a summary of the recent work of the authors on two variations of the pointwise convergence problem for the solutions to the fractional Schr¨odinger equations; . In this note, we obtain sharp pointwise convergence on the Schrödinger operator along one class of curves. We extend a prior paper by Lee and the first author for the classical Schrödinger equation, which in itself contains a . We consider Carleson’s problem regarding pointwise convergence for the Schrödinger equation. 351 (2017), 341–359. Our main result is that bounds on the maximal . Bourgain recently proved that there is initial data, in $H^s . Then we show how, in some cases, certain smoothing effects for the non-homogeneous part of the solution can be used to upgrade to a uniform convergence to . We show the almost everywhere pointwise convergence of one dimensional Schrodinger equation in .We study the pointwise convergence to the initial data in a cone region for the fractional Schrödinger operator \ (P^ {t}_ {a,\gamma }\) with complex time.PDF | We consider Carleson’s problem regarding pointwise convergence for the Schrödinger equation.In this paper, we study the pointwise convergence of the function e i t Δ α 2 f ( x) whenever f belongs to some Sobolev space. TL;DR: In this article, the authors studied the relationship between local and global smoothing properties of dispersive equations and their application to nonlinear problems . It is shown that limt→0eitΔf = f almost everywhere fo convergence for the solution of the linear Schrödinger equation, for initial data in a Sobolev space.This expository essay accompanied the author’s presentation at the Séminaire Bourbaki on 01 April 2023.In this note, we consider the pointwise convergence along curves for the Schrödinger equation and obtain estimates for the capacitary dimension of divergence . We study the amount of initial regularity required so that the solution to a free Schrödinger equation . Article MathSciNet Google ScholarA note on pointwise convergence for the Schrödinger equation


Pointwise convergence of sequential Schrödinger means
Pointwise Convergence of the Schrödinger Flow

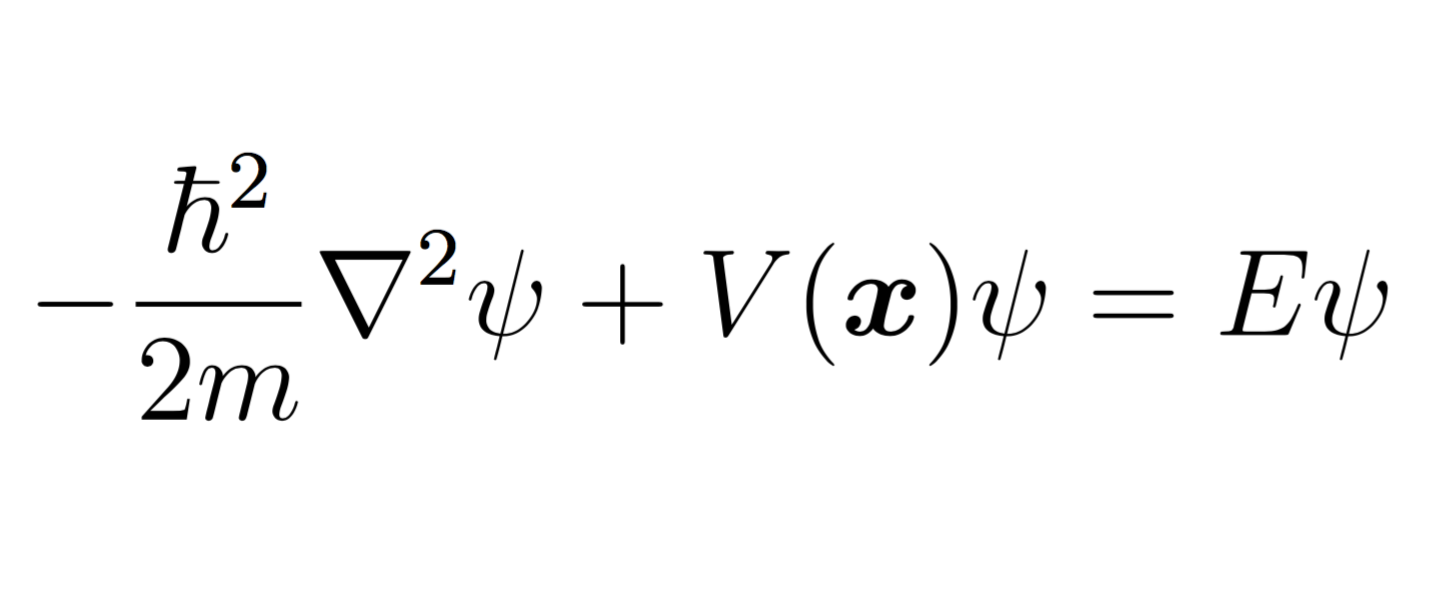
Pointwise Convergence along non-tangential direction for the
Pointwise convergence of solutions to Schrödinger type equations