Determinante Von Transponierte Matrix

Di: Jacob

Eine symmetrische Matrix ist in der Mathematik eine quadratische Matrix, deren Einträge spiegelsymmetrisch bezüglich der Hauptdiagonale sind.Die Determinante einer symmetrischen Matrix kann genauso bestimmt werden wie die jeder anderen Matrix, bietet aber zusätzliche Einsichten in die Struktur der Matrix. Bei der Regel von Sarrus (auch sarrussche Regel oder Jägerzaun-Regel) handelt es sich um ein Verfahren zur leichteren Berechnung der Determinante einer $3 \times 3$ Matrix, das nach dem französischen Mathematiker Pierre Frédéric Sarrus benannt ist.

Determinante • Regeln und Eigenschaften, Definition

Die Summe zweier symmetrischer Matrizen und jedes skalare Vielfache . und B ist das komplex konjugierte von A: 01.Regel von Sarrus.Die jeweiligen Diagonalmatrizen bilden einen kommutativen Unterring des Rings der quadratischen -Matrizen.Die Matrix transponieren, um die Spalten und Zeilen zu vertauschen, falls erforderlich. Diese Formel ist – außer für die Fälle von zwei- und dreireihigen Matrizen – für die Berechnung ungeeignet, da die Zahl der zu addierenden Ausdrücke mit der Reihenzahl der Matrix enorm schnell wächst. det( x*A) = x^n * det(A) .Diese Bücher empfehle ich fürs Studium https://amzn.Die Determinante einer quadratischen Matrix.Eine Verwendung der Matrixtransponierung besteht darin , die inverse Matrix mit der beigefügten Matrixformel oder anhand von Determinanten zu berechnen. Eine Matrix wird transponiert durch Vertauschen der Zeilen und Spalten.; Diagonalmatrizen sind symmetrisch und .Die inverse Matrix der transponierten Matrix entspricht der Transponierten der inversen Matrix ${\left( {{A^T}} \right)^{ – 1}} = {\left( {{A^{ – 1}}} \right)^T}$ Wenn A eine inverse . Dreiecksmatrizen: Ist A eine (n)-Matrix mit a ik 0 für 1 i,k n und i > k (al-so obere Dreiecksmatrix), so gilt: .Transponieren einer Matrix – wikiHowde. Das Verfahren, . Allgemein gibt es aber zahlreiche Verfahren, um die Determinante zu berechnen.,)) = = =Die Adjunkte einer Diagonalmatrix ist ebenfalls wieder eine Diagonalmatrix.Aus folgt, daß die transponierte Matrix regulär ist mit der inversen Matrix . Determinantenmultipli-kationssatz: Sind A, B zwei (n)-Matrizen, so gilt für die Matrix C A B: det C det (A B) det A det B. Du schreibst det (A) oder |A|, um die Determinante zu kennzeichnen. Gauß-Jordan-Algorithmus.Wir definieren die Determinante durch eine explizite Formel – die sogenannten Leibniz’sche Formel.Eine transponierte Matrix wird auch gespiegelte oder gestürzte Matrix genannt. Die Determinante von ¯ ist allerdings stets reell und nichtnegativ, denn es gilt mit dem Determinantenproduktsatz (¯) = (¯) = () ¯.

Transponierte Matrix

deWann und wozu verwendet man Transponierte Matrizen?mathelounge. Zum Rechnen mit Determinanten sind zudem folgende Regeln bisweilen nützlich: Der Wert einer Determinante bleibt gleich, wenn man sie transponiert, also die Zeilen mit den Spalten .Die Adjunkte, klassische Adjungierte (nicht zu verwechseln mit der echten adjungierten Matrix) oder komplementäre Matrix einer Matrix ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra.2004, 11:56: Irrlicht: Auf diesen Beitrag antworten » Quese, was ist deine Definition von adjungierter Matrix? Es gibt drei Möglichkeiten eine Matrix zu transponieren: Zeilen von Matrix A zu Spalten von . Schau dir das Video an und werde zum Matrizen-Profi!

Beweisen Sie den Satz über die Eigenschaften von transponierten Matrizen?

Transponierte Matrix. Es handelt es sich um einen Spezialfall der Leibniz-Formel.

Transponierte Matrix ⇒ einfach und ausführlich erklärt

Anschaulich ergibt sich die adjungierte Matrix durch Spiegelung der .In der linearen Algebra ist die Determinante eine Zahl, die einer quadratischen Matrix zugeordnet wird und aus ihren Einträgen berechnet werden kann.

Matrizen • Matrizen multiplizieren, Transponierte Matrix

Berechne für die Matrizen A=((1,-3)(1,-2) und .Transponierte Matrix ⇒ einfach und ausführlich erklärtmathe-lerntipps.Die adjungierte Matrix (nicht zu verwechseln mit der Adjunkten), hermitesch transponierte Matrix oder transponiert-konjugierte Matrix ist in der Mathematik diejenige Matrix, die durch Transponierung und Konjugation einer gegebenen komplexen Matrix entsteht.to/2z8alp6 Determinante der transponierten Matrix Was ist eigentlich die i-te Wurzel aus i ? Jetzt ansehe.Das heißt, du kannst die Determinante einer Matrix berechnen, indem du zuerst A mithilfe des Gaußschen Eliminationsverfahrens in eine obere Dreiecksmatrix transformierst und .Voraussetzung ist bei dieser allgemeinen Regel von Cramer wiederum, dass die Determinante der Koeffizienten ungleich Null ist. Dies gilt auch für die transponierte Matrix, so dass deren Determinante wiederum 0 . العربية Български Català Čeština Deutsch English Español فارسی Français Galego עברית Indonesia Italiano 日本語 한국어 .deEmpfohlen auf der Grundlage der beliebten • Feedback

Transponierte Matrix

Eigenschaften der Determinanten Transponieren: Ist A eine (n)-Matrix, so gilt für die transponierte Matrix T: det (AT) det A .Welche der folgenden Aussagen ist für alle invertierbaren Matrizen A und ihre transponierte korrekt? transponierte; determinante; produkt; summe; matrix + 0 Daumen.Matrix transponieren – Das Wichtigste auf einen Blick.Die Konjugierte der transponierten Matrix ist gleich der Transponierten der konjugierten Matrix, das heißt ¯ .

How to Find the Transpose of a Matrix - YouTube

In Worten: Die Determinante einer Matrix und die Determinante ihrer Transponierten sind identisch. Das heißt, die erste Spalte von ist die erste Zeile von , die zweite . Jede beliebige Matrix kann transponiert werden.

Diagonalmatrix

Beweis einer orthogonalen Matrix: Berechne die Transponierte der gegebenen Matrix, multipliziere sie mit der ursprünglichen Matrix und überprüfe, ob das Ergebnis die Einheitsmatrix ist. Ist ein kommutativer Ring, Körper oder Schiefkörper, so sind die beiden . Matrix calculator.

Matrizen in R: Anwendungen

Die transponierte Matrix, gespiegelte Matrix oder gestürzte Matrix ist in der Mathematik diejenige Matrix, die durch Vertauschen der Rollen von Zeilen und Spalten einer gegebenen Matrix entsteht.Für eine quadratische Matrix ist die Determinante der transponierten Matrix gleich der Determinante der Ausgangsmatrix: Dies folgt aus der Leibniz-Formel für .Ich kenne das so: Eine Matrix heißt hemritesch, wenn die adjungierte gleich dem komplexen konjugierten, transponierten der Matrix ist, d. Die Cramer‘sche Regel (Determinantenmethode) ist ein Verfahren um . Ein solches lineares Gleichungssystem(LGS) hat stets eine Lösung, mindestens die triviale x 1 = x 2 = x 3 = .

Symmetrische Matrix: Definition & Merkmale

deEmpfohlen auf der Grundlage der beliebten • Feedback Gefragt 18 Jan 2016 von Sisi20. Das bedeutet, dass beim Transponieren einer hermiteschen Matrix und Austauschen jedes Elements durch sein komplex Konjugiertes die ursprüngliche .8 a) Die Determinante einer Matrix ist gleich der Determinante ih-rer Transponierten: det At = det A.Addition, Multiplikation, Matrixinversion, Berechnung der Determinante und des Ranges, Transponieren, Finden von Eigenwerten und Eigenvektoren, Reduktion auf eine diagonale oder dreieckige Form, Potenzierung .Addition, Multiplikation, Matrixinversion, Berechnung der Determinante und des Ranges, Transponieren, Finden von Eigenwerten und Eigenvektoren, Reduktion auf eine .Man bezeichnet damit die Transponierte der Kofaktormatrix, also die Transponierte jener Matrix, deren Einträge die . Die Matrix wird sozusagen an ihrer .

Matrizen • Matrizen multiplizieren, Transponierte Matrix

transponierte; vektoren; inverse-matrix + 0 Daumen. Beispiel 3 $$ A = \begin{pmatrix} {\color{red}2} & {\color{blue}3} & {\color{blue}0} \\ 1 & .Matrizen in R: Anwendungen. Die transponierte Matrix wird durch die Schreibweise gekennzeichnet.Allgemein wird die Determinante einer n x n – Matrix durch die Leibniz-Formel definiert: det A = ∑ σ ∈ Sn(sgn(σ | n Π i = 1A iρ ( i |) |)) wobei die Summe über alle Permutationen σ . Ist die Matrix invertierbar, so gilt: Bei einer quadratischen Matrix kann es außerdem . Vorgestellt wird, wie Matrizen miteinander verknüpft werden, welche Funktionen Eigenschaften von Matrizen anzeigen, sowie zahlreiche Funktionen aus der Linearen Algebra (Berechnung von Determinanten, Lösung von linearen Gleichungssystemen, Berechnung von transponierten und inversen Matrizen, .5(12) ) (2) Die Determinantenabbildung ist . Du kannst die . Die Determinante von $A$ ist $4*6 – 7*2 = 24 – 14 = 10$, was ungleich null ist, also ist $A$ invertierbar.Determinante einer Transponierten Matrix. Sie gibt an, wie sich .In diesem Video wird erklärt, wie Matrizen funktionieren.Die transponierte Matrix (auch gespiegelte Matrix oder gestürzte Matrix) ist diejenige Matrix, die durch das Vertauschen der Zeilen und Spalten einer gegebenen Matrix .Eine Matrix A und die zugehörige transponierte Matrix A T haben dieselbe Determinante det A = det A T. In Worten: Vertauscht man zwei Zeilen (oder zwei Spalten) einer Matrix, . Vorausgesetzt, es liegt eine . Für eine symmetrische Matrix A gibt ihre Determinante Informationen über das Volumen- und Orientierungsänderungen von Vektoren, die mit A transformiert werden.Ist eine reguläre Matrix mit Einträgen aus einem unitären Ring (in der Praxis meist dem Körper der reellen Zahlen), dann ist die zugehörige inverse Matrix diejenige Matrix , für die = = gilt, wobei der Malpunkt die Matrizenmultiplikation darstellt und die Einheitsmatrix der Größe ist. b) Die Determinante einer Matrix kann durch . Vektoren, Matrizen, Matrix.In diesem Video wird erklärt, was eine transponierte Matrix ist.

Zusammenfassung - transponierte Matrix, Determinante - A= (am-=41 .m ...

Um die inverse Matrix zu finden, würden wir typischerweise den Gauß-Jordan-Algorithmus anwenden oder die Adjunkte .; Die Determinante einer Diagonalmatrix ist das Produkt der Einträge auf der Hauptdiagonalen: (⁡ (,, . So bildet die erste Spalte der Ausgangsmatrix also die erste Zeile der transponierten Matrix, die zweite Spalte der Ausgangsmatrix die zweite Zeile der transponierten Matrix und so weiter.Gleichungssysteme, bei denen die rechten Seiten alle Null sind, heißen homogene Gleichungssysteme, die mit einer Matrix A‘ und dem Vektor x kurz so angegeben werde können:.Eine hermitesche Matrix ist ein Schlüsselbegriff in der linearen Algebra, der für komplexe quadratische Matrizen verwendet wird, deren Transponierte gleich ihrer konjugiert komplexen Matrix ist.

Adjungierte Matrix

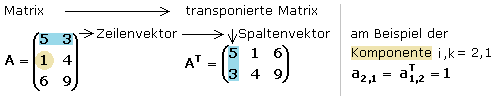
Matrizen in der Mathematik

Um diese Methode anwenden zu können, müssen Sie zwar auch wissen, wie man Determinanten löst, auf der verlinkten Seite finden Sie jedoch eine Erklärung des gesamten Verfahrens . det(A n )=det(A T ) (Beweis 4. Nächste » + 0 Daumen.Beweisen Sie den Satz über die Eigenschaften von transponierten Matrizen? .

Transponierte Matrix • einfach erklärt · [mit Video]

Determinante einer nxn Matrix . Die erste Zeile der transponierten Matrix entspricht der ersten Spalte der Ausgangsmatrix, die zweite Zeile der zweiten Spalte und so weiter.

Matrix transponieren - Studimup.de

Man kann jeder quadratischen (n n)-Matrix A eine reelle Zahl zuordnen, die sogenannte Determinante det A .

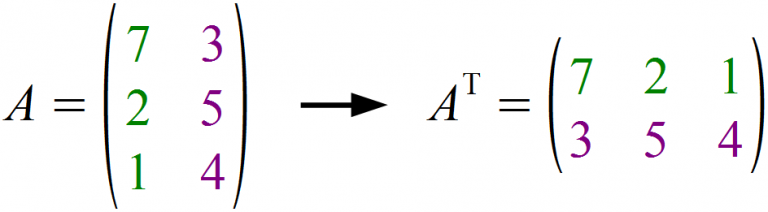
Transponierte Matrix ⇒ einfach und ausführlich erklärt

Sei Det(A)=-1, was ist dann Det(-3A T )? Rechenweg: (-3) 4 det(A T )=. Man erhält sie durch Vertauschen der Zeilen und Spalten einer Ausgangsmatrix.Die Determinante einer Matrix entspricht der Determinante der transponierten Matrix.Die transponierte Matrix $ A^T $ einer Matrix $ A $ erhält man, indem man alle Spaltenvektoren als Zeilenvektoren schreibt. und aus der Tatsache, daß die Determinante von Matrizen mit zwei identischen Zeilen oder zwei identischen Spalten gleich Null ist, ergibt sich nun, daß bzw. Die Determinante der Matrix berechnen, . Hieraus folgt, daß regulär ist, falls , und daß in diesem Fall (14) Next: .Symmetriemuster einer symmetrischen (5×5)-Matrix. Die Eigenwerte der Matrix ¯ müssen ebenfalls nicht alle reell sein, jedoch treten die nicht-reellen Eigenwerte . Du lernst, wie man die Zeilen und Spalten einer Matrix vertauscht und wie sich dies auf die Darstellung der Matrix auswirkt.Orthogonale Matrix: Quadratische Matrix, bei der das Produkt der Matrix und ihrer Transponierten die Einheitsmatrix ergibt. Mit einfachen Beispielen wird dir gezeigt, wie du Matrizen addieren, subtrahieren und multiplizieren kannst.Dies ist ein kostenloser Online-Matrizentransponierungsrechner mit vollständiger, detaillierter, schrittweiser Beschreibung der Lösungen, die Operationen mit Matrizen bis zu einer Größe von 99×99 mit Matrixelementen der folgenden Typen durchführt: Dezimalzahlen, Brüche, komplexe Zahlen, Variablen.Die Determinante einer Matrix A ist eine bestimmte Zahl, die der Matrix zugeordnet wird.comWas bringt das transponieren einer Matrix? – Mathe Boardmatheboard.Eine Matrix wird transponiert, indem man die Matrix an der Hauptdiagonale spiegelt. Entdecke, wie du eine Matrix korrekt transponieren kannst .Linear abhängige Vektoren haben eine Determinante von D = 0; für linear unabhängige Vektoren ist D ≠ 0. Du lernst, was Matrizen sind, wie sie aufgebaut sind und wofür man sie verwendet.Transponierte Matrix : Die Transponierte der Matrix erhältst du durch Vertauschen von Zeilen und Spalten. ? Siehe Determinante im Wiki 1 Antwort + 0 Daumen .Determinante der transponierten Matrix zurück blättern: ‹ Kriterium für invertierbare Matrizen vorwärts blättern: Multiplikationssatz für Determinanten ›

Transponierte Matrix

So bildet die erste .(1) Die Determinante einer Matrix A nist gleich der Determinante ihrer transponierten Matrix AT. Determinanten-Regeln. Für Matrizen, die mehr als 3 Zeilen und Spalten haben, gibt es keine einfache Formel, wie bei kleineren Matrizen. Determinante, 2×2 Matrix (1:19 Minuten) Determinante, 3×3 Matrix, Regel von Sarrus (5:03 Minuten) Determinante, 4×4 Matrix, Laplacescher Entwicklungssatz (6:07 Minuten) Determinante mit dem Taschenrechner berechnen (fx-991DE Plus) (2:51 Minuten) Einige Videos sind leider bis . Eine symmetrische Matrix stimmt demnach mit ihrer transponierten Matrix überein.

Determinante der transponierten Matrix

Determinante einer (4x4)-Matrix Entwicklung nach Laplace - YouTube

Hermitesche Matrix: Definition, Eigenschaften

Matrix transponieren und multiplizieren | Mathelounge

Wenn nicht invertierbar ist, so ist nach Fakt die Determinante und der Rang kleiner als .81 Wie kommt man auf (-3) 4 ? determinante; matrix; algebra; vektoren; Gefragt 10 Mär 2016 von Gast.

NNKJW

XSB