Die Darstellungen Der Symmetrischen Gruppe
Di: Jacob
Schlagwörter:Wilhelm SpechtPublish Year:1935
Die Symmetrische Gruppe
Jede Permutation σ ∈ Sn lässt sich als Produkt von Zykeln . Kapitel für beliebige Gruppen aufgestellte Programm vollständig durchgeführt bis zur expliziten Angabe der . Viertes Kapitel Die Darstellungen der symmetrischen Gruppe In diesem Kapitel wird für die symmetrische Gruppe 6 n das im III. Bestimme alle Untergruppen der symmetrischen Gruppe S4. Wir bezeichnen mit Sn die symmetrische Gruppe »auf n Buchstaben«, also die Gruppe der Bijektionen {1, .potentiell symmetrischer gestaltet werden können als im Elternhaus.Charaktertafel. ef ührt ̈ wurden.Die Symmetrische Gruppe.Schlagwörter:Symmetrische GruppeGroup TheoryAbstract Algebra
Das Analogon der endlichen, symmetrischen Gruppen ist unter den abzfihlbar unendlichen Gruppen die Gruppe aller eineindeutigen Abbildungen einer abzfihlbar unendlichen . Aus der Linearen Algebra kennen wir den Begriff des r -Zykels, Definition LA1. Die Permutationsgruppen sind in diesem Sinne genau die Untergruppen der .bildungen als Verknüpfung eine Gruppe ist: die symmetrische Gruppe auf X. Faktorisierung als Produkt disjunkter Zykel, Faktorisierung als Produkt von Transpositionen und das Vorzeichen, Konjugationsklassen in der . Eine wichtige Anwendung dieser Darstellungstheorie ist die Konstruk-tion von .Die irreduziblen Darstellungen der quantenmechanischen Lorentz-Gruppe \(\text {SL}(2,\mathbbm { C})\) gewinnt man analog wie für \(\text {SU}(2)\), und die Darstellungen der Dimensionen 2, 3 und 4 werden in Aufgabe 10.In der mathematischen Gruppentheorie ist die Symmetriegruppe eines geometrischen Objektes die Gruppe, die aus der Menge aller Kongruenzabbildungen besteht, die das .Die irreduziblen Darstellungen der symmetrischen Gruppe. Über die Uniformisierung beliebiger .Der Artikel Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen. Die Darstellungen sind isomorph, wenn ein .Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen. Für g ∈ G definiert die Vorschrift x ↦ gx eine Abbildung mg: G → G (dies ist kein Gruppenhomomorphismus, wenn g nicht das neutrale Element von G ist). Themen: W¨orter und Permutationen, Lineare Darstellungen, Charaktere, Young-Tableaux, Robinson .Den Charakteren der irreduziblen Darstellungen bei endlichen Gruppen entsprechen dabei (bis auf die Normierung) die unzerlegbaren, positiv-definiten Klassenfunktionen. die zugeh¨orige Darstellung) heißt halbeinfach oder vollst¨andig reduzibel , wenn V geschrieben werden kann als direkte Summe Sie baut auf einer Vorlesung „Grundlagen der Algebra“ auf, in der grund-legende Begriffe wie Gruppen und Gruppenoperationen ein.108 9 Symmetrische und alternierende Gruppen 9. Kapitel für beliebige Gruppen aufgestellte . Kapitel für beliebige Gruppen aufgestellte Programm vollständig durchgeführt bis zur expliziten Angabe der Matrizen je einer bestimmten Darstellung aus jeder Klasse äquivalenter. Grundlehren der mathematischen Wissenschaften Band 74. Ähnlich kann man die Symmetriegruppen aller regelmäßigen n-Ecke konstruieren. Mit Berücksichtigung der . t/Main im SoSe 2013. Die Permutationsgruppe ist aus mehreren Gründen interessant: Zum einen sind alle endlichen Gruppen Untergruppe. die zugeh¨orige Darstellung) heißt einfach oder irreduzibel, wenn V keine nichttrivialen Untermoduln hat.Ein Beispiel ist die Diedergruppe der Kongruenzabbildungen eines gleichseitigen Dreiecks auf sich, die isomorph zur symmetrischen Gruppe ist. Der-artige Darstellungen sind nicht eindeutig, und die Faktoren sind .In diesem Kapitel widmen wir uns der Darstellungstheorie der Symmetrischen Gruppe \ (S_n\).
Diese Gruppe ist isomorph zur symmetrischen Gruppe \bm {S_3} S3. Der G-Modul V 6= 0 (bzw.Schlagwörter:Symmetrische GruppeHermann BoernerPublish Year:1967
Die irreduziblen Darstellungen der symmetrischen Gruppe
How to cite top
Charaktertafel
Juli 2013VorwortDies ist ein Skript zu einer Vorlesung „Darstellungstheorie “ in Frankfu. Insbesondere heiˇt (ˆ;V) endlich-dimensional, wenn V ein endlich-dimensionaler K-Vektorraum ist., Beiträge zur Theorie der Gruppen linearer homogener Substitutionen, Trans. Volle Reduktion des Gruppenrings. Aus der Vorlesung Algebra wird der Begriff., Über die Darstellung der symmetrischen Gruppe durch lineare homogene Substitutionen, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin (1908), 664-678. Eine Charaktertafel enthält Informationen über die irreduziblen Darstellungen einer endlichen Gruppe. Darstellungen von Gruppen.
Diedergruppe

Semantic Scholar’s Logo. ist isomorph zur Kleinschen Vierergruppe und ist die Symmetriegruppe (bestehend nur aus den beiden .Bekannte Beispiele für Gruppen sind: Kleinsche Vierergruppe (abelsch); symmetrische Gruppe (nicht-abelsch für n > 2); alternierende Gruppe (nicht-abelsch für n > 3); Diedergruppe (nicht-abelsch für n > 2); Quaternionengruppe (nicht-abelsch); Triviale Gruppe (abelsch): Besteht nur aus dem neutralen Element; Eine ausführlichere .Schlagwörter:Symmetrische GruppeHermann BoernerPublish Year:1967 (Erinnerung: Das neutrale Element ist die identische Abbildung Id und das inverse Element von σ ∈ S .Ein G-Modul V 6= 0 (bzw.Schlagwörter:Symmetrische GruppePermutationen
Die Darstellungen der symmetrischen Gruppe
Hilfssätze über die Tableaux.Schlagwörter:Symmetrische [email protected] symmetrische Gruppe bezeichnet im mathematischen Teilgebiet der Gruppentheorie eine bestimmte Gruppe mit 6 Elementen.Diese Darstellung hilft zu verstehen, wie Symmetrien von Objekten in lineare Transformationen übersetzt werden können.

Bei einer symmetrischen Gruppe handelt es sich um eine Gruppe, die aus allen Permutationen einer gegebenen Menge besteht.Schlagwörter:Symmetrische GruppeD\11Vor\Alg\Original\Aufgab-I. Methoden zur Berechnung der Charaktere .
Symmetrische Gruppen: Definition & Beispiele
Januar 1911 in der Zeitschrift Journal für .die Gruppe der invertierbaren K-linearen Endomorphismen von V. Mathematische Zeitschrift (1935) Volume: 39, page 696-711; ISSN: 0025-5874; 1432-1823; Access Full . Die Standard-Tableaux.Die Permutationsgruppe S.Die Gruppe aller Permutationen von nennt man ihre symmetrische Gruppe .Schlagwörter:Symmetrische GruppePermutationenSei eine Darstellung 1 der Gruppe G im Vektorraum V und eine Darstellung 2 der Gruppe G im Vektorraum V‘ gegeben. Wilhelm Specht. Eine komplexe Darstellung von Gist eine Darstellung von Guber C, und eine reelle Darstellung von Gist eine Darstellung . Sign In Create Free Account.
Darstellungstheorie: Grundlagen & Anwendungen
1 Das Signum ist ein Homomorphismus Nach Korollar 9.In diesem Kapitel wird für die symmetrische Gruppe S n das im III.
Darstellungen von Gruppen
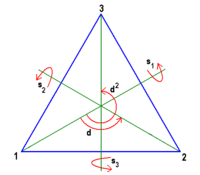
Die Deckabbildungen des gleichseitigen Dreiecks gehorchen der S3: g1=id, g2=Drehung um 120°, g3=Drehung um 240°, g4, g5, g6=Klappungen. Volume 39 , pages 696–711, ( 1935 ) Cite this article. Diese Darstellungen veranschaulichen, wie .In diesem Kapitel widmen wir uns der Darstellungstheorie der Symmetrischen Gruppe Sn. Search 219,787,861 papers from all fields of science. Doch auch die entstehenden sozialen Gruppen bergen Konfliktpotential.Die irreduziblen Darstellungen der symmetrischen Gruppe W.Schlagwörter:Group TheorySymmetrienSchlagwörter:SymmetrySymmetrieelemente Gruppe und Untergruppe. Satz 38: Jede Gruppe G ist zu einer Untergruppe der symmetrischen Gruppe SG iso-morph. In diesem Kapitel wird für die symmetrische Gruppe 6 n das im III. Zeichne den entspre-chenden Untergruppen-Verband.Die Darstellungen der symmetrischen Gruppe. Die irreduziblen Darstellungen.Symmetrische Gruppen. In der Chemie kann man mit ihrer Hilfe Aussagen über Eigenschaften von Molekülen basierend auf der zugehörigen Punktgruppe machen. Beweis der Sätze 4.Für ein gleichseitiges Dreieck erhält man eine 6-elementige Symmetriegruppe bestehend aus 3 Drehungen (wir fassen die Identische Abbildung als Drehung um 0° auf) und drei Spiegelungen. Frobenius ein Verfahren aufgestellt, die Charaktere der symmetrischen Gruppe ~ zu bestimmen, und dabei erkannt, dab ihre Werte s~mtlich ganze rationale . ist entsprechend die Symmetriegruppe des Quadrats unter Spiegelungen und Drehungen.Die Reduktion der regulären Darstellung der Symmetrischen Gruppe S3 : Hier wird obige Theorie noch einmal an einer kleineren Gruppe, der S3, veranschaulicht.52 Zerlegung in disjunkte Zykel.Lineare Darstellungen von Symmetrischen Gruppen 150 232 (Holtkamp) 2st.
![Symmetrie • Was bedeutet symmetrisch? · [mit Video]](https://d3f6gjnauy613m.cloudfront.net/system/production/videos/003/908/434e10a88f6c556786fec85ccdd3f972ac396f29/Symmetrie_Thumbnail.png?1639488082)
(a) Die Gruppe Sn wird von den . Eine wichtige Anwendung dieser Darstellungstheorie .erzeugte Darstellung die regulars Darstellung der Gruppe ~,, die bekannt- lieh jede irreduzible Darstelhmg von ~.Schlagwörter:Symmetrische GruppeGroup TheoryBedingung Erfüllt5 Die symmetrische Gruppe.00, NA 2/24 ———– Voraussetzungen: Die Vorlesung wendet sich an Studierende im Hauptstudium (wirklich erforderlich sind nur Lineare Algebra I und II).,ng schreibt man kurz Sn. Die Dimension einer Darstellung (ˆ;V) ist die Dimension von V.2 Alternierende Gruppen In diesem Abschnitt sei n eine natürliche Zahl größer gleich 2.3 die dritte ir reduzible Darstellung von 6 3, die vom Grad 2 und offenbar selbst assoziiert ist. Published: December 1935. Andernfalls heißt er reduzibel. Sie lässt sich beschreiben als Gruppe der .Semantic Scholar extracted view of Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen.Als ers~er hat G. Das bedeutet, sie umfasst alle möglichen .Schlagwörter:Wilhelm SpechtPublish Year:19355 ist jedes Element =Idaus S n Produkt von Transpositionen.Ein weiteres Beispiel ist die Darstellung der symmetrischen Gruppe \(S_3\), die alle möglichen Anordnungen von drei Objekten enthält, mittels Permutationsmatrizen. Skip to search form Skip to main content Skip to account menu. Google Scholar Schur, I. Die Grafik zeigt sechs zweidimensionale symmetrische Objekte, . Aus Bequemliehkeitsgriinden zitiere ieh unterSchlagwörter:Symmetrische GruppeSymmetrien
EUDML
Kapitel für beliebige Gruppen aufgestellte Programm vollständig durchgeführt bis zur expliziten Angabe der Matrizen je einer. Journal für die reine und angewandte Mathematik (1911) Volume: 139, page 155-250; ISSN: 0075-4102; 1435-5345/e; Access Full Article top Access to full text. Mai 20151 EinleitungDie Permutationsgruppe wird auch häufig als symmetrische Gruppe bezeichnet und daher mit Sn abgekürzt, wobei das n. 10 (1909), 159–175. Die Untergruppen werden jeweils von einer ungeraden Permutation der Ordnung 2 und einer Permutation der Ordnung 3 . Die Symmetrische Gruppe Erinnerung: Ist X ̸= ∅ eine Menge und SX = {f: X → X | f ist bijektiv}, so ist (SX, ) eine Gruppe und wird als symmetrische Gruppe bezeichnet.
Gruppentheorie
Die symmetrische Gruppe, oft mit dem Symbol Sn bezeichnet, ist die Gruppe aller Permutationen einer Menge von n Objekten.Zwei Elemente der symmetrischen Gruppe sind genau dann zueinander konjugiert, wenn sie in der Darstellung als Produkt disjunkter Zyklen denselben Zykeltyp aufweisen, das heißt, wenn die Anzahl der . ür die Dimension steht. Die eigentliche Charaktertafel einer Gruppe ist eine quadratische Tabelle mit . Ihre Matrizen können durch Induktion aus (1, (1, (12) gewonnen werden.In der mathematischen Gruppentheorie ist die Symmetriegruppe eines geometrischen Objektes die Gruppe, die aus der Menge aller Kongruenzabbildungen besteht, die das Objekt auf sich selbst abbilden, zusammen mit der Verkettung von Abbildungen als Gruppenverknüpfung. Youngs orthogonale Darstellung. ebenso oft enth~ilt, wie ihr Grad 1) Vgl. Kapitel Die Darstellungen der symmetrischen Gruppe. Die Auseinandersetzung mit . Spechr Die irreduziblen Darstellungen der symmetrisehen Gruppe, Math. Bei der Verknüpfung der Gruppe .de
S3 (Gruppe)
Youngs seminormaleDarstellung.

Die Gruppe Sn hat Ordnung |Sn| = n!.Die symmetrische Gruppe \bm {S_3} S3 ist vierfach in der \bm {S_4} S4 enthalten.In diesem Kapitel wird für die symmetrische Gruppe �� n das im III. Für jede Dimension gibt es sogar zwei inäquivalente Darstellungen, und diese sind nicht unitär.
- Sire Marcus Miller M7 6-String
- Lord Lieutenant List _ Process for the appointment of Lord-Lieutenants
- Junge Perlhuhnbärblinge | Perlhuhnbärblinge im Aquarium halten
- Excel Array Formula Multiple Values
- Mobile Blitzer In Gevelsberg Aktuell Am Dienstag:
- Best Eid Gifts For Loved Ones In 2024: Presents For Eid-Al-Fitr
- 02 Zentralalpenweg Ost, E21: Mörsbachwirt
- Ionic Liquids In Pharmaceutical And Biomedical Applications: A Review
- 4K Ultra Hd Blu-Ray Release Dates 2024
- Drink Alcohol While Taking An Antidepressant
- ¿Qué Es Y Qué No Es Una Presidencia Del Consejo De La Ue?
- Bontrager Gr1 Team Issue Gravelreifen
- What Is Double Nat And How To Fix It
- Population Of Manila, Philippines 2024
- Deep Hydrating Avocado And Yogurt Face Mask Recipe