Eine Echte Teilmenge Von , Obermengen

Di: Jacob

A muss zumindest alle Elemente von B enthalten und kann auch beliebig viele weitere Elemente enthalten (Hier zum Beispiel 0 und 6).

Teilermenge

Irreflexive Relation

Testen Sie, ob A eine Teilmenge von B ist: = operator, issuperset() Testen Sie, ob A und B disjunkt sind: isdisjoint() Der Set-Typ ist ein veränderlicher Typ, der Elemente hinzufügen und entfernen kann.Eine Menge A heißt echte Teilmenge von der Menge B, wenn A eine Teilmenge von B ist und die beiden Mengen ungleich sind, d.Echte Teilmenge-Symbol Das Echte Teilmenge-Symbol, gekennzeichnet als ⊂, wird in der Mathematik verwendet, um anzuzeigen, dass eine Menge eine echte Teilmenge einer anderen Menge ist, aber nicht gleich dieser. „Wenn alle Elemente der Menge A auch Elemente der Menge B sind, so sagen wir: A ist in B enthalten, A ist eine Teilmenge von B, eine Menge unter B, oder B enthält A, B ist eine Menge über A. die Menge B muss auf jeden Fall zusätzliche . Wir bringen dies durch eine der beiden Formeln. Die Relation „ist Teilmenge von“ bildet eine Halbordnung.Eine Menge A heißt Teilmenge von B (Symbol: A B), wenn jedes Element von A auch in B liegt.Die Schreibweise A ⊂ B bedeutet, dass $A$ eine Teilmenge von $B$ ist. Der Begriff Menge geht auf Bernard Bolzano und Georg Cantor zurück. Ist ein Modell, so ist offenbar = ():= {;} eine Theorie. Gilt für Mengen X, Y, daß X ⊊ Y und X ≠ Y, so nennt man X eine echte Teilmenge von Y. Denn es handelt sich doch um eine echte Teilmenge. M ⊂ N: ⇔ (M ⊂ N) ∧ (M ≠ N) Den ersten Teil der obenstehenden „Hieroglyphen“ kennst du ja bereits: M ist .

Ist {1,1,2,3} eine Teilmenge von {1,2,3,4}?

Die leere Menge ist eine (echte) Teilmenge von jeder Menge und jede Menge ist eine (unechte) Teilmenge von sich selbst. Eine Menge M 1 ist eine echte Teilmenge einer Menge M 2 (ist in M 2 echt enthalten), wenn M 1 eine Teilmenge von M 2 ist, beide Mengen aber verschieden .

Teilmenge einer Menge

der Analysis, der Geometrie .

Zeifen dass ein Körper und ob echte teilmenge | Mathelounge

Die leere Menge gilt immer als Teilmenge jeder anderen Menge.

Menge (Mathematik)

Wir wollen die Behauptung durch einen Widerspruch beweisen. Es handelt sich bei der echten Teilmengenbeziehung um eine strenge Halbordnung.Teilmenge – echte Teilmenge. Hierbei gibt es zwei Möglichkeiten: heißt echte Teilmenge von , . Die Bezeichnung Teilmenge ist dadurch gerechtfertigt, dass jedes Element aus M H M_H M H auch Element von M M M ist. Man sagt auch: $A$ ist echte Teilmenge von $B$.Unter einer Theorie versteht man eine echte Teilmenge von Sätzen einer Sprache der Prädikatenlogik erster Stufe, die bezüglich der Folgerungsrelation (deduktiv) abgeschlossen ist, das heißt, aus folgt bereits für alle Sätze der Sprache. Dazu stehen hier Beispiele.

Grundbegriffe der Mengenlehre

Mengenlehre online lernen

Teilmenge und echter Teilmenge: Eine Menge B ist dann .Mengenlehre: einfach erklärt Zeichen Teilmenge Schnittmenge Vereinigung Formeln Axiome StudySmarter Original

Mengenlehre

Für keine Menge $A$ gilt $A \subset A$.

echte Teilmenge

Das ist genau dann der Fall, wenn sowohl A B als auch B A gilt. Und das trifft oven zu, denn $$\mathbb{R}^2 = \begin{pmatrix} v_1\\v_2\\0 \end{pmatrix} \subset \begin{pmatrix} v_1\\v_2\\v_3 \end{pmatrix} = \mathbb{R}^3 $$ wobei $v_{1,2,3} \in \mathbb{R}$ sind. Die gesamte heutige Mathematik ist auf der Mengenlehre aufgebaut.Ist es nicht, denn 1 und 1 sind zwar gleich, aber doch zwei Elemente A ist eine Teilmenge von B und B ist eine Obermenge von A, wenn jedes Element von A auch in B enthalten ist.

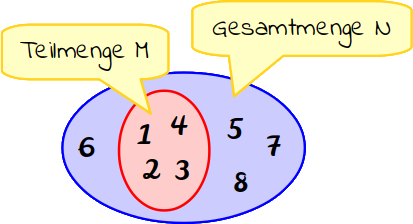
echte Teilmenge | mathetreff-online

B heißt dann Obermenge von A.Weil eine (echte) Teilmenge T von einer Menge X ist die Menge T die Elemente aus X enthält aber nicht alle Elemente aus X enthält. Sie ist Teilmenge jeder Menge. Um eine Teilmenge zu bilden, wählt man einfach einige oder alle Elemente aus der ursprünglichen Menge aus und bildet damit eine neue Menge. Sal erklärt den Unterschied zwischen einer Untermenge, einer strikten Untermenge und einer Obermenge. Und du kennst ja auch schon bereits: die Gesamtmenge M ist gleich der Teilmenge N (M hat also die gleichen Elemente wie N).echte Teilmenge. Die Menge der rationalen Zahlen ist eine echte Teilmenge der Menge der reellen Zahlen.Wenn A A keine echte Teilmenge von C C, aber andererseits nach Voraussetzung gilt A \subset C A ⊂ C, dann muss A=C A = C sein. Name des Gesetzes . Wenn sich viele Menschen an einem Ort befinden, spricht man von einer Menschenmenge. Zur Menge A gehören allerdings noch weitere Elemente.Echte Teilmenge.Teilermenge einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen! Statt Н und К werden manchmal die Symbole М und Й .Menge, die in einer anderen Menge enthalten ist, ohne mit dieser identisch zu sein. Man nennt eine Theorie vollständig, wenn sie für jeden Satz . Und du kennst ja auch . Erinnere dich, dass die Elemente einer Menge alles Mögliche sein können (Tiere, Zahlen, . Das kleine Dach (∧) bedeutet »und«, also existiert noch eine Bedingung für das Teilmengen-sein. Man spricht von einer echten Inklusion, falls eine echte Teilmenge von ist, das heißt, wenn es Elemente in gibt.Enthält B noch mindestens ein Element, das in A nicht enthalten ist, nennt man A eine echte Teilmenge. Um anzugeben, dass das Element $x$ nicht in der Menge $X$ enthalten ist, oder dass $A$ keine (echte) Teilmenge von $B$ ist, benutzt man dieselben Symbole, jedoch durchgestrichen: x ∉ X, A ⊄ B.Eine Teilmenge heißt eigentliche oder echte Teilmenge, falls A A A und B B B nicht die gleichen Mengen sind, falls also A ⊆ B A \subseteq B A ⊆ B und A ≠ B A\ne B A = B ist.eine echte Teilmenge von«, also M ist eine echte Teilmenge von N. Befinden sich viele Äpfel an einem Ort, spricht man von einer .Wenn eine Menge Teilmenge einer anderen ist und die beiden Mengen voneinander verschieden sind, spricht man von einer echten Teilmenge.Ist B eine Teilmenge von A, so ist A eine Obermenge von B. Beispiel: Die graden Zahlen .

Teilmenge

Eines können wir aber hier schon sagen: wäre eine komische Menge! Wir erinnern uns an das Abstraktionsprinzip, . Die (echte) Teilmengenbeziehung $\subset$ ist irreflexiv.Teilmenge, echte Teilmenge und Obermenge. Das kleine Dach (∧) bedeutet »und«, also existiert noch eine Bedingung für das echte-Teilmengen-sein.Für Mengen und mit ist die Inklusionsabbildung : durch die Abbildungsvorschrift =gegeben. $\left( {A \subset B} \right)$ Beispiel: A = {2, 5, 7, 8, 9, 11} und B = {2, 5, 8} direkt ins Video springen Teilmenge. Also grafisch dargestellt quasi ein großer Kreis, in dem ein kleiner Kreis ist und in diesem Kreis sind die Elemente der Menge A = {1,2}, welches eine Teilmenge von B =, {1,2} ist.Beziehungen Zwischen Mengen

Teilmenge

Die Aufgabe: Sei A={2,3,4,5} a) Zeigen sie, dass A keine Teilmenge von B={x | x N und x ist ungerade} ist b) Zeigen sie, dass A eine echte Teilmenge von . direkt ins Video springen Teilmenge A von B.Zu diesem Schluss kommt ein Team der TUM, das erstmals systematisch untersucht hat, ob diese Form der Künstlichen Intelligenz (KI) für den Klinikalltag geeignet wäre. Im Fall mathematischer Strukturen ist die so .Echte Teilmenge: Eine Menge A ist eine echte Teilmenge einer Menge B, bezeichnet mit $A \subset B$, wenn jedes Element von A auch ein Element von B ist und B mindestens .

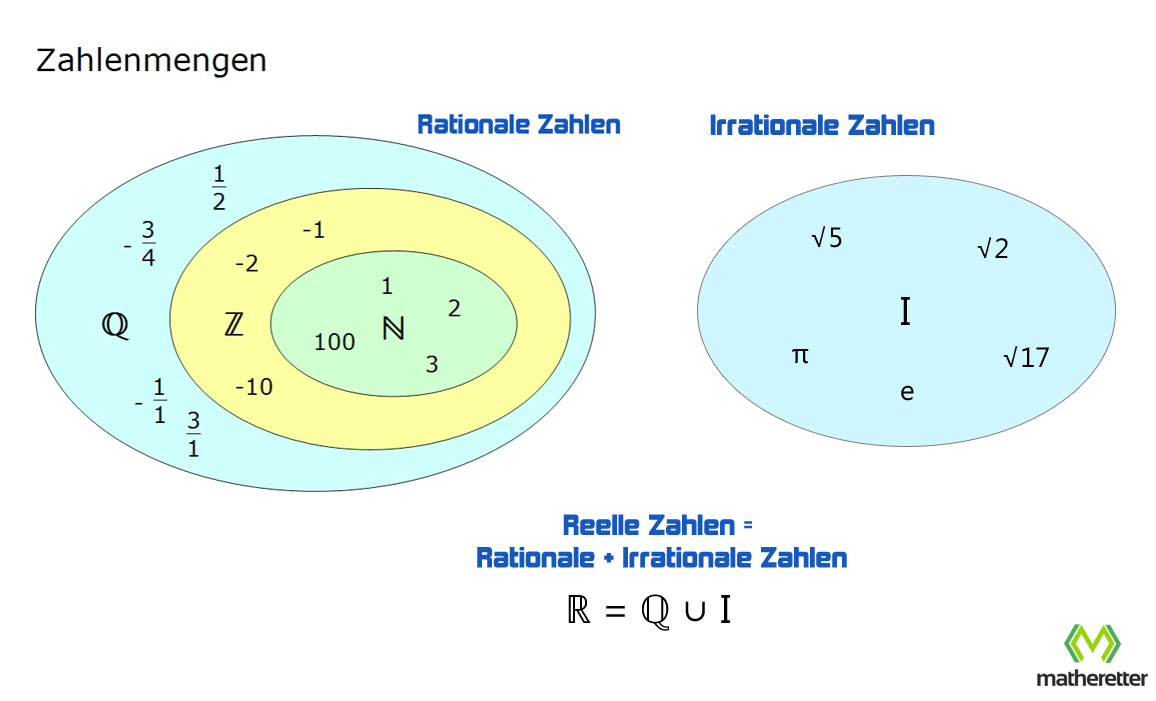
Reelle Zahlen - Matheretter

Die Menge M wird manchmal auch Obermenge . So ist zum Beispiel A eine echte Teilmenge von N, da A № N ist.Die leere Menge ist Teilmenge einer jeden Menge.Eine Teilmenge heißt eigentlich oder echt, wenn weiterhin A ≠ B \mathrm A\neq\mathrm B A = B gilt.

Teilmenge und echte Teilmenge

zum Ausdruck; wobei die Zeichen ⊂ und ⊃ an die üblichen . Der Begriff Obermenge ist somit das korrespondierende Gegenstück zum Begriff Teilmenge . Die Menge aller Teilmengen von einer Menge bezeichnet man als Potenzmenge der betreffenden Menge. ist echte Teilmenge von (oder ist echte Obermenge von ), wenn Teilmenge von ist, aber von verschieden, also jedes Element aus auch Element von ist, aber (mindestens) ein Element in existiert, das nicht in enthalten ist.Spricht man von einer echten Teilmenge, so darf T nicht alle Elemente von M enthalten: Die Operatoren ⊆ und ⊂ sind in dieser Hinsicht vergleichbar mit ≤ (kleiner-gleich) und < . In diesem Fall besitzt B .

Obermengen

Meine Frage: Ich besuche grade für mein Studium ein Vorlesung zu Grammatiken und Automaten. Eine Menge A heißt echte Teilmenge von der Menge B, wenn A eine Teilmenge von B ist und die beiden Mengen ungleich sind, d. ∋ ∋ ∋ U+220B: Enthält-als-Element-Symbol Zeigt an, dass eine Menge das folgende Element enthält.

echte Teilmenge

Es handelt sich bei Menge B um eine echte Teilmenge der Menge A, wenn alle Elemente aus B auch in A enthalten sind. Man unterscheidet aber weiters auch noch zwischen.Sind alle Elemente der Menge auch Elemente der Menge , so ist eine Teilmenge von , in Kurzschreibweise . Leider habe ich zur Zeit schon bei den einfachsten Aufgaben meine Problemchen. Beispiel: 7 ∈ ℕ 7 . Die leere Menge (Symbol: ) enthält keine Elemente.a ist echte Teilmenge von b, . für Schnittmengen. A geschnitten B ist in diesem Fall also die gesamte Menge B: A ∩ B = {2, 5, 8} . Ebenso, wenn C C keine echte Teilmenge .

www.mathefragen.de - (Echte) Teilmenge Schreibweise (Formel?)

Bei einer Website habe ich gelernt, dass A = {1,2} eine Teilmenge von B = {1,2} ist.Es ist wichtig zu beachten, dass die Reihenfolge der Elemente in der Teilmenge keine Rolle spielt und dass jedes Element nur einmal in der Teilmenge . die Menge B muss auf jeden Fall zusätzliche Elemente enthalten, die nicht in A sind.also wenn jedes Element von A auch Element von B ist und umgekehrt.0 Weiß einer von euch ob es falsch ist, wenn man schreibt: {xyz} ist Teilmenge von {zxy}.

Echte Teilmenge

Um das eigens hervorzuheben, kann man dann statt A B auch A $ B schreiben. Er erklärt auch die . Wir nehmen also an, dass $ A $ keine echte Teilmenge von $ B $ ist und dass $ B $ keine echte Teilmenge von $ C $ ist. Manchmal wird das spezielle Pfeilsymbol zur Kennzeichnung benutzt und man schreibt dann :. A ⊆ B oder B ⊇ A . Sie findet Anwendung in vielen Teilgebieten der Mathematik, wie z.Man sagt M H M_H M H ist eine Teilmenge von M M M und schreibt M H ⊆ M M_H\subseteq M M H ⊆ M.Original von BOT2.Warum heißt die Allklasse nicht Allmenge?Weil wir nicht sicher sind, dass sie wirklich eine Menge ist! Von Mengen erwarten wir bestimmte Eigenschaften, die wir im Kapitel „Axiomatische Mengenlehre“ näher kennen lernen werden.Wenn und Mengen sind und jedes Element von auch ein Element von ist, nennt man eine Teilmenge oder Untermenge von : Umgekehrt nennt man die Obermenge von genau . Also grafisch dargestellt . Ist es richtig ein solches Mengenverhältniss mit dem Zeichen ist Teilmenge von zu bezeichnen. In Bolzanos Manuskripten aus den Jahren zwischen 1830 und 1848 heißt es: „Inbegriffe nun, bey welchen auf die Art, wie ihre Theile mit einander verbunden sind, gar nicht geachtet werden soll, an denen somit Alles, was . Ebenso, wenn \( C . Ist A Teilmenge von B und sind A und B verschieden, also A 6= B, so nennt man A eine echte Teilmenge von B.

∈ Element-of Symbol (Element-von-Symbol)

Mengenlehre

Die Menge der Primzahlen ist eine echte Teilmenge der Menge der natürlichen Zahlen.es gibt in der Mengenlehre ja Teilmengen und echte Teilmengen. Für irreflexive Relationen gelten unter anderem die folgenden . Für die folgenden Gesetze sind A, B, C Teilmengen der Grundmenge G. M ⊂ N: ⇔ (M ⊂ N) ∧ (M ≠ N) Den ersten Teil der obenstehenden „Hieroglyphen“ kennst du ja bereits: M ist eine echte Teil-menge von N. (Denn es gibt – zumindest – ein Element von N, das nicht Element von A ist). Der Begriff Teilmenge wurde bereits geklärt.Mengen-Symbole der Mengen-Theorie und Wahrscheinlichkeit mit Name und Definition: Menge, Teilmenge, Vereinigung, Schnittmenge, Element, Kardinalität, leere Menge, natürliche / reelle / komplexe Zahlensatz

Schnittmenge • A geschnitten B

Den ersten Teil der obenstehenden „Hieroglyphen“ kennst du ja bereits: M ist eine Teilmenge von N. Wenn $ A $ keine echte Teilmenge von $ C $, aber andererseits nach Voraussetzung gilt $ A \subset C $, dann muss $ A=C $ sein. Mengen sind niemals eine echte Teilmenge von sich selbst. Python bietet auch den Typ frozenset, der Methoden für Set-Operationen wie set .Menge als gedankliche Zusammenfassung von Objekten. ∌ ∌ U+220C Eine Menge A heißt Teilmenge einer Menge B , wenn jedes Element von A auch zur Menge B gehört: A ⊆ B ⇔ ∀ x ( x ∈ A ⇒ x ∈ B) Die obige Formel bedeutet .

Mengen und Mengenoperationen

Oder ist es nur richtig wenn man schreibt ist echte Teilmenge von. T \subset M T ⊂ M. Wir definieren allgemein: A ⊆ B: ∀ x: x ∈ A x ∈ B A\subseteq B :\iff \forall x: x\in A \implies x\in B A ⊆ B: ∀ x: x ∈ A x ∈ . A ⊂ B meint: A ist eine echte Teilmenge von B wenn A in B enthalten ist, aber nicht identisch ist mit B. Eine Teilmenge heißt echt, wenn sie nicht leer und nicht identisch mit ihrer Grundmenge ist.Die Teilmenge ist ein Thema aus der Mengenlehre.

NNKJW

XSB