NNKJW

XSB

Endlich-Additives Wahrscheinlichkeitsmaß

Di: Jacob

Bei endlichen Zufallsvariablen gibt man die Wahrscheinlichkeitsverteilung oft in tabellarischer Form an. Soweit ich weiß, ist die endgültige Referenz für diese Art von Dingen Howard & Rubins Konsequenzen des Axioms der Wahl, auf die ich mich unten beziehe. für jede endliche Folge von paarweise disjunkten Mengen, , falls , für jede beliebige Folge .Lassen Sie die Schlüssel-, Nachrichten- und Chiffretexträume alle sein $\mathbb{Z}$, die in Bijektion mit ist $\mathbb N$. Sei (Ω,F) ein meßbarer Raum.

mathe einfach erklärt - wahrscheinlichkeitsrechnung 6 - YouTube

Wahrscheinlichkeitsraum

2 Beispiel (0-1-Experiment)

Wahrscheinlichkeitsverteilung

Der Begriff des abzählbar-additiven Wahrscheinlichkeitsmaßes wird in einführenden Darstellungen der Wahrscheinlichkeitstheorie beim Übergang von . Dabei sind \(\Omega \) eine endliche . (P2) Normiertheit: P() = 1 = 100% („sicheres Ereignis“).

1 Maßtheoretische Grundlagen

Endliches Maß

enthält für jedes beliebige .Eine Gruppe G heißt amenabel falls ein endlich additives, links inva-riantes Wahrscheinlichkeitsmaß auf den Teilmengen von G existiert. Bereits der einfachste Fall eines endlichen Ergebnisraums mit .Ein endlicher Wahrscheinlichkeitsraum ist ein Wahrscheinlichkeitsraum, dessen Grundmenge endlich ist und dessen σ-Algebra die Potenzmenge ist. h ([0,∞],B¯+) (S,A) B¯+ ist die von den Intervallen auf [0,∞] erzeugte σ-Algebra (die σ-Algebra der Borel-Mengen auf R¯+ = [0,∞] Die A-B¯+ messbaren h nennen wir auch die nichtnegativen messbaren Funktionen (definiert) auf S. Eine Abbildung P : F → [0,1] heißt Wahrscheinlichkeitsmaß .} ein endlicher oder abzählbar unendlicher Grundraum und P ein Wahrscheinlichkeitsmaß auf Ω. Prinzipiell kann nach dem empirischen Gesetz der großen Zahlen für die .Kurz: µ : A → [0,∞] ist σ-additiv. Gilt P(ω) = 1/|Ω| für alle ω ∈ Ω, so heißt das Wahrscheinlichkeitsmaß P die . Manchmal wird die Wahrscheinlichkeitsverteilung auch Wahrscheinlichkeitsmaß oder Wahrscheinlichkeitsgesetz genannt.

Wahrscheinlichkeit: Einfach erklärt & Beispiele

de

Weitere Eigenschaften von Wahrscheinlichkeitsmaßen

Dann heißt (Ω, P) ein endlicher Wahrscheinlichkeitsraum mit Ergebnisraum Ω und Wahrscheinlichkeitsmaß P. Ebenso kann man ein σ-endliches Maß in ein Wahrscheinlichkeitsmaß . Der Wahrscheinlichkeitsraum ist damit ein mathematisches Modell zur Beschreibung von Zufallsexperimenten.Wahrscheinlichkeiten fordern wir nicht nur die endliche Additivit¨at, sondern die Additivit¨at bez ¨uglich abz ¨ahlbar vieler Ereignisse.Da ein Wahrscheinlichkeitsmaß ist, ist es auch ein lokal endliches Maß.Eine Abbildung der Form heißt Wahrscheinlichkeitsmaß, wenn folgende Eigenschaften („Axiome von Kolmogoroff“) erfüllt sind: Nichtnegativität: Für alle gilt: Normiertheit: Ist , so gilt: Additivität: Für gilt: Die Additivität gilt auch für mehrere Ereignisse , wenn diese paarweise unvereinbar sind, d.Seltener findet sich auch die Bezeichnung Wahrscheinlichkeitsgesetz. Ein Wahrscheinlichkeitsmaß auf A ist ein Maß ρ auf A mit ρ(S) = 1. Die Mengenfunktion hei t Wahrscheinlichkeitsma auf , falls.Der folgende Satz liefert eine Charakterisierung aller endlich-additiven Mengenfunktionen, die sogar Wahrscheinlichkeitsmaße sind. (P1) (,,Normiertheit“) (P2) f r paarweise disjunkte (,, -Additivit t“) Falls ein Messraum und ein . Dies ist die Definition, mit . endlich viele Ereignisse, sondern auch für .Ich werde eine bestimmte Bijektion auswählen, indem ich die nicht-negative Ganzzahl-Zuordnung zu Evens und die negative Ganzzahl-Zuordnung zu Odds mache und lasse $\mu$ sei das asymptotische .#A wenn A endlich ∞ sonst f¨ur A ⊂ Ω.Die Subadditivität von Wahrscheinlichkeitsmaßen, die in Teilaussage 4 von Theorem 2. Wir nennen ein Maß endliches Maß, falls : S![0;1), d. A i\A j= Ø, i6= .

Wahrscheinlichkeitsmaß und Zähldichten? (Stochastik, lineare Algebra ...

Endlich-dimensionale Verteilungen; Existenzsatz von Kolmogorow

Bekanntestes Beispiel von endlichen Maßen sind die Wahrscheinlichkeitsmaße . F¨ur den Urheber der ersten L ¨osung liegt in V4-206 ein namhafter Schokoriegel bereit. Sie ist essentiell für den modernen axiomatischen Aufbau der Stochastik sowie der Maß- und Integrationstheorie, wird jedoch von manchen . Gemeinsam mit der mathematischen Statistik, die anhand von Beobachtungen zufälliger Vorgänge Aussagen .Die σ-Algebra besteht aus den Ereignissen, denen das Wahrscheinlichkeitsmaß Zahlen zwischen und zuordnet.

Grundlagen der Wahrscheinlichkeitsrechnung/Einführung in die ...

; Dann stimmen die endlich-dimensionalen Verteilungen des ,,Koordinaten-Prozesses“ , der gegeben ist durch für beliebige und , mit den Wahrscheinlichkeitsmaßen überein.Die Wahrscheinlichkeitstheorie, auch Wahrscheinlichkeitsrechnung oder Probabilistik, ist ein Teilgebiet der Mathematik, das aus der Formalisierung, der Modellierung und der Untersuchung von Zufallsgeschehen hervorgegangen ist.Übersicht

Grundbegriffe

Maß (Mathematik)

Jedes Prämaß ist auch ein Inhalt.Email: [email protected] der bedingten Wahrscheinlichkeit für endliche Wahrscheinlichkeitsräume/Beweise. Dabei ist die Grundgesamtheit Ω nicht leer und die Mengen an Ereignissen sind Teilmengen der Grundgesamtheit.

abzählbar-additives Wahrscheinlichkeitsmaß

Seien Ω = {ω 1, ω 2, .

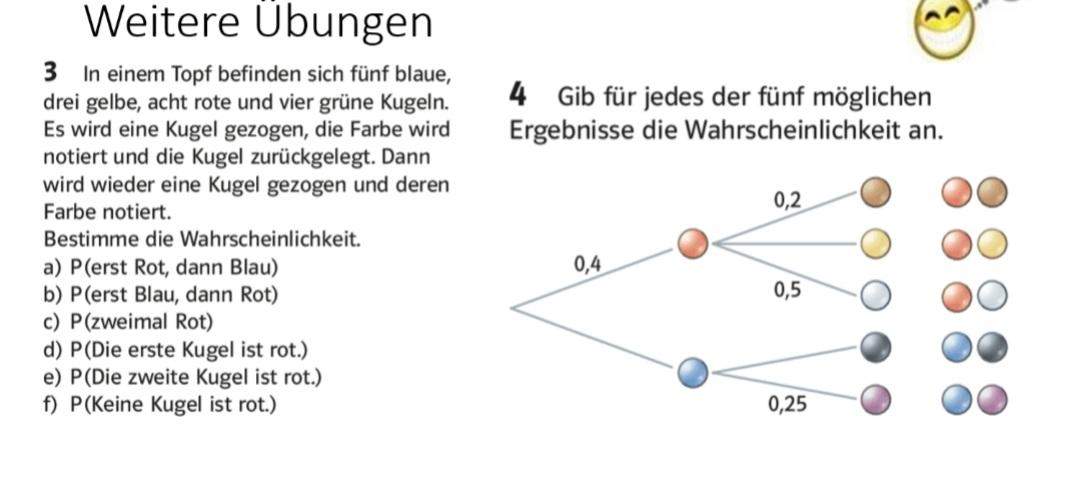
Wie geht das mit der Wahrscheinlichkeit? (Schule, Mathematik, 10. Klasse)

(P1) Nicht-Negativität: P(A) 0 .(ii) is˙ additiv.Anmerkung 3: Schw¨acht man die zweite Bedingung auf endliche Vereinigungen ab , wird F eine Algebra genannt. Im ersten Abschnitt definieren wir Wahrscheinlichkeitsräume sowie diskrete und kontinuierliche Verteilungen und geben die wichtigsten Verteilungen als Beispiele an.; ist eine σ-Algebra über der Grundmenge , also eine Menge bestehend aus Teilmengen von , die enthält .Ein endlicher Wahrscheinlichkeitsraum (kurz: W-Raum, engl.In diesem Kapitel wird das Kolmogorovsche Axiomensystem für den Fall endlicher Grundräume vorgestellt und der Begriff der Wahrscheinlichkeit formal-logisch definiert. (A) <1für alle A2S. Ist Ω endlich, #Ω = n, so k¨onnen wir µ zu einem Wahrscheinlichkeits .Ihre Elemente heißen Ergebnisse. Die Zahl wird dabei als . fur jede Folge .Ein endliches Maß ist ein Begriff aus der Maßtheorie, einem Teilgebiet der Mathematik, das sich mit abstrahierten Volumenbegriffen beschäftigt.Jedes endliche Maß, welches nicht das Null-Maß ist, kann durch Normierung in ein Wahrscheinlichkeitsmaß umgewandelt werden.

Wahrscheinlichkeitsmaß

Wahrscheinlichkeitsinhalt

Wahrscheinlichkeitsmaße dienen dazu, Mengen eine Zahl . Im Einzelnen bedeutet das: ist eine beliebige nichtleere Menge, genannt die Ergebnismenge. f¨ur alle ϕ,ψ∈ . Beispiele, bei denen man die Zuordnung mit festen Formel ermitteln kann: Binomialverteilung (diskrete .

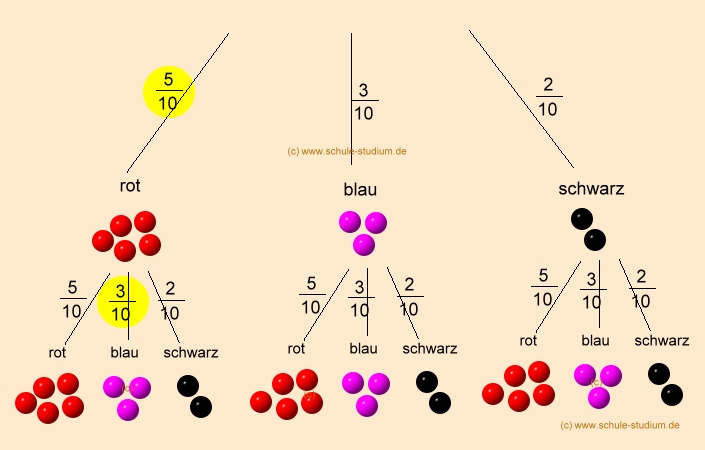
Wahrscheinlichkeitsrechnung (Stochastik). Urnenproblem anschaulich erklärt.

Das Wahrscheinlichkeitsmaß ist eine der wichtigsten Definitionen, damit wir überhaupt mit Wahrscheinlichkeiten rec. Eine Funktion : S![0;+1] heißtInhalt(oderendlich-additivesMaß),falls (i) (;) = 0 (ii) .Ein Wahrscheinlichkeitsmaß P auf einer ˙-Algebra Aüber einem Ergebnisraum 6= ? ist eine Abbildung P : A!R mit den folgenden Eigenschaften.endlich-additives nichtatomares Wahrscheinlichkeitsmaß bewertet. Die Nichtnegativität sowie () = gilt per Definition, die endliche Additivität erhalten wir aus der -Additivität indem wir ab einem bestimmten .

Wahrscheinlichkeitsmaß

Anschaulich ist ein endliches Maß ein Volumenbegriff, bei dem die betrachtete Grundmenge nur ein endliches Volumen besitzt. fur alle¨ A ∈ F ist Pr A = 1− Pr(A) 2.Definition (Inhalt/endlich-additives Maß). Dann heißt (Ω, P) diskreter Wahrscheinlichkeitsraum .

Bedingte Wahrscheinlichkeit - einfach erklärt! · Studyflix

Eine Funktion : S![0;+1] heißtInhalt(oderendlich .Wahrscheinlichkeitsmaß P in einem Wahrscheinlichkeitsraum (Ω, \({\mathfrak{A}}\), P) derart, daß es endlich oder abzählbar unendlich.Definition

Kapitel 8 Probabilistische und Possibilistische Logik

Als Wahrscheinlichkeit bezeichnet man ein Maß für das Eintreten eines Ereignisses .Ein Wahrscheinlichkeitsraum ist ein Maßraum (,,), dessen Maß ein Wahrscheinlichkeitsmaß ist. Dieses Maß heißt Z¨ahlmaß auf Ω. Gilt P (ω) = 1/|Ω| für alle ω ∈ Ω, so heißt das . (P1) Nicht-Negativität: P(A) 0 8A2A. Wintersemester 2013/2014 Maß- und Integrationstheorie . 2 Definition (Inhalt/endlich-additives Maß).Die Wahrscheinlichkeit als Teil der Grundlagen der Wahrscheinlichkeitsrechnung liefert Dir beispielsweise eine Antwort auf die Frage, wie sicher Du beim nächsten Würfelspiel . Ohne diese erweiterte Forde-rung w¨urde man nur eine sehr ” armselige“ Theorie erhalten. Sei M eine nichtleere Menge und S ein System von Teilmengen von M mit ;2S. Außerdem finde keine Kommunikation ” außerhalb“ des Algorithmus statt.2 wird das Konzept der Zufallsvariable eingeführt und die .endlich-additive Wahrscheinlichkeitsmaße Definition Ein endlich-additives Wahrscheinlichkeitsmaß ist eine Abbildung P : B → [0,1] mit 1.Eine Funktion P, die jeder Teilmenge A einer endlichen (Ergebnis-)Menge Ω eine reelle Zahl P (A) zuordnet, heißt Wahrscheinlichkeitsverteilung (Wahrscheinlichkeitsfunktion oder auch Wahrscheinlichkeitsmaß), wenn sie folgenden drei Bedingungen genügt: Axiom 1 (Nichtnegativität) P (A) ≥ 0; Axiom 2 (Normiertheit) P (Ω) = 1; Axiom 3 .In diesem Kapitel geben wir einen Überblick über die Grundbegriffe der Wahrscheinlichkeitstheorie.; Mit Techniken der Maßtheorie kann man zeigen, dass es ein (eindeutig bestimmtes) Wahrscheinlichkeitsmaß gibt, für das für beliebige und sowie gilt.Wie lassen sich Grenzpunkte einer Menge endlich additiver Wahrscheinlichkeitsmaße beschreiben? 1 aduh 2020-09-14 14:47. (P3) ˙-Additivität: Für jede Folge (A n) n2N mit A n 2A, n 2N, von paarweise disjunkten Mengen (d.: probability space) ist ein Paar \((\Omega , \mathbb {P})\).Die σ-Additivität, manchmal auch abzählbare Additivität genannt, ist in der Stochastik und in der Maßtheorie eine Eigenschaft von Funktionen, die auf Mengensystemen definiert sind, deren Argumente also Mengen sind.(Der Satz von Hahn-Banach lautet im Buch Form 52. Jeder endliche . Aus dem Axiomensystem resultierende Regeln wie die Monotonie oder die Subadditivität eines Wahrscheinlichkeitsmaßes und Additionsgesetz bilden das kleine . In Verallgemeinerung der 3. Dann ist µ ein Maß auf (Ω,P(Ω).Ist die Abbildung von nicht negativen Funktionen auf ihre endlich additiven Integrale halbkontinuierlich?

σ-Additivität

Dann stimmen die .1 betrachtet wurde, gilt nicht nur für zwei bzw. Definition: Ein Wahrscheinlichkeitsraum (Ω,F,Pr) besteht aus einer Ergebnismenge Ω, einer σ-Algebra F ¨uber Ω und einem Wahrscheinlichkeitsmaß Pr : F → [0,1] mit: 1. h ([0,∞],B¯+) .

Stochastik, leicht erklärt

wenn für gilt.Mathe Nachhilfe im Online Kurs: Stochastik.Die Mengenfunktion heißt Wahrscheinlichkeitsmaß auf , falls (P1) (,,Normiertheit“) (P2) für paarweise disjunkte .

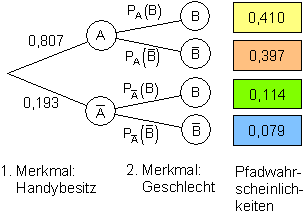
Bedingte Wahrscheinlichkeit • Mathe-Brinkmann

Sei R ein Ring in einer Menge und phi eine endlich-additive ...

Ich frage mich, weil, wenn das Netz konvergiert, es verwendet werden kann, um ein endlich additives Wahrscheinlichkeitsmaß zu definieren $\mu$ an $2^{\mathcal X}$ durch $$\mu(X) = \lim_{\mathcal F} \mu_F(X).Diese Frage bezieht sich auf einige Äquivalente des Hahn-Banach-Theorems in $\textsf{ZF}$ Mengenlehre. Teilaussage von Theorem 2. Vorschl¨age f ¨ur sch ¨one neue Aufgaben werdenDefinition (endlicher Wahrscheinlichkeitsraum) Sei Ω eine endliche nichtleere Menge, und sei P : Ω → [ 0, 1 ] ⊆ ℝ eine Funktion mit ∑  ω ∈ Ω P(ω) = Dann heißt (Ω, P) ein endlicher Wahrscheinlichkeitsraum mit Ergebnisraum Ω und Wahrscheinlichkeitsmaß P.Seminar Facetten der Geometrischen Gruppentheorie FølnerDefinitionderamenablenGruppen David Dyschelmann 21.) Die ’Aufgabe der Woche’ ist eine inoffizielle Belustigung. Wenn X {\displaystyle X} ein topologischer Hausdorff-Raum mit seiner Borel σ {\displaystyle \sigma } -Algebra ist, dann erfüllt δ x {\displaystyle \delta _{x}} die Bedingung, ein inneres reguläres Maß zu sein, da Singleton-Mengen wie { x } {\displaystyle \{x\}} immer kompakt sind.Ein Wahrscheinlichkeitsmaß, kurz W-Maß oder synonym [1] Wahrscheinlichkeitsverteilung beziehungsweise kurz W-Verteilung oder einfach Verteilung genannt, ist ein grundlegendes Konstrukt der Stochastik.das Wahrscheinlichkeitsmaß P; Alle dieser drei Komponenten sind der Bestandteil des Wahrscheinlichkeitsraum.Mit Techniken der Ma theorie kann man zeigen, dass es ein (eindeutig bestimmtes) Wahrscheinlichkeitsma gibt, f r das f r beliebige und sowie gilt.Dort werden Wahrscheinlichkeitsmaße verwendet, um zufälligen Ereignissen, die als Teilmengen eines Ergebnisraums aufgefasst werden, Wahrscheinlichkeiten zuzuordnen.