Fourier-Reihe Einer Sägezahnfunktion
Di: Jacob
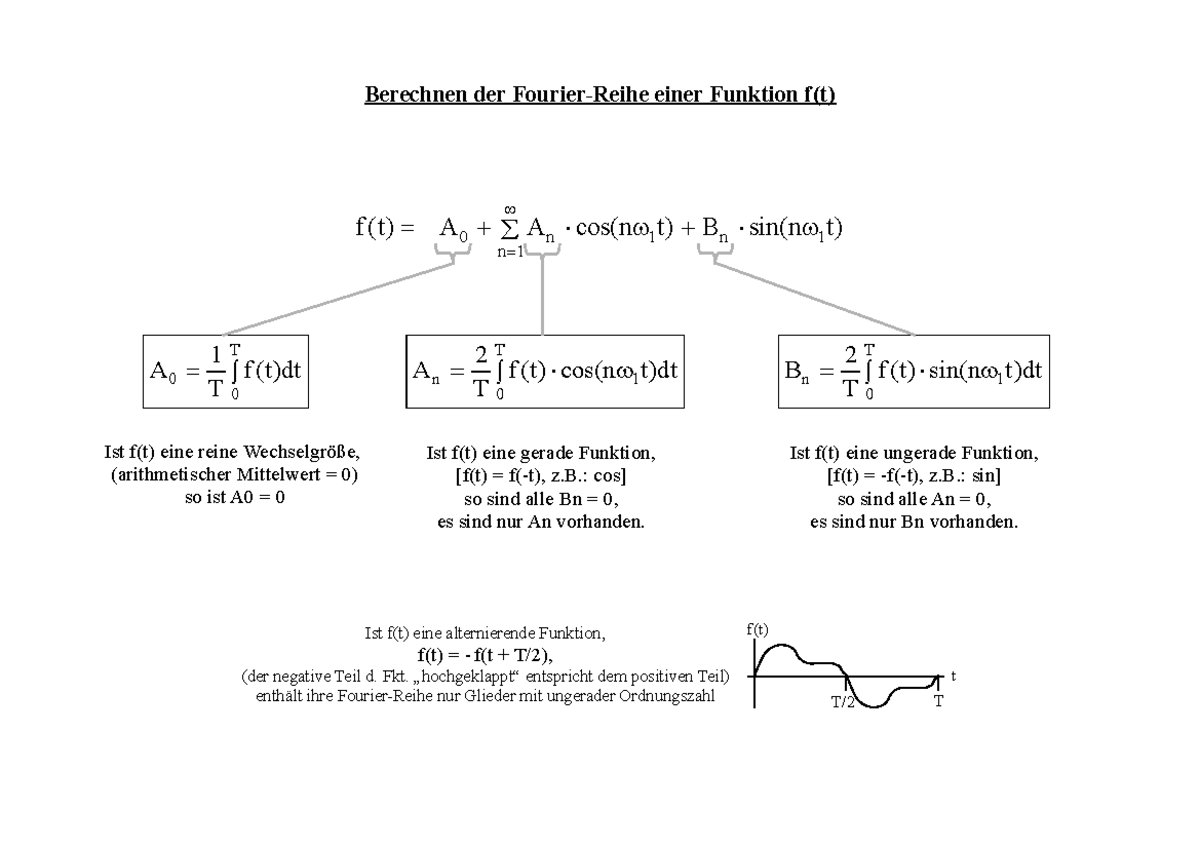
to/2kJoYo4 Mathematik in 5 Minuten https://go. Partielle Integration liefert: bk = 1 2π * 0 2π (π− x) sin(kx) dx = 1 2π(x − π k . Schreibweise: f(t) ˘ 1P k=1 keik!t: Satz (10.Fourier-Reihe der Sägezahnfunktion.Fourierreihe, Sägezahnfunktion entwickeln Universität / Fachhochschule Folgen und Reihen Tags: Fourierreihe . Kapitel 8: Fourier-ReihenVorlesung Höhere Mathematik für. Für setzen wir die Funktionen und fest durch bzw.1K views 6 years ago.gl/t2oUiuTop Lehrbuch für Fourier https://amzn.600 11 Fourier-Reihen Beispiel 11. Die Funktion t→sin(t) hat Perioden 2πn, aber keine mit sgemeinsam: Ihre Summe ist nicht periodisch!Die App veranschaulicht die Ermittlung der Fourier-Reihe (blau) der Sägezahnfunktion f (gelb). 6 in Teil 2 an.8) gegeben, so nden wir die Amplitude aus Periodenlänge: 2 π. Die Funktion läßt sich damit für alle t bestimmen, indem die Funktion auf diesem Grundintervall einfach -periodisch wiederholt wird.6) punktweise . Es sei nun die -periodische Funktion, die für durch . Dirichlet und Riemann vermuteten, dass dies insbesondere für stetige Funktion gelte, bis .Joseph Fourier. In obiger De nition wird f identi ziert mit der T{periodischen Fortsetzung von f (direkte Fortsetzung). Außerdem setzen wir .
Fourier-Reihen: Sägezahnfunktion
Bewege hierzu den weißen Schieberegler, um die Frequenz der in f enthaltenen harmonischen (Sinus-)Schwingung (weiß) einzustellen, deren Amplitude („Lautstärke“) ermittelt werden soll („auf die gehört werden soll“).Die Fourierreihe konvergiert an einer Unstetigkeitsstelle \(t_{u}\) gegen das arithmetische Mittel aus dem rechts- und linksseitigen Grenzwert der Zeitfunktion f(t): .Fourier-Reihe von 2-Pi-periodischen Funktionen Fourier-Reihe der -periodischen Funktion auf , wobei das Grundperiodizitätsintervall ist und abkürzend für steht.Beispiel 3: Die Fourier-Reihe einer Sägezahnfunktion Sei f : R → R die 2π-periodische Funktion mit f(0) = 0 und f(x) = π− x 2 für alle xP]0, 2π[.Die Fourierreihen bereiten dir noch Probleme? Im Folgenden zeigen wir dir, wie du Fourierreihen bildest und erklären dir an einem einfachen Beispiel wie du sie anwendest.Die mittlere Stromstärke einer Sägezahnspannung beträgt die Hälfte des Scheitelwertes I 0, die effektive Stromstärke beträgt . in Wobbel-Generatoren zur Pr ufung von Ger aten .Arbeitsauftrag Das Applet zeigt die Fourier-Analyse für eine Kippschwingung (Sägezahnschwingung).2 (Periode p=2π) Für die Bestimmung der Fourier-Koeffizienten gemäß (11.
Kapitel H Fourier
Verwandte Vide. estrelladelanoche.
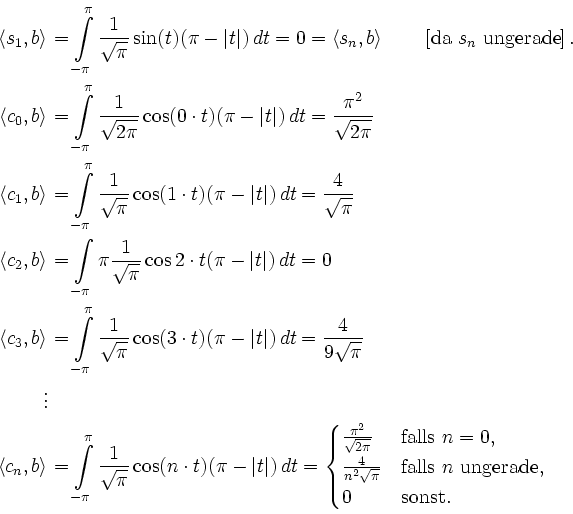
Erklärung Fourierreihen: Trigonometrische Reihe Fourierreihe Beispiel 308 views 2 years ago SAARLAND UNIVERSITY. Wir bestimmen die Fourier-Reihe FS (f) in .Fourier-Reihe und Fourier-Integral.31K subscribers.Links auf diese Seite; Änderungen an verlinkten Seiten; Datei hochladen; Spezialseiten; Permanenter Link; Seiteninformationen; Seite zitieren; Gekürzte URL abrufenheiˇt die Fourier{Reihe von f. Die Fourier–Analyse hat wichtige technische Anwendungen: Datenanalyse, Mustererkennung, z.Sägezahnspannung, Kippspannung, eine elektrische Wechselspannung, die periodisch linear ansteigt und dann instantan auf den Ausgangswert abfällt (siehe Abb. Gegeben sind zwei T . April 2018 Zusammenfassung Der S agezahn wird als Funktion z. In der reellen Fourier-Reihe von f verschwinden wieder alle Kosinus-Koeffizienten, da f ungerade ist. Ich möchte die Sägezahnfunktion in Excel graphisch .About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket Press Copyright .Die Basisfunktionen der Fourierreihe bilden ein bekanntes Beispiel für eine Orthonormalbasis.4 dargestellte periodische Funktion mit der Periode p=2π f(x)= 0 für −π ≤x ≤0 sinx für 0 ≤x ≤π ist die Fourier-Reihe zu bestimmen (Maple-Lösung auf Seite 851).Autor: Sciencebarbie erklärt MathematikFourier Reihen Beispiel 1 (Sägezahnfunktion) – YouTube.

Berechne die Fourierreihe der -periodischen ,,Sägezahnfunktion„, welche durch definiert ist für .

Sägezahnfunktion Fourierreihe Sägezahn
Während für periodische Funktionen zu den diskreten Frequenzen die Amplitude gehört, ergibt sich für nicht-periodische Funktionen eine Amplituden-Funktion in Abhängigkeit der . Berechne die Fourierreihe der -periodischen ,,Sägezahnfunktion„, welche durch definiert ist für . Zu einer Frequenz erhält man zwei Koeffizienten, a und b , da die Summanden in der Fourierdarstellung die Überlagerung von jeweils zwei harmonischen Sinus- und Kosinusschwingungen gleicher Frequenz darstellen.Beispiel 1: Die Fourier-Reihe einer Zackenfunktion. Als Fourierreihe, nach Joseph Fourier (1768–1830), bezeichnet man die Reihenentwicklung einer periodischen, abschnittsweise stetigen Funktion in eine Funktionenreihe aus Sinus- und Kosinusfunktionen.Fourier Reihe – Sägezahn Hallo liebe Community, ich rätsle schon den halben Tag und hoffe Ihr könnt mir bei meinen Problem weiterhelfen.
Fourierreihen
Video ansehen7:54Hier werden systematisch und leicht verständlich die Koeffizienten der Fourier-Reihe einer ungeraden, 2π-periodischen Funktion berechnet.6K subscribers.
Fourierreihen: Einf uhrung
Ein Beispiel einer Fourier-Reihe ist die Sägezahnfunktion,
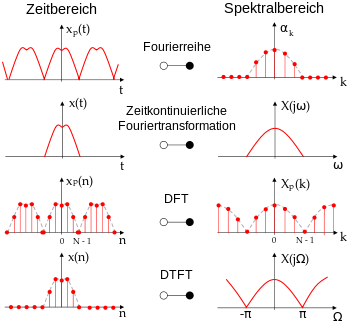
FourierReihe in spektraler Darstellung
Sägezahnspannung: Zeitlicher Verlauf. Roland Speicher.der W armeausbreitung in Festk orpern uns stieˇ dabei auf einen L osungsansatz mit trigonometrischen Reihen (Fourier-Reihen). Akademie Raddy. Berechnen Sie die Koeffizienten der Fourierreihe. Untersuche zudem die Fourierreihe im Intervall auf Konvergenz und bestimme . Ist eine harmonische Schwingung in der Form (1.Schauen wir uns noch die Sägezahnfunktion aus Abb.Fourierreihen: Einf uhrung 3 errechnen. Gegebene Punkte: A(0/1), B(π /0) und C(2 π /-1) Mein Lösungsweg: a0=0 Flächenteile .Die Frage nach hinreichenden Bedingungen für die Konvergenz einer Fourier-Reihe besitzt eine lange Tradition innerhalb der Mathematik.4) wird r =−L . ausdrücken oder mit der um den .FourierReihe in spektraler Darstellung f t .Playlist: https://www. Dafür wurde die Diskrete Fourier-Transformation . Aus entnehmen wir die Werte der ersten vier Koeffizienten zu b 1 = 2, b 2 = –1, b 3 = 2/3 und b 4 = –1/2. Inhaltsübersicht.Fourier–Entwicklung der Sägezahnfunktion Das Konvergenz-Kriterium von Dirichlet Fourier–Entwicklung von Treppenfunktionen 3 Rechenregeln zu Integration und Glattheit Integrieren und Differenzieren Abklingen der Fourier–Koeffizienten Von Potenzreihen zu Fourier–Reihen 4 Fazit: Fourier–Analyse periodischer Funktionen Zusammenfassung . In formaler Hinsicht sind das die gleichen Beziehungen, mit denen wir die karte-sischen Koordinaten eines Punktes in der Ebene durch seine Polarkoordinaten ausdr ucken 4.0:00 Sägezahnfunktion 0:23 Darstellung Fourierreihe und -koeffizienten 0:47 Keine geraden Anteile 2:12 Ungerade Anteile 4:01 erste paar Summanden 4:30 Plot .Video ansehen5:06Fourier Videos in der Playlist https://goo.
Fourierreihen
Im Rahmen der Theorie der .Wie eine große Klasse periodischer Funktionen lässt sich dieser Sägezahnverlauf in einer dazu gleichwertigen Darstellung mittels Fourierreihe.
Fourier Reihe
Dirichlet klärte 1829 die grundlegenden Fragen zur Konvergenz. Sinusglieder an = 0Wir stellen im Folgenden die wichtigsten dieser Regeln zusammen: Sätze und Regeln zu Fourierkoeffizienten bzw.Fourierreihe verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Periodische Funktionen können als (additive) Überlagerung von Sinus- und Kosinusfunktionen beliebig genau approximiert werden.com/watch?v=U0DepaaCRRs&list=PLdFyJ_aaUnWZFBSjl3nEuofdfRfbNo_8eLehrgang zur Symmetrie von Funktionen:http://www.

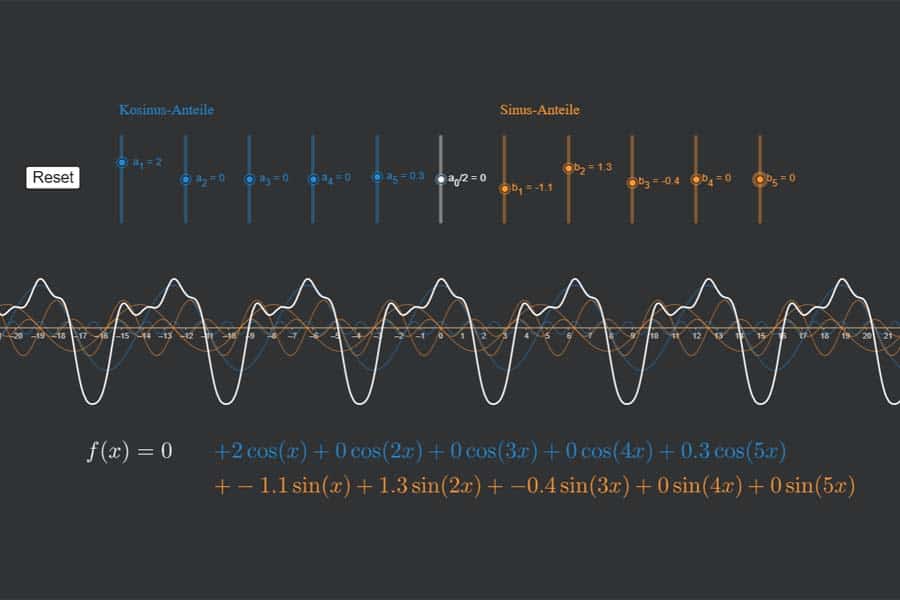
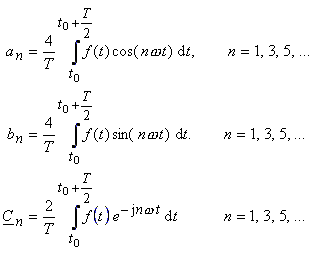
Aufgabenstellung : Fourierreihe einer Sägezahnfunktion entwickeln.Fouriertransformation einer Sägezahnfunktion.Fourier Videos in der Playlist https://goo.Die Fourierreihe (reell) für die Dreiecksschwingung (achsensymmetrisch) der Periodendauer 2Pi wird berechnet.Aufgabe 1: Fourierreihe einer Sägezahnfunktion¶ Die Sägezahnfunktion ist gegeben durch die periodische Fortsetzung von \(f(x) = x\) für \(-\pi \leq x < \pi\) .1 Grundlegende Begri e Joseph Fourier: Jede\ periodische Funktion l asst sich durch ei-ne Uberlagerung\ von Grundschwingungen cos(!t);sin(!t) und zugeh origen Oberschwingungen .Eine Funktion mittels trigonometrischer Funktionen darzustellen ist das Ziel bei Fourierreihenentwicklung.Aufgabe 355: Fourier-Reihe und Reihenwert Aufgabe 357: Sinus- und Kosinus-Reihe von sin² Aufgabe 371: Fourier-Reihe und Reihenwert Aufgabe 735: Orthogonalität von Sinus und Kosinus Aufgabe 736: Fourier-Reihe eines quadratischen Polynoms, Reihenwert Aufgabe 737: Fourier-Entwicklungen von trigonometrischen Funktionen (2 Varianten) Sei f : ℝ → ℝ die 2π-periodische Funktion mit.Fourier-Reihe eines S agezahn Emil Obermayr, DD3AH 29. Dazu müssen wir nur die Berechnung der Messwerte durch % das Signal sn = pi/2 - pi/2*tn; % .
Fourierreihe einer Sägezahnkurve
Autor: Elektrotechnik in 5 Minuten by Alexander StögerWie man zu einer geeigneten Funktion die zugehörige Fourierreihe aufstellt, wird hier am konkreten Beispiel einer Sägezahnschwingung erläutert. Teil 1 ist bis zur Berechnung des Fourier-Koeff.Die dargestellt Funktion hat eine Periode von 2π und kann als Fourier-Reihe entwickelt werden: (siehe Applet) Die untere Darstellung zeigt das Amplitudenspektrum der . Die dargestellt Funktion hat eine Periode von 2π und kann als Fourier-Reihe entwickelt werden: (siehe Applet) Die untere Darstellung zeigt das Amplitudenspektrum der Kippschwingung, d. Untersuche zudem die Fourierreihe im Intervall auf Konvergenz .php?title=Sägezahnfunktion/Identität_auf_Einheitsintervall/Fourierreihe/Fakt&oldid=881766“ Fourier war davon überzeugt, dass jede periodische Funktion sich durch ihre Fourier-Reihe darstellen lässt.Abgerufen von „https://de. neben dem konstanten Glied nur Kosinusglieder bn = 0 f −x = f x , f x = a0 2 ∑ n=1 ∞ an⋅cos n x Die Fourier-Reihe einer ungeraden Funktion f (x) enthält nur ungerade Reihenglieder, d. Es gibt einige Anwendungsfälle, in denen die Fourier-Transformation mittels eines Computers berechnet werden soll.Fourier führte im Jahr 1822 die Fourier-Reihe ein, die jedoch nur für periodische Signale definiert ist und zu einem diskreten Frequenzspektrum führt. Ist nach der Amplitude gefragt, mit welcher die Frequenz n im Signal vor- kommt, muss . Playlist: • Fourierreihen 1 Fourieranalyse und .4: Periodische Funktion zu Beispiel 11. (x) = |x| für alle x ∈ [ − π, π ].
Sägezahn Fourierreihe
2: Für die in Bild 11.Beispiel: Die Sägezahnfunktion s(t) = t−⌊t⌋hat Periode n= 1,2,3,. Damit kann die Fourierreihe in einer für manche Zwecke geeigneteren – und vielleicht auch ästetisch ansprechenderen – Form angeschrieben .Die Fourier-Reihe einer geraden Funktion f (x) enthält nur gerade Reihen-glieder, d.
Mathematik-Online-Lexikon: Fourierreihe der Sägezahnfunktion
den relativen Anteil der Amplitude der .Damit ist die Fourierreihe der Sägezahnfunktion bestimmt. Als Fourierreihe einer periodischen Funktion f, die .Wir fragen nach der Konvergenz dieser Fourier-Reihe, nach der Konvergenzge- schwindigkeit und untersuchen, unter welchen Voraussetzungen in (7.
Mathematik-Online-Lexikon: Fourierreihe der Sägezahnfunktion
- Xyfindit Review 2024: Is The Xy4 Tracker Worth It?
- Interaktiver Showroom Von Garamantis
- How To Bottle Flip Like A Pro *New Technique* Haters Will
- Hno-Ärzte In Biberach Und Laupheim
- Unesco-Welterbe In Hessen: 7 Sehenswürdigkeiten
- Windows 10 Mui Language Packs 07 2015
- 27 J.K. Rowling Book Recommendations
- Teletext Schweiz Deutsch – Offizielles Telefonbuch der Schweiz
- Fake-Nachricht: Hallo Mama, Dies Ist Meine Neue Nummer
- Grohe Blue Zubehör Reinigungskartusche 40434001