Homologie Und Kohomologie – Biologie lernen: Homologie und Analogie
Di: Jacob
Als Homologie bezeichnet man in der biologischen Systematik und der vergleichenden Anatomie die grundsätzliche Übereinstimmung von Organen, Organsystemen, . Sie ist noch vielseitiger als die .Merkmale, die einen gleichen Grundbauplan aufgrund eines gemeinsamen Vorfahren besitzen, bezeichnest du als Homologien / homologe Organe.Dieses Lehrbuch erläutert die algebraische Topologie hinter den bahnbrechenden Resultaten von J. Man spricht hier von Verhaltenshomologien.
Homologie
Nicht nur äußere und innere Organe von zwei nah verwandten Lebewesen zeigen einen hohen Grad an Übereinstimmung, sondern auch viele Verhaltensweisen stimmen überein.Die Topologie, wie sie heute verstanden wird, ist ein Kind des 20.1 Einleitung und Motivation ; 2 CW-Komplexe und zelluläre Homologie ; 3 Eilenberg-MacLane-Räume und Moore-Räume ; 4 Faserungen über CW-Komplexen ; 5 Zelluläre Kohomologie und Produkte ; Teil 2 – Spektralsequenzen und das allgemeine Theorem von Serre ; 6 Serre-Spektralsequenzen ; 7 Modulo-C-Klassen und die rationale . Blank Aktuelles Das Kurzskript ist aktualisiert (Version vom 11. Literaturhinweise 1 0.loeh@mathematik. In den davon unabhängigen Kapiteln 9 bis 13 werden Differentialformen und der Satz von Stokes auf Mannigfaltigkeiten behandelt. Doch in der Biologie werden zwei Formen der Ähnlichkeit unterschieden: Homologie und Analogie.Diese und einiges mehr über Differentialformen, Orientierungen und de Rham’sche Kohomologie findet man in [BT], [Sp1, Kapitel 6–8] und [ST]. Insbe-sondere werden wir Produkte in Kohomologie und Dualit atsph anomene studieren und .Die singuläre .Hauptgegenstand des Buches sind Homologie-, Kohomologietheorien und Mannigfaltigkeiten. F ̈ur jedes n = 0, 1, .Methoden der algebraischen Topologie untersucht werden (persistente Homologie) und erschlieˇt v ollig neue M oglichkeiten in Datenanalyse und Mustererkennung (topologische Datenanalyse). Die ersten acht Kapitel geben eine Einführung in die Algebraische Topologie: es werden Begriffe wie Homologie, CW-Komplexe, Produkte und Poincare Dualitäte eingeführt und deren Anwendungen . Beim Schimpansen beobachtet man zum .Kohomologie von R aumen hat die analogen formalen Eigenschaften wie Homologie: Homotopieinvarianz: Homotope stetige Abbildungen induzieren dieselbe Abbildung in .
Kohomologie eines Komplexes
Löh Sommersemester 2013/14 Inhaltsverzeichnis -1. Eine entscheidende Motivation zu ihrer Einführung ist die Poincaré-Dualität, die für eine .
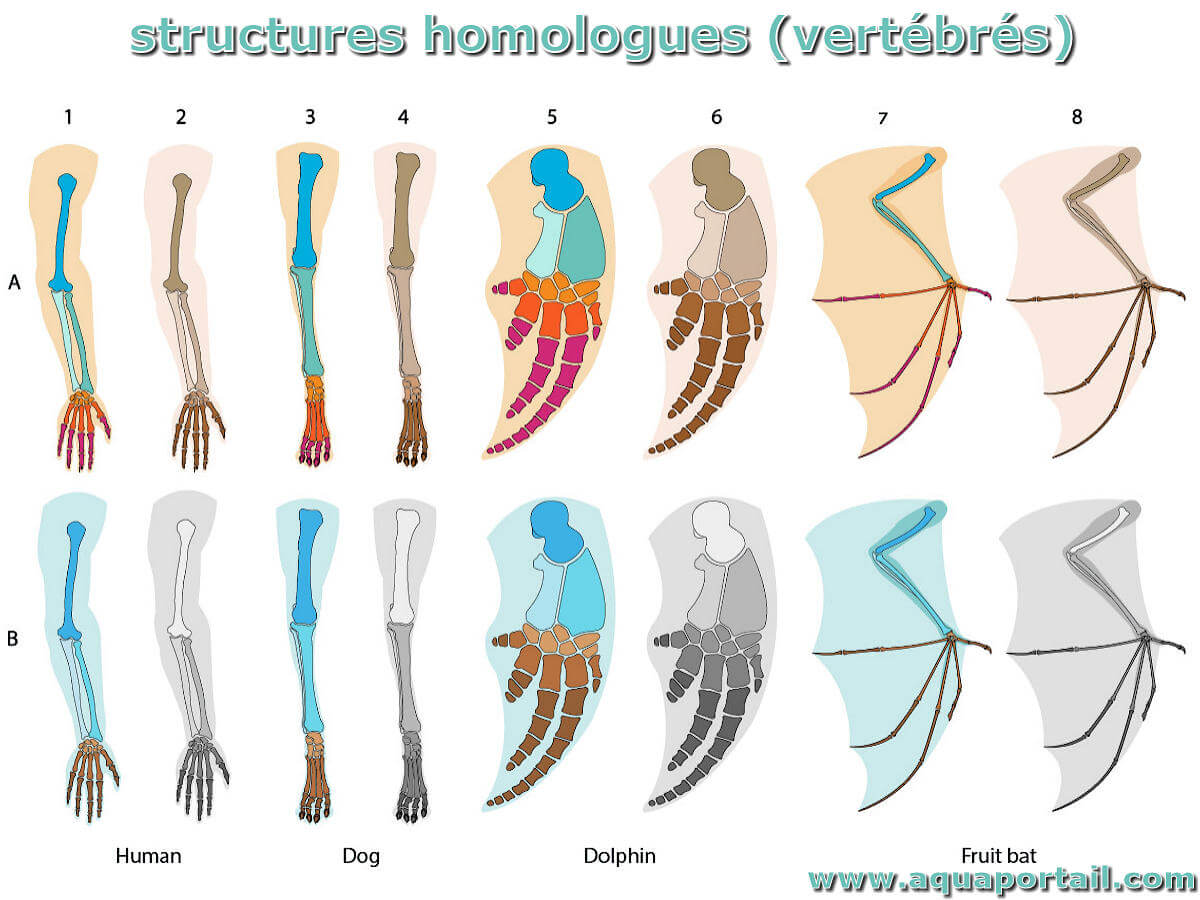
HOMOLOCIE – Homologie = Abstammungsähnlichkeit – homologe Organe, sind Organe die den selben Grundbauplan aufweisen aber bei unterschiedlichen Arten auftreten – können dennoch Unterschiede in der Funktion & im äußeren Bau aufweisen – Ursache sind unterschiedliche Lebensräume – divergente Entwicklung Kriterium der Lage .Ein Lesebuch von den elementaren Grundlagen bis zur Homologie und Kohomologie.Homologie und Kohomologie. Erhalte Online-Nachhilfeunterricht von geprüften Nachhilfelehrern mithilfe digitaler Medien über Notebook, PC, Tablet oder Smartphone. Online-Nachhilfe. Grundlagen, singuläre Homologie und Kohomologie (Teil II) Simon Hüsken [GM] Kapitel I. Die in Kapitel 14 und 15 behandelte de Rham .Homologiekriterien. ist der Gruppe G in funktorieller Weise eine abelsche . April 2020) De nition von Homologie und Kohomologie mit Koe zienten .Er ist Professor für Mathematik und Informatik an der Hochschule der Medien in Stuttgart. Die Homologie ist eine allgemeine mathematische Technik verwendet , um das Hindernis zu messen , die bestimmten Suiten von morphisms sein genau. Konkreter sollen in der Vorlesung Homologie und Kohomologie fur topologi- sche R aume de niert und untersucht werden. Download book PDF. In diesem Seminar wollen wir de Rham-Kohomologie . Direkt zum Inhalt Homologie und Homotopie – eine Wiederholung. Beide Gruppen sind Untergruppen von (;).Vortrag im Seminar ” Homologische Algebra“ Simpliziale und singul¨are Homologie Matthias Nagel Wintersemester 2008/09 Ein einf¨uhrendes Beispiel
Homologien
Simpliziale und singul¨are Homologie
Vor allem die Kohomologie ist ein Werkzeug, das in fast allen geometrischen Disziplinen eine grundlegende Rolle spielt. Authors: Fridtjof Toenniessen. Kohomologie Axiomatische Kohomologie Singuläre Kohomologie Zelluläre Kohomologie Klassifikation von Kohomologietheorien Produkte auf . Wie die Algebra ist die Topologie als universelle Sprache für weite Teile der Mathematik grundlegend geworden. Kohomologiegruppen induzieren.Kohomologie ist eine in gewissem Sinne duale Theorie zur Homologie. Groˇen Wert ist auf die Mitarbeit im Seminar zu legen, weshalb auch An-wesenheit wichtig ist.:Aufbau des Herzens ist bei fast allen Säugetieren identisch; Aufbau .Algebraische Topologie III– (Ko)Homologie: Dualität und Produkte, SS 2014 Prof.Es ist in vielen Bereichen wie der Algebra, der algebraischen Topologie, der algebraischen Geometrie und der . Die Grundidee dabei ist, dass wirDie Kohomologie ermöglicht es, komplexe Fragen nach der Struktur von Varietäten zu beantworten und bietet Einblicke in die Zusammenhänge zwischen verschiedenen .

Bei Mannigfaltigkeiten gibt es noch einen weiteren Zusammenhang zwischen Kohomologie und Homologie, der tiefliegende geometrisch-topologische Eigenschaften dieser Räume beschreibt, den Poincaréschen Dualitätssatz. Um ihren Eindeutigkeitssatz genau zu .Homologien und Verhalten. Einführung 3 1.Homologie und Kohomologie Frage 1. 14 Vortr age (1) Homologie und Kohomologie mod 2. Wendet man auf einen Kettenkomplex C den Kofunktor Hom (− ; G) an (wobei G eine feste abelsche Gruppe .Homologie 1) Übereinstimmung des Handelns mit der Vernunft und damit – nach der stoischen Lehre – mit der Natur. Serre über höhere Homotopiegruppen der Sphären. Sei C ein Kettenkomplex und A eine abelsche Gruppe. Warum sind die Eigenschaften(a)-(e)interessant? Um diese Frage zu beantworten, brauchen wir erst einige .Ähnlichkeiten aus der vergleichenden Biologie in der Gestalt (Morphologie), dem inneren Bau (Anatomie), im Stoffwechsel (Biochemie) oder im Erbgut (Genetik) werden als Belege für die Verwandtschaft und die Evolution der Organismen herangezogen. Sie ist noch vielseitiger als die Homologie und hat im 20. Der dritte Grund liegt in der Allgemeinheit dieses Konzepts. Jahrhundert Querverbindungen in fast alle Bereiche der reinen Mathematik entwickelt, zum.
Andriy Haydys und Martin Callies
Dies ist ein neues und modernes Lehrbuch über Topologie. Eine entscheidende Motivation zu ihrer Einführung ist die Poincaré-Dualität, die für eine geschlossene n-dimensionale Mannigfaltigkeit besagt, dass ihre p-te Homologie isomorph zu ihrer (n-p)-ten Kohomologie ist (siehe Kapitel 8).

Homologie und Analogie in Biologie
Dual bezieht sich auch darauf, dass . Hauptgegenstand des Buches sind Homologie-, Kohomologietheorien und Mannigfaltigkeiten. Eine -Kokette heißt Kozykel, falls = gilt, und Korand, falls ein (;) mit = existiert. Im Folgenden wird mit (;) die Gruppe der Kozykel und mit (;) die Gruppe der Koränder bezeichnet. Um eine Homologie beweisen zu können, wurden Homologiekriterien aufgestellt, wovon mindestens eins erkannt werden muss: Kriterium der Lage: beschreibt, dass einzelne Strukturen stets in gleicher Lage im komplexen Gefüge anderer Strukturen liegen (Bsp.10 Kohomologie und die Poincaé-Dä In diesem Kapitel wollen wir die Homologie ausbauen und die dazu passende duale Theorie besprechen, die Kohomologie.Trotz ihrer Ähnlichkeiten haben sich die Flügel von Flugsaurier (1), Fledertieren (2) und Vögeln (3) unabhängig voneinander entwickelt und stellen somit ein analoges Organ dar.Die singuläre Kohomologie ist nun die Kohomologie bezüglich des singulären Kokettenkomplexes.Was diese Überlegung mit Homologie und Analogie zu tun hat, wirst du in diesem Beitrag von Biologie lernen erfahren. Der Kokettenkomplex Hom(C,A) von Cmit Koeffizienten in Aist definiert durch Hom(C,A)n= Hom Ab(C n,A) . Diese erfreuen sich besonderer struktureller Eigenschaften: Homotopieinvarianz, lange exakte Homologiesequenz, Additivität, Ausschneidung. Im gleichen Verlag sind von ihm erschienen Das Geheimnis der transzendenten Zahlen – Eine etwas andere Einführung in die Mathematik und Topologie – Eine Einführung von den elementaren Grundlagen bis zur Homologie und Kohomologie. Berechne die Euler-Charakteristik für die getwisteten Strukturgarben auf dem projektiven Raum über einem algebraisch abgeschlossenen Körper . Beliebte Inhalte aus . Lernen in gewohnter Umgebung Qualifizierte Nachhilfelehrer Alle .Der zweite Grund dafür, dass Homologie und Kohomologie wichtig sind, liegt darin, dass Abbildungen zwischen Räumen immer Abbildungen auf ihren Homologie- bzw.1 Algebraische Topologie III (Ko)Homologie: Dualität und Produkte im SS 2014 Kurzskript Prof. 2) Ähnlichkeiten bei Lebewesen,.In den ersten acht Kapiteln werden Begriffe wie Homologie, CW-Komplexe, Produkte und Poincaré Dualität eingeführt und deren Anwendungen diskutiert. Die klassischen Integralformeln aus der Vektoranalysis, so wie sie in der Physik eingesetzt werden, sind Spezialfälle der Integralformel von Stokes 3.; Falls Sie eine mündliche Prüfung über Algebraische Topologie III ablegen möchten, wenden Sie sich bitte per email an clara. Die mengentheoretische Topologie verdankt wie die Cantorsche .
Homologietheorie
Zentral für die Feststellung einer Homologie ist die Übereinstimmung oder Ähnlichkeit eines Merkmals in der räumlichen und gegebenenfalls zeitlichen Struktur (Verhalten, . Mit Hilfe dessen können weitere Invarianten definiert und untersucht werden.Weitere Beispiele sind die heute fast vergessene Vietoris-Homologie und auf der Kohomologieseite die Čech-Kohomologie.
Kohomologie
Dopheide [GM] Kap.Hochschild Homology and De Rham Cohomology of Stratifolds – heiDOK. CW-Homologie, Homotopiegruppen.In diesem Video lernst du, den Unterschied zwischen Homologie und Analogie zu verstehen. Wir erklären dir, wie sich diese Begriffe in der Biologie unterscheiden und welche Bedeutung sie haben.
![Homologe Chromosomen • Bau und Funktion · [mit Video]](https://d1g9li960vagp7.cloudfront.net/wp-content/uploads/2020/11/Homologe_Chromosomen_WP-1024x576.jpg)
Diese kann man als .Übersicht
Kohomologie: Grundlagen & Anwendungen
Dies gilt vor allem für angeborenes Verhalten. Analoge Organe sind Organe die zwar die selbe Funktion haben, ihren Ursprung jedoch nicht in einem gemeinsamen Vorfahren, sondern durch ähnlichen Umweltbedingungen, . Tauche ein in die Welt der Evolutionsbiologie und erweitere dein Wissen darüber, wie Lebewesen miteinander verwandt sind. Eilenberg und Steenrod wollten diese Theorien auf eine gemeinsame Basis stellen und zeigen, dass sie auf einer großen Klasse von Räumen die gleichen Gruppen ausrechnen.Homologie und Kohomologie Für gleichnamige Artikel siehe Homologie. Ein Beispiel sind die . Sie führen jedoch unterschiedliche Funktionen aus.
Die Homotopie der Sphären
Das Homologisieren ist ein allgemeines .Kohomologietheorien und ihre Interaktion mit Homologietheorien betrachten.Übersicht
Hochschild-Homologie und Kohomologie
Ewald, Christian-Oliver.Homologie Definition.In diesem Kapitel wollen wir die Homologie ausbauen und die dazu passende duale Theorie besprechen, die Kohomologie. Name, Vorname (7.Die Vortr age m ussen mindestens 2 Wochen vor dem Vortragstermin fertig und mit mir durchgesprochen sein. Homologie bedeutet, dass Merkmale ähnlich sind, da sie einen gemeinsamen Grundbauplan haben. Grundlagen, singuläre Homologie und Kohomologie (Teil I) Simon Hüsken [GM] Kapitel I.Zum Beispiel, mit Hilfe von Homologiegruppen kann man beweisen, dass jede stetige Abbildung vom abgeschlossenen Ball in einem Euklidischen Raum in sich selbst einen . Zwecks leichterer Berechenbarkeit werden wir Homologiegruppen einführen und in einigen wichtigen Beispielen berechnen.Dieses Seminar ist eine Einf ̈uhrung in Homologie- und Kohomologietheorie einer diskreten Gruppe G.
Kohomologie von Gruppen
<< | Kurs:Bündel, . Jahrhunderts und umfaßt eine ganze Reihe von Gebieten. Blatt 14 ist online (freiwillige Abgabe).Homolog ie forschung, bedient sich einer vergleichenden Betrachtungsweise unter Anwendung der Homologiekriterien. Jahrhundert Querverbindungen in fast alle Bereiche der reinen Mathematik entwickelt, zum Beispiel in die Analysis oder die .

German Title: Hochschild Homologie und De Rham Kohomologie von . Die ersten acht Kapitel geben eine Einführung in die Algebraische .
Biologie lernen: Homologie und Analogie
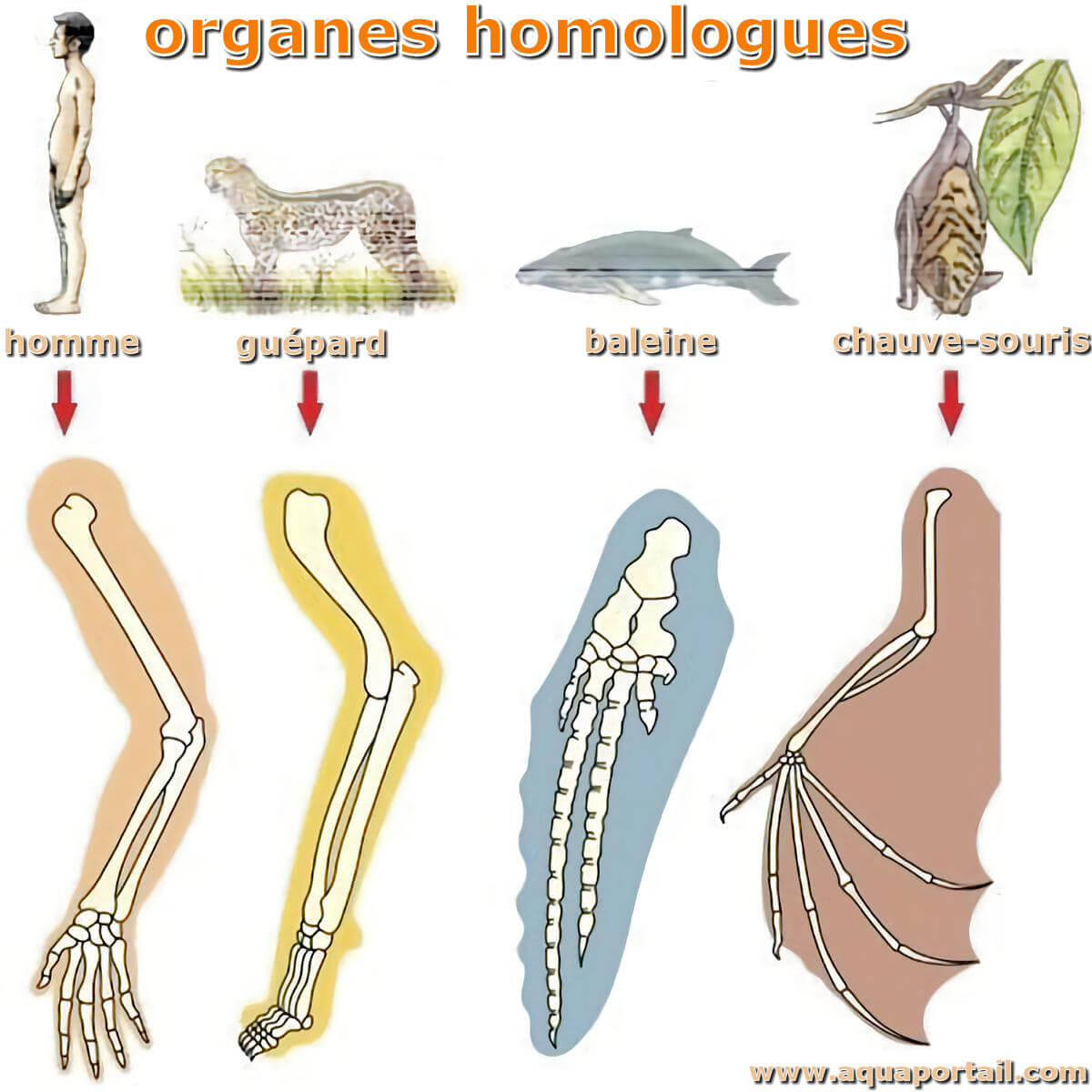
Homologieforschung
Homologie (Biologie)
- White Lies: Why Telling Little Fibs Can Be A Big Deal
- Rodeway Inn Near Venice Beach | Rodeway Inn near Venice Beach
- 7 Propiedades De Los Cacahuetes Para La Salud
- Hartz 4 Verlängerung 2024 – Ein-Euro-Job für Arbeitslose: Dürfen Sie ablehnen?
- Warren Buffet’S 2024 Strategy, What’S He Buying And
- Zierapfel Red Juvel – Zierapfelbäume kaufen?
- Bayerische Landesbrandversicherung Ag Gesch.St. In Deggendorf
- Wie Lange Muss Fimo Backen? 7 Tipps Für Perfekte Ergebnisse
- Neue Brillengläser Kosten : ️ Brille Krankenkasse » Das zahlt die Krankenkasse ab [2024]?
- Aktiensparen: Wie Sie Aus 87 Euro Monatlich 1.000 Euro Extra-Rente
- Klüngelskerl Melodie Pdf | Klüngelskerle
- 43 Y/O Mtf Breast Augmentation W/No Hormones
- Delock Aktives Displayport 1.2 Zu Hdmi Kabel 4K 60 Hz 2 M
- Kalbsnuss Rezept Portwein _ Video: Saftige Kalbsnuss dank Niedergarmethode