NNKJW

XSB

Integral Rotationskörper Durch Substitution Lösen

Di: Jacob

Integration durch trigonometrische Substitution ist ein Sonderfall der Integration durch Substitution.

Integration durch Substitution

Sigmaregeln und Konfidenzintervalle.

Integration durch Substitution bei unbestimmten Integralen

Beachten Sie, dass man konstante Faktoren aus dem Integral herausziehen darf (Distributivgesetz). Hier ein paar Integrale, die per Substitution lösbar sind. Volumen von Rotationskörper um die x-Achse « existiert bereits.Das komplette Video findest du auf http://bit. Die Substituion wählen. AB: Einführung in das Integrieren mit linearer Substitution. Um den Rechenweg zu sehen, einfach auf das entsprechende Integral klicken.Integral Rotationskörper durch Substitution lösen.Ermitteln Sie die Mantelfläche des entstandenen Rotationskörpers im Bereich 0 ≤ x ≤ 12.1 Berechnung des Volumen eines Zylinders. In diesem Fall muss das Integral in zwei Integrale mit jeweils einer kritischen Grenze aufgeteilt werden: Wir beginnen damit, das erste uneigentliche Integral. Gegeben sei ein bestimmtes Integral ∫ 0 2 2 x e x 2 d x, welches integriert werden soll. Anmerkung: Da Funktionen üblicher Weise als y=f (x) gegeben . Dabei versucht man durch Substitution (Ersetzen eines Ausdrucks . Video: Textaufgaben 4: Mittelwert einer Funktion.Machen Sie sich anhand der Animation klar, wie man die (Volumen-)Integralformel für Rotationskörper durch Nährung mit Zylinderscheiben erhält.

Integration durch Substitution

Integration durch Substitution • einfach erklärt · [mit Video]

Ich versuche zurzeit diese Aufgabe zu lösen : Das im Intervall 0,Pi unter der Kurve mit der Gleichung f(x) = sinx liegende Flächenstück rotiere um die x-Achse. Es sei y=f (x) eine über dem Intervall [ a,b] stetige Funktion.

Integral Rotationskörper mit Substitutionsregel | Mathelounge

ly/R23bGvDieser Film zeigt Dir gut verständlich, wie Du die Substitutionsregel beim Integrieren anwenden kannst. Gleichung aus Schritt 2 ableiten. n stehen die Integrationsgrenzen fest. Diese Regeln musst du beim Integrieren beachten, genau wie beim Ableiten von Funktionen: Name.) Ersetze die kritische Intervallgrenze durch eine Variable : 2. zur Stelle im Video springen. Berechnen Sie das .Ein Zylinder entsteht durch die Rotation einer konstanten Funktion f (x) = c (in diesem Beispiel f (x) = 3) um die x-Achse. Gefragt 11 Mär von Bauing. Aufgaben und Erklärungsvideos für Mathe der Klassen 9, 10,11, 12 und 13.

10 Integration durch Substitution

rotationskörper; volumen; rotationsvolumen; integral + 0 Daumen.Integration durch Substitution: Lösungen der Aufgaben; Aufgabe 1: Integriere durch Substitution. Aufgabe 1540: Unbestimmtes und bestimmtes Integral rationaler Funktionen mit Grad (3,2) und (1,2) Interaktive Aufgaben: Interaktive Aufgabe 88: Koeffizientenbestimmung für ein Polynom, Extremwerte und . Das folgende Beispiel soll dies näher verdeutlichen. Die lineare Substitution kann widerum nur dann angewandt werden, wenn eine Funktion mit einer linearen Funktion verkettet ist.Das Volumen sieht ähnlich wie ein Kegel, bei deem dies durch die Berechnung des Umfangs der Grundfläche mal die Höhe berechnet wird. Arbeitsblätter für LehrerInnen.Rotationskörper wird in der Geometrie ein Körper genannt, dessen Oberfläche durch Rotation einer erzeugenden Kurve um eine Rotationsachse gebildet wird.

Rotationskörper berechnen mittels Integration

Aufgabe 1405: spezielle Integrale von trigonometrischen Funktionen. Ein bekannter Rotationskörper ist der Torus.Integration duch Substitution. Integrationsvariable ersetzen.Sichere dir jetzt die perfekte Prüfungsvorbereitung! In diesem Online-Kurs zum Thema Integration durch Substitution bei unbestimmten Integralen wird dir in anschaulichen Lernvideos, leicht verständlichen Lerntexten, interaktiven Übungsaufgaben und druckbaren Abbildungen das umfassende Wissen vermittelt.Sie können ein Doppelintegral in kartesischen Koordinaten in ein Doppelintegral in Polarkoordinaten umrechnen, d. Das Bild zeigt das Werkstück im Querschnitt. Es soll nun im Intervall [0;5] der Rauminhalt von dem Zylinder berechnet werden. Er wird durch die Rotation eines Kreises gebildet. integral; rotationskörper + 0 Daumen. Ergebnis: Das Volumen der Düse beträgt V D =2,69cm 3, die Masse ist M=12,13g.Die Integration durch Substitution – auch Substitutionsregel – ist eine Regel der Mathematik um Funktionen zu integrieren. Die Kurve liegt dabei in einer Ebene, und auch die Achse liegt in ebenderselben. Nun wird die Substituition differenziert. zusammengesetzte Aufgaben zur Statistik. Du erhältst einen Rotationskörper, wenn du eine Fläche (z.x20 − 8×0 + 16 = 0 √ x02/3 = 4 ± 42 − 16 x02/3 = 4 ± 0 x02 = 4 Mit diesen beiden Wert. (00:17) Die wichtigsten Integrationsregeln findest du hier zusammengefasst.Um das Volumen des Glases zu bestimmen, wird das Volumen des inneren Rotationskörpers vom Volumen des äußeren Rotationskörpers subtrahiert.Der Integralrechner berechnet online Stammfunktionen und Integrale beliebiger Funktionen – kostenlos! Mit diesem Online-Rechner kannst du deine Analysis-Hausaufgaben überprüfen.Wie du die Grenzen eines bestimmten Integrals mit substituierst und als unbestimmtes Integral löst, erklären wir dir anschaulich in diesem Kurstext.Bestimmtes Integral – Volumen eines Rotationskörpers. Wenn in einem Integral die Verknüpfung von zwei Funktionen (also irgendeine Art f (g (x)) f (g(x))) steht, kann eine Substitution das Integrieren vereinfachen. Die allgemeine Formel für das Volumen eines Zylinders ist V = πr²·h. Nun folgt ein generell gültiger Schritt. Da eine Volumeneinheit ein Liter . Schritt 1: Nenne die innere Funktion : Schritt 2: Bestimme die Ableitung von , benutze dabei die Differentialschreibweise und löse nach auf: Schritt 3: Ersetze im Integralausdruck . ß ∬ A f ( x, y) d A = ∫ φ = α φ = β ( ∫ r = r innen ( φ) r = r außen ( φ) f ( r, φ) ⋅ r d r) d φ. In dieser Aufgabe soll die Integration durch Substitution durch Übungen trainiert werden. Wir erklären dir Schritt für Schritt, wie du eine Funktion umformst, um sie einfacher zu integrieren.

uneigentliche Integrale

Lösung: Das ist ein uneigentliches Integral erster Art mit zwei kritischen Integralgrenzen. Der Integralrechner von Simplexy kann beliebige Funktionen für dich integrieren und noch viel mehr. Berechnen Sie das Volumen des entstehenden Rotationskörpers. ein Rechteck) um eine Achse im Koordinatensystem herumdrehst.Integrale, die per Substitution gelöst werden können. alte Klausuraufgaben zur Integration durch Substitution. Berechnen Sie das Integral von 0 bis 6 des Rotationskörpers zur Ursprungsgeraden der Funktion f (x . Zuerst substituiert man ² g . Mitsubstituieren der Grenzen des bestimmten Integrals. Den zu substituierenden Term bestimmen. Die Integration erfolgt dabei in zwei Schritten, zuerst kommt die innere Integration über r, danach die äußere . Jetzt weiter lernen! Diese Methode kann immer dann angewandt werden, wenn der Integrand einen Term der Art , oder enthält. Übung zum Integrieren mit linearer Substitution.Aufgabe 1403: Integralberechnung durch Partialbruchzerlegung.Bei der Integration durch Substitution wendet man die folgende Integrationsformel an: b g (b) : f ( g (x) ) ·g’ (x) dx = : f (z) dz .man kann nur Konstante vor das Integral ziehen, keine Terme mit x !. Schaffst du es, Volumen und Oberflächen von Rotationskörpern zu berechnen? Teste dich mit diesen gemischten Aufgaben! Ein rotationssymmetrisches Werkstück soll aus Gusseisen der Dichte 7 {,}2\frac g {cm^3} 7,2cm3g hergestellt werden. das Volumen bei Rotation der Funktion um die y-Achse sei V y.

Integralrechnung

Mathematik-Online-Aufgabensammlung: Integral: Berechnung

Hinweis: Das Integral ist durch Substitution zu lösen! Problem/Ansatz: Ich bekomme das .Integriere und rechne aus: Lösung: Erledigen. Zur Herleitung der Gleichung für M wird der Rotationskörper längs der x-Achse in n Scheiben der Dicke ∆ x zerlegt, jedoch nicht wie bei der Herleitung des Rotationsvolumens in zylindrische Scheiben (vgl. ⇒ Hier erfährst du, wie du mit Integralen das Volumen von Körpern berechnest, welche durch Rotation um die x-Achse .Aufgaben zu Rotationskörpern.

Integrieren durch Substitution

In diesem Abschnitt findet ihr Übungen, Aufgaben, Übungsaufgaben bzw. Berechnen Sie die Volumina der Rotationskörper, die durch Rotation des Schaubildes von f(x) um die x- oder y-Achse im Bereich [a; b] entstehen und beschreiben Sie ihre Form durch je eine der folgenden Bezeichnungen: Zylinder, Kegel, Kegelstumpf, Glocke, Sektkelch ohne Stiel, Kugel, Trompete, Kühlturm (Hyperboloid .) setzen wir für 3 – 7x nun z ein und für dx nun dz durch -7.

Integral Rotationskörper durch Substitution lösen

stochastische Matrizen.Expertenwissen: Rotationskörper.Textaufgaben zur Integralrechnung Lösung. Demnach müssen wir im ersten Schritt uns überlegen was wir am besten substituieren. uneigentliche Integrale.Lerne das Volumen von Rotationskörpern zu berechnen.Die Integration durch Substitution, auch Substitutionsregel genannt, ist eine nützliche Methode in der Integralrechnung, um bestimmte oder unbestimmte Integrale einfacher berechnen zu .

Integration durch Substitution bei bestimmten Integralen

Video: Textaufgaben 5: Rekonstruktion von Beständen

Integration durch trigonometrische Substitution

die Masse der Düse ist gegeben durch M=V D ·4,5g/cm 3 =12,13g.

Stammfunktionsrechner

Gefragt 25 Jun 2023 von Ratloser Student. a g (a) substituere (lat.

Bestimmtes Integral

Integration durch Substitution • einfach erklärt

Die Integration durch Substitution wird immer dann angewandt, wenn eine Funktion mit einer anderen verkettet ist. Substitution vorbereiten. Dies wird in unserem Rotationskörper Rechner numerisch . Gleichung aus Schritt 1 nach auflösen.

Integration durch Substitution

Das Schaubild K rotiert im Intervall [0;4] um die Gerade mit der Gleichung y=4/3. In diesem Kapitel wirst du lernen wie man ein Integral mit der Substitutionsregel lösen kann.Kostenlos Rechner für Volumen für rotierende Körper – Finde das Volumen für Rotationskörper Schritt für SchrittIntegration durch Substitution Du verwendest die Substitutionsregel ähnlich wie beim Ableiten die Kettenregel , also bei verketteten Funktionen. Übung zum Erstellen von Textaufgaben zur Integralrechnung.

Aufgaben zu Rotationskörpern

Substitutionsregel. Wir wollen diese Aufgabe durch Integration durch Substitution lösen.Integrationsregeln Übersicht.Die Substitutionsmethode der Integration oder der Integrationsmethode durch Substitution ist eine clevere und intuitive Technik, die zum Lösen von Integralen verwendet wird.) zunächst eine Substitution durch, leiten ab und stellen nach dx um. Aufgabe mit Lösung.Integration durch Substitution.Aufgabe 2: Rotationsvolumina. Integralrechner . ∫ 0 2 2 x e x 2 d x. Das Volumen von einem . Dies ist eine interaktive Aufgabe zu: Integrieren durch Substitution mit praktischen Tipps zum Lösen und einer Zusammenfassung der .Kostenlos Stammfunktionsrechner – löse Integrale inklusive aller Schritte. Rechnet diese Aufgaben zunächst selbst durch und . In diesem Falle besteht auch der Körper aus mehreren sehr dünnen (h->0 ist die Dicke) Zylindern. Aber zum Üben solltet ihr diese versuchen ohne Spicken zu lösen und erst im Anschluss die . Berechne ganz simple die Stammfunktion und die Flächen unter einem Graphen. Es bietet sich an. Nachdem wir trigonometrische Substitution angewendet haben, erhalten wir ein Integral, welches einfacher zu integrieren ist als vorher. Dann ist das Volumen des Körpers, der durch Rotation der Funktion um die x-Achse entsteht V x, bzw.Die Substitution ist das Gegenstück zur Kettenregel beim Ableiten.

Integralrechnung einfach erklärt • Integral berechnen

Integration by Substitution Part 1 - YouTube

Rotationskörper um Y-Achse. Hast du eine innere Funktion und eine .

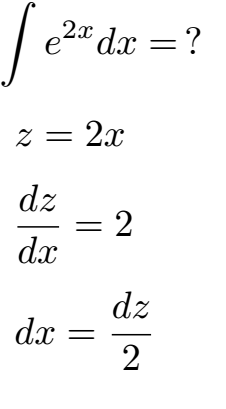
Integration Substitution Beispiel

Diese Aufgaben sind bereits als Beispiele vorgerechnet worden.Bei bestimmten Integral en ist eine Auflösung durch Substitution auf zwei Arten möglich. Gib einfach das Integral ein, um dessen Lösung, Teilschritte und den Graphen zu sehen. [ ∫ u · v ‚ = u · v – ∫ u‘ · v mit u = v ‚ = sin(x) ] Du kannst auch die Reduktionsformel anwenden ( aber dann kannst du auch gleich die Stammfunktion von sin 2 (x) in der gleichen Formelsammlung ablesen 🙂 ):Das Gewicht bzw.Voraussetzungen. Die Vorgehensweise sieht dabei aus wie im ersten Beispiel: Wir führen in Schritt 1. Im Idealfall ist der Integrand sogar schon eine verkettete Funktion multipliziert mit der Ableitung der inneren Funktion, also f (g (x))\cdot g‘ (x) f (g(x))⋅ g′(x .Beispiel 2: Im zweiten Beispiel zur Integration durch Substitution geht es darum eine Sinus-Funktion zu integrieren. Im letzten Schritt wird nach aufgelöst.Hier erfährst du, wie du Integration durch Substitution anwenden kannst. Damit kann das .ten Faktor ergibt sich sofort:x01 = 0Zur Bestimmung der weiteren Nullstellen muss nur no. er zweite Faktor untersucht werden. Auch Kegel und Zylinder sind . Das Volumen aller Zylinder werden aufsummiert und als ein Integral aufgestellt.Die Mantelfläche M eines Rotationskörpers, der durch Rotation einer Randfunktion f um die x-Achse im x-Intervall [a, b] entsteht, soll bestimmt werden. Textaufgaben Rekonstruktion von Beständen Lösung. Hier kannst du mit partieller Integration arbeiten (2-mal) oder mit Substitution.Dies ist eine interaktive Aufgabe zu: Integrieren durch Substitution mit praktischen Tipps zum Lösen und einer Zusammenfassung der nötigen Theorie.