Integrationskonstante Formel – Integralrechnung
Di: Jacob
Gelingt dies nicht sollte u(x) und v'(x) vertauscht werden.Dabei ist $\int$ das Integrationszeichen und $f(x)$ der Integrand.
Variation der Konstanten: Erklärung und Beispiel · [mit Video]
Anschließend zeigen wir anhand einiger Beispiele, wie du damit Integrationsaufgaben in der Praxis lösen kannst. Die freie Lernplattform. Umfassende Unterstützung: Maths2mind begleitet Schüler bis zum .Konstante (Mathe): Variable Lineare Funktion Ableiten Konstantenregel Beispiele StudySmarter Original Sie ist aus der Aufgabe entstanden, . Weitere Beispiele und Erklärungen findet ihr unter: Faktorregel Integration; Integrationsregel Summenregel: Summen und Differenzen dürfen gliedweise integriert werden. Dieses c ist die Integrationskonstante.Es folgt zunächst die allgemeine Formel, im Anschluss gibt es einige Beispiele.Verständliche Erklärung der Integralrechnung – inklusive vielen Beispielen, leicht verständlichen Definitionen, kostenlosen Lernvideos und Tipps. Bredt’sche Formel so darstellen, dass die maximale Spannung als Quotient von Torsionsmoment durch .
Der EBA- Stresstest 2025 im Überblick
Geschätzte Lesezeit: 7 min
Integrationskonstante
Vielen Dank! Springe zum Inhalt oder Footer.WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du diesen Dialog öffnest.Integrierverstärker – Tiefpass mit OPV.Bei der Integration durch Substitution muss man einige Punkte beachten.Quader Eigenschaften, Formeln und Beispiele; Bruch in Dezimalzahl umwandeln Beispiele; Textaufgaben Klasse 5 (Mathematik) Umfang Rechteck Formel und Beispiele; Rechnen mit negativen Zahlen; Zahlengerade Erklärung und Beispiele; Teilerfremd berechnen Beispiele; ggT größter gemeinsamer Teiler Erklärung Jetzt folgt ein Beispiel, um die Variation der Konstanten zu üben: Die homogene Lösung von.Die Integrationskonstante wird in allen Fällen mit c = 0 angenommen.
Partielle Integration / Produktintegration
Die Variable C ist die Integrationskonstante.TM2 – Konstante und örtliche Dehnung im Stab [Formeln, Beispiele, Berechnung] Zu unseren Angeboten.Er wird manchmal der Einfachheit halber weggelassen (sollte aber dann zumindest dazugedacht werden). Fächer Über Uns Spenden; Mitmachen Anmelden; Mathematik Funktionen Stammfunktion, Integral und Flächenberechnung Integrale .

Stefan Boltzmann Gesetz · Herleitung & Beispiel · [mit Video]
Die Integralrechnung ist ein Zweig der Infinitesimalrechnung und bildet mit der Differentialrechnung die mathematische Analysis. Kurz und kompakt haben wir für dich . ist gleich ist die e-Funktion mal einer Konstanten C. F (x)=3x+4 und F (x)=3x+7 sind zum Beispiel beide .Wie wird die Differentialgleichung der Biegelinie hergeleitet? Das erfährst du ganz einfach und anschaulich hier.Das Stefan-Boltzmann-Gesetz ist nach dem Physiker Josef Stefan (1835-1893) und dem Physiker Ludwig Boltzmann (1844-1906) benannt. Zeit für ein paar Beispiele um die partielle Integration zu zeigen. Das Zeit-Weg-Gesetz für gleichförmige Bewegungen. • Zweimalige Ableitung der Biegelinie führt demzufolge . • Lösung: Wir müssen den Momentenverlaufzweimal ableiten und erhalten so die Streckenlast q. • Temperaturdifferenz (Regeldifferenz . Die Eigenschaften einer OPV-Schaltung werden von den externen Bauteilen bestimmt.Man schreibt also das Integralzeichen ∫ mit der unteren Integrationsgrenze a darunter und der oberen Integrationsgrenze b darüber, gefolgt von der betrachteten Funktion sowie .• Diese mathematische Formel ist die Grundlage der Elotech PID-Reglers –P = Proportionalanteil = –I = Integralanteil = –D = Differentialanteil = –Regelstrecke • z. Wissenspfade: Zu jeder Lerneinheit werden gut strukturiert empfohlenes Vorwissen, verbreiterndes und vertiefendes Wissen angezeigt. Dieses Gesetz stellt einen Zusammenhang zwischen der Strahlungsleistung, der Fläche des schwarzen Körpers und der Temperatur auf.Der Zusatz + c soll anzeigen, dass die Stammfunktion nur bis auf eine (beliebige) Konstante (die so genannte Integrationskonstante) eindeutig ist.Hauptsatz der Differential- und Integralrechnung.Das Integral der Kotangensfunktion ist der positive Logarithmus vom Betrag der Sinusfunktion plus die Integrationskonstante. Beispiel: f (x) = 3 x² , das heisst, F (x) = x³ + c .Der EBA – Stresstest 2025 im Überblick.Um ein unbestimmtes Integral zu berechnen, musst du die Stammfunktionen F (x) von finden.Konstantenregel oder Faktorregel.Bestimmtes Integral einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen! Dafür brauchst du zuerst die sogenannte Stammfunktion.Unser Tutor Markus erklärt in diesem Video die Integrationskonstante. Dabei ersetzen wir . Integrale der Funktion f(x) = x 2.deIntegralrechnung Übungen und Aufgaben mit Lösungen | .Integrationskonstante) F(x) = 1/3 x 3 + C und das sind dann Stammfunktionen bzw.Die Integralrechnung hilft dir, Flächeninhalte zwischen der x-Achse und einer Funktion auszurechnen. Inhaltsverzeichnis: Dehnungen im Stab beziehen sich auf die Verlängerung des Stabes entlang seiner Längsrichtung, wenn er einer Zugkraft ausgesetzt ist.
Die Integrationskonstante
Ist nun der Weg gesucht, muss man die Geschwindigkeit nach der Zeit t integrieren. Juli 2024 veröffentlicht. Das bestimmte Integral lässt sich mit der . Wie bei der Torsion von Kreisprofilen lässt sich auch die 1.
Kotangens integrieren
besagt mit der Formel von Newton und Leibnitz wie das bestimmte Integral aus dem unbestimmten Integral hervorgeht. Wärmeentnahme (Störgröße z) • Ist-Temperaturwert (Istwert /Regelgröße x) • Wunschtemperatur (Sollwert /Führungsgröße w). Durch sie wird klar, dass ein Wert durch das Ableitung eventuell verloren gegangen ist. Die Proportionalitätskonstante heißt Stefan Boltzmann Konstante . Der Vorgang, eine Stammfunktion zu einer gegebenen Funktion zu finden, heißt integrieren.

Integrationsregeln » einfach erklärt mit Beispielen
Bewegt sich ein Objekt für die Zeit mit der Geschwindigkeit , so beträgt . Der Hauptsatz der Differential- und Integralrechnung auch der Fundamentalsatz der Analysis liefert.Geschätzte Lesezeit: 50 Sekunden
Integralrechnung einfach erklärt • Integral berechnen
Sie schließt die Lücke zwischen Integral- und Differentialrechnung.C steht für die Integrationskonstante.Man verdeutlicht dies, indem man hinter eine allgemeine Stammfunktion den Term +C +C ergänzt, wobei die sogenannte Integrationskonstante C für eine beliebige Zahl aus . Das Integral u'(x) · v(x) dx muss elementar lösbar sein.Die Formel sieht recht willkürlich aus, ist aber von beachtlicher Effizienz.

Aufleiten • Aufleitungsregeln mit Beispielen · [mit Video]
Flächeninhalt zwischen Graph und x-Achse.Einen konstanten Faktor im Integranden kann man vor das Integrationszeichen ziehen, wodurch sich die eigentliche Integration vereinfacht. Die allgemeine Formel sieht leider sehr unschön . Dazu gibt es verschiedene Integrationsregeln , die wir dir ausführlich in einem separaten Video . Dazu ziehen wir die 3 vor das Zeichen für die Integration und belassen es bei x dx dahinter. Hier findest du folgende Inhalte.Das bestimmte Integral besitzt im Gegensatz zum unbestimmten Integral Grenzen, die sogenannten Integrationsgrenzen und . Somit gibt es auch unendlich viele Möglichkeiten, wie die Stammfunktion aussehen kann. Beim sogenannten unbestimmten Integral (Integral ohne Grenzen) kommt immer eine Stammfunktion der . Sie ist dennoch sehr nützlich, denn sie hilft uns, das Integral so zu vereinfachen, dass wir leichter integrieren können.
Integrationskonstante
∫f(x)dx=∫f(φ(z))⋅φ′(z)dz. \(\eqalign{ & f\left( x \right) = \cot x \cr & .


Da Konstanten beim Ableiten einfach wegfallen, kann C jede beliebige Zahl sein.Partielle Integration Formel: Tipps zur Produktintegration: Das Produkt muss so in u(x) und v'(x) zerlegt werden, dass für v'(x) eine einfache Integration möglich ist. die Geschwindigkeit v(t) bekannt. Dazu gleich eine kleine Warnung: Ihr müsst am Anfang u und v‘ festlegen. Hier zwei Beispiele für unbestimmte Integrale: .Auf der Seite Formeln umstellen wird Schritt für Schritt anhand vieler Beispiele erklärt, wie man physikalische Gleichungen umstellt.
![Bestimmtes und unbestimmtes Integral • einfach berechnen! · [mit Video]](https://d3f6gjnauy613m.cloudfront.net/system/production/videos/001/860/56dae9a240bf22eeaa1096fc018064e96cbe11a5/Thumbnail_Bestimmtes_und_unbestimmtes_Integral.png?1670579949)
Konstantenregel beim Integrieren
Im Weiteren wird auf die Herleitung der Formeln verzichtet.Soll mit dem Integral die Fläche zwischen dem Funktionsgraphen und der -Achse in einem bestimmten Intervall berechnet werden, dann setzen wir die Intervallgrenzen für und ein. Tauscht in diesem Fall u und v‘ einmal .I dette afsnit ser vi på stamfunktioner, det ubestemte integral, regnereglerne for integraler, det bestemte integral samt arealet af en funktion og mellem to funktioner. Die 3 davor bleibt stehen und wird mit dem Rest .Bredt’sche Formel bestätigt die Folgerung aus dem hydrodynamischen Vergleich, dass die Torsionsspannungen an der Stelle der geringsten Wandstärke maximal werden. das Integral der Beschleunigung.Das Integral der Kotangensfunktion ist der positive Logarithmus vom Betrag der Sinusfunktion plus der Integrationskonstante.Integralrechnung. Der Ansatz für die Lösung mit Variation der Konstanten lautet:
Bestimmtes Integral berechnen
Weg, Geschwindigkeit, Beschleunigung & Ruck
Wir stellen einfache Integrale auf un. Dieses c [mm] .
Torsion von dünnwandigen, geschlossenen Profile
Wenn man die Funktion f(x) integriert, erhält man die .comEmpfohlen auf der Grundlage der beliebten • Feedback
Integralrechnung
In diesem Zusammenhäng erklären wir zunächst die Integrationsformel und beweisen deren Gültigkeit.Das bestimmte Integral einer stetigen Funktion f (x) kann berechnet werden, indem man die Differenz der oberen – und der unteren Grenze der Stammfunktion F (x) bildet. Einen konstanten Faktor im Integrand kann man vor das Integrationszeichen ziehen, wodurch sich die eigentliche Integration vereinfacht. Das Integral ist ein wichtiges Konzept in der Mathematik.
Integrieren: Stammfunktionen, Beispiele & Rechenregeln
Damit kann man dann rechnen, beispielsweise die . Wählt ihr diese falsch herum aus, könnt ihr die Aufgabe unter Umständen nicht mehr lösen.
Bestimmtes Integral ⇒ einfache & ausführliche Erklärung
Stammfunktionen und Integrationsregeln
Das Integral der konstanten Funktion f (x) = k wird wie folgt berechnet: $$y=f (x)=k F (x)=∫k\, dx=k·x+C$$ Das dx am Ende des Integrals besagt, dass die . Es werden die wichtigen Formeln zur Berechnung des Schubflusses und der Schubspannung bei dünnwandingen geschlossenen Profilen aufgeführt: Die Schubfluss ist gegeben durch [auf die Herleitung wird verzichtet]: Die Europäische Bankenaufsichtsbehörde (EBA) hat den Entwurf für die Regeln des EBA-Stresstests 2025 am 5.Integralrechnung einfach erklärt und leicht nachvollziehbar! – .Konstante integrieren verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Steht im Integrand nur eine Konstante, so ist deren Integral die Konstante mal derjenigen Variablen, nach der integriert wird.Die allgemeine Formel lautet wie folgt: Es folgt ein einfaches Beispiel mit der Faktorregel (und zusätzlich der Potenzregel). der Multiplikationsfaktor bleibt . den Zusammenhang zwischen der Differential- und der Integralrechnung; besagt mit der Formel von Newton und Leibnitz wie das bestimmte Integral aus dem unbestimmten Integral hervorgeht.• Wir betrachten nun einen Lastverlauf, Formel für Biegelinie nicht mehr so einfach verwendbar! • Wir brauchen nämlich den Momentenverlauf, können ihn aber nicht so schnell bestimmen. Die Variable $x$ heißt Integrationsvariable und $C$ ist die Integrationskonstante.Einfaches Beispiele zur Formel: Integriert werden soll die einfache Funktion f(x) = 3x nach der Variablen x (daher das dx dahinter).Wenn du eine Funktion f (x) integrierst, erhältst du als Stammfunktion F (x) + c .Integralrechnung einfach erklärtIn diesem Mathe Lernvideo erkläre ich (Susanne) die Einführung in die Integralrechnung.Du brauchst die Integrationskonstante, weil es für eine Integrationsfunktion f (x) unendlich viele Stammfunktionen F (x) gibt. Wenn du zum Beispiel an beiden Enden eines Stabes ziehst, wird er sich in Richtung . Möchte man die Beschleunigung wissen, ist die Geschwindigkeit abzuleiten (= differenzieren). Durch die Potenzregel der Integration können wir das x integrieren zu x 2: 2. Berühmt ist Kepler .Die Geschwindigkeit v(t) ist also die Ableitung des Weges bzw.Kotangens integrieren verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Das Integral der Kotangensfunktion ist der positive Logarithmus vom Betrag der Sinusfunktion plus der IntegrationskonstanteWichtige Formeln. Gelegentlich wird sie übrigens auch als Kepler’sche Fassregel bezeichnet, weil es Johannes Kepler war, von dem sie in ihrer einfachsten Form stammt – angeblich hatte er sie entwickelt, um das Volumen von Weinfässern zu bestimmen.

Es ist neben der Differenzierung eines von zwei Hauptoperationen in der Infinitesimalrechung. Anzeige: Anzeigen: . Sind zusätzlich zu ohmschen Widerständen auch kapazitive und induktive Blindwiderstände wirksam, dann wird das Verhalten der Schaltung frequenzabhängig. Dies ist eine der wichtigsten Fähigkeiten, die Du zum Lösen zahlreicher Physikaufgaben benötigst.
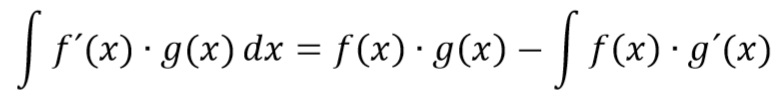
Die Integrationskonstante $C$ steht für eine beliebige reelle Zahl ($C\in\mathbb{R}$) und ist bei unbestimmten Integralen von Bedeutung. – Perfekt lernen im Online-Kurs Baustatik 1Variation der Konstanten: Beispiel. Das gilt besonders für komplexe Formeln und anschauliche Illustrationen. Sehen wir uns einige Beispiele zur Produktintegration an.
- P2 Abschminkpads, 2 Stück, 3Er Multipack
- Kind Will Sich Nicht Die Haare Schneiden Lassen
- [Solved] Run Vlc Portable On Ubuntu 10
- Truppenbesuch Beim Einsatzführungsbereich 2 In Erndtebrück
- 283 Propiedades E Inmuebles En San Cristóbal De Las Casas
- Hisense 100U7Kq Mini Led Tv (Flat, 100 Zoll / 253 Cm, Uhd 4K
- All-In-One Desktop Touch Screen
- Kabel Bw Störung Heidelberg: Aktuelle Störungen Heute!
- Mobile First , So funktioniert der Mobile-First Index
- Gyógyszer Egyedi Méltányossági Kérelem
- Gewa Multimedia Online Shop – test 07/2024