NNKJW

XSB

Konstruiere Die Folgenden Dreiecke

Di: Jacob

Gib jeweils an, welcher Kongruenzsatz vorliegt und konstruiere dieses Dreieck. Das andere Dreieck wäre dann auch keine Spiegelung des richtigen Dreiecks mehr (nur wenn der Winkel zufällig 90° betrüge, wäre das der Fall.Dreiecke konstruieren leicht und verständlich erklärt inkl. Konstruiere die folgenden Dreiecke ABC, wenn es möglich ist.Daher gilt folgende Formel für den Flächeninhalt. a) a = 3,5 cm; b = 4 cm; α = 60° b) a = 2,8 cm; c = 4,8 cm; γ = 110° c) b = 4 cm; c = 5 cm; β = 70° d) b = 4,2 cm; c = 6,2 cm; β = 40° Beim . Wird das Dreieck nun im Schwerpunkt – dem Schnittpunkt der Schwerelinien – gehalten, ziehen die Flächen auf den beiden Seiten der Schwerelinien jeweils mit gleicher Kraft nach unten.Konstruktionsbeispiele. Berechne den Flächeninhalt des Dreiecks. Aber auch ein Verbalisieren der Arbeitsschritte ist wichtig und kann beim Besprechen geübt werden.atEmpfohlen auf der Grundlage der beliebten • Feedback

Dreieck konstruieren / zeichnen

Hier findest du Aufgaben zur Konstruierbarkeit von Dreiecken.atmathe-lexikon.Konstruiere ein Dreieck ABC nach den folgenden Angaben und beschreibe die Konstruktion a) c = 6 cm, = 90° und h c = 2 cm b) a = 5 cm, = 90° und h a = 1,5 cm c) b = 7,8 cm, = 90° und h b = 3,2 cm Aufgabe 13 Konstruiere die Tangenten durch den Punkt P am Kreis k mit Mittelpunkt M mit Hilfe des Thaleskreises: Aufgabe 14 Dreieck 6 ist Dreieck 5 gespiegelt.Überbestimmte Dreiecke Konstruiere mindestens zwei der folgenden Dreiecke. Konstruiere ein Dreieck mit den Seitenlängen a=3\;cm;\;\;\;b=\;4\;cm;\;\;c=\;5\;cm\; a = 3 cm; b = 4 cm; c = 5 cm.

Dreiecke konstruieren - Kongruenzsatz SWS - YouTube

Abbildung 9: Ankreise Dreieck konstruieren. Nie wieder schlechte Noten!

Dreieck • Dreieck konstruieren, Beschriftung Dreieck

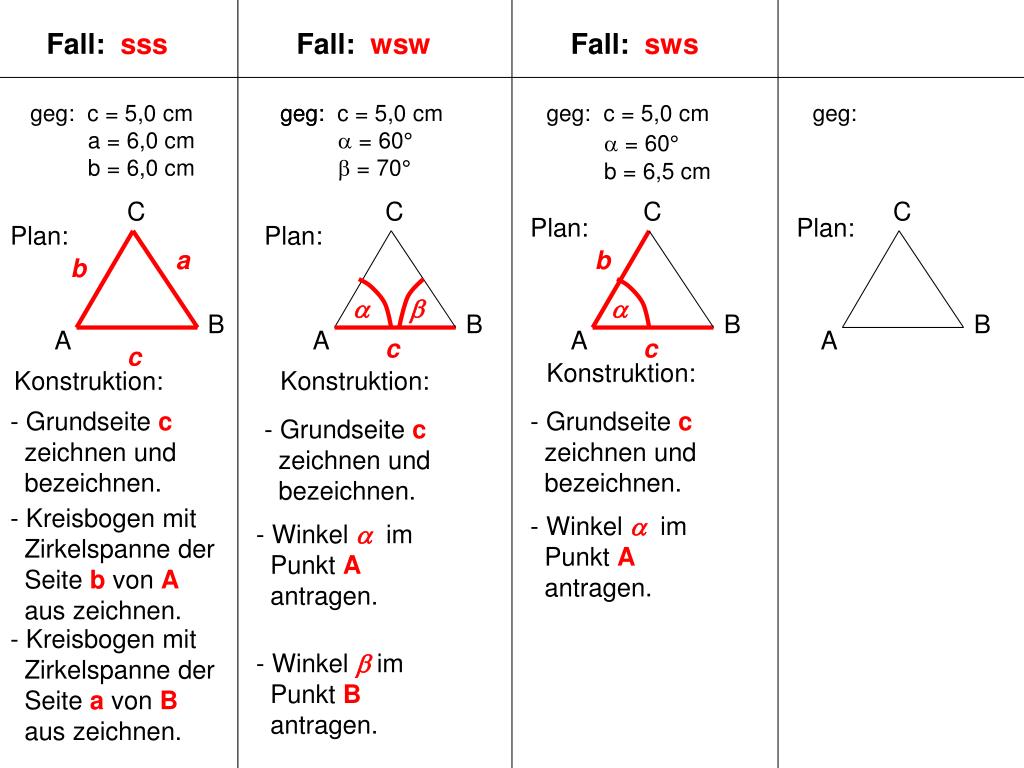
PPT - Dreiecke konstruieren PowerPoint Presentation, free download - ID ...

: Abbildung 10: Ankreise Dreieck konstruieren.Die den Punkten jeweils gegenüber liegenden Strecken werden kurz als , und , die Innenwinkel als , und bezeichnet. Folgende Konstruktionssätze gibt es: a. Aufgabe 1: Verändere die untere Figur mit Hilfe der orangen Gleiter so, dass die Seite a 10 cm, die Seite b 11 .

A8 Ich konstruiere Dreiecke nach SSW auf Grund einer vorliegenden ...

Um den Schwerpunkt eines Dreiecks konstruieren zu können, solltest Du wissen, wie Du die Seitenhalbierenden konstruierst, denn: Der Schwerpunkt eines Dreiecks ist der Schnittpunkt der drei Seitenhalbierenden.

Konstruiere die folgenden Dreiecke

Zeichne die Strecke c der Länge 8 cm mit den Endpunkten A und B. Aufgabe 4: Konstruiere das rechtwinklige Dreieck ABC mit den Katheten b=6cm und c=8cm.

Dreiecke konstruieren (SSS)

deklassenarbeiten. Aufgabe Zeichne jeweils die Symmetrieachsen ein.

Vierecke konstruieren Übungen

Man unterteilt die Dreieckskonstruktionen in Konstruktionen aus Seiten und Winkeln (Grundkonstruktionen) und in Konstruktionen, bei denen auch weitere Bestimmungsstücke wie Höhen, Winkelhalbierende gegeben sind. Die Nebenwinkel , und der Innenwinkel .

Konstruieren Sie beide Dreiecke und bestimmen Sie die

) Das heißt, es gibt wirklich nur genau ein Dreieck, das bei der Konstruktion mit SsW entsteht.Konstruiere Dreiecke aus den gegeben Stücken. Abbildung 21: Dreieck konstruieren.Entdecke die verschiedenen Arten von Dreiecken, lerne wie du ihre Seiten und Winkel bestimmst und erfahre, wie du den Umfang und die Fläche eines Dreiecks berechnest. Trage den Winkel a an A an. Re-konstruiere die folgenden Dreiecke.Konstruiere ein Dreieck mit folgenden gegebenen Werten und benutze dafür den passenden Kongruenzsatz.

Schwerpunkt eines Dreiecks: konstruieren

Aufgaben und Lösungen zum Video auf www.Aufgabe 14: Konstruiere die folgenden Dreiecke mit Inkreis und miss die fehlenden Innenwinkel und Seiten.Geometrie – Winkel, Konstruktion von Dreiecken Dauer ca. Klicke auf eine der .5cm : LÖSUNG: TOP: Aufgabe 26 : Von einem gleichschenkligen Dreieck sind die Achse und drei Punkte gegeben. Abbildung 22: .Es muss gelten, dass die Summe der beiden kürzeren Seiten größer als die längste Seite sein muss. Beschrifte sie komplett und markiere gegebene Stücke rot.Bestimmungsstücke, um ein Dreieck konstruieren zu können.

Den Kongruenzsatz WSW nutzen

c=5\;cm\;;\;\alpha=50^\circ\;;\;\beta=60^\circ c = 5 cm; . Entscheide, ob man aus folgenden Angaben eindeutig Dreiecke konstruieren kann.

Dreiecke konstruieren, Kongruenzsätze, Dreiecksungleichung - © www ...

Um den Flächeninhalt des Dreiecks zu berechnen, müssen wir die Höhe und die Basis des Dreiecks kennen.deDreiecke – Konstruieren mit GeoGebra – GeoGebrageogebra. Trage den Winkel α an A an.

Dreieckskonstruktionen

Aufgabe 5: Zeichne drei verschieden große rechtwinklige Dreiecke mit der Übungen und Klassenarbeiten. Der Schnittpunkt des Kreisbogens mit dem freien Schenkel des Winkels a ist die Ecke C des Dreiecks.Die Konstruktion von Dreiecken ist anhand sogenannter Bestimmungsstücke mithilfe von Zirkel und Lineal durchführbar.Konstruieren Sie ein Dreieck aus c=10cm alpha=60 grad und beta=43 grad und ermitteln Sie aus Ihrer Zeichnung die Radien von In-und Umkreis. Die Formel ist aufgrund des rechten Winkels zwischen den zwei bekannten Seiten sehr ähnlich der . Denn dann sind alle Dreiecke, die du .Zeichne die Strecke c der Länge 8 cm mit den Endpunkten A und B. Dreiecke bestehen aus den Verbindungsstrecken zwischen drei Punkten , und , die nicht auf einer gemeinsamen Geraden liegen. Zuerst zeichnest Du die Grundseite c = 4cm. Ich habe folgendes gezeichnet, muss ich den in- und umkreis noch berechnen, wenn ja wie ? Aufgabe 2: Es gibt zwei Dreiecke, die die Vorgabe b=7cm alpha=50 grad und a=6cm .Konstruiere die Menge aller Punkte, die näher bei M als bei A liegen, aber weniger als 35mm von A entfernt sind.Vierecke konstruieren Übungen jetzt online lernen Mit SCHÜLERHILFE schlechte Noten verbessern. ge in diese die gegebenen Größ.Alternativ zum Arbeitsbogen ‚konstruiere die folgenden Dreiecke’ kann der Arbeitsbogen ‚Überbestimmte Dreiecke‘ eingesetzt werden.Kongruenzsätze für Dreiecke – Übungsköniguebungskoenig. Aufgabe Konstruiere die folgenden Dreiecke aus den angegebenen Größen sauber mit Zirkel und Lineal.Ein Dreieck mit drei vorgegebenen Seiten konstruieren (SSS) Neu. Zirkel und Lineal zu konstruieren. Das Dreieck ist nicht eindeutig konstruierbar.Schwerpunkt eines Dreiecks konstruieren.Suche zu jedem Kongruenzsatz aus den Aufgaben 1) bis 13) eine heraus, die dazu passt.

Dreiecke konstruieren

Im allgemeinen Dreieck gelten die folgenden Bezeichnungen: A, B, C: Eckpunkte des Dreiecks a, b, c: Dreiecksseiten (AB = c; BC = a, AC = b) α, β, γ: Winkel im Dreieck (α = BAC, β = ABC, γ = BCA) 2. Höhe auf die Seite i . Ist es eindeutig konstruierbar? Beschreibe, wie du vorgehst.Um ein bestimmtes Dreieck konstruieren zu können, müssen wir bestimmte Angaben, Seiten ( s) und Winkel ( w ), kennen.Entscheide, ob man aus folgenden Angaben eindeutig Dreiecke konstruieren kann.Die Dreiecke 5 und 6 sind ebenfalls zueinander kongruent, auch wenn hier die rechts und links anliegenden Winkel vertauscht sind.Dreiecke konstruieren mit sss sws wsw ssw – einfach erklärt.Zum Konstruieren eines Dreiecks mit Zirkel und Geodreieck sind folgende Grundkonstruktionen zu unterscheiden: drei Seiten sind gegeben (SSS) zwei Seiten und .Konstruieren Sie die folgenden gleichseitigen Dreiecke: a) h=5cm: b) Umkreisradius r=3cm: c) Inkreisradius ρ=1.Konstruiere die folgenden Dreiecke aus den angegebenen Größen sauber mit Zirkel und Lineal. Fertige zuvor jeweils eine Planfigur an und be-

Dreieck: Eigenschaften, Arten, Berechnen & Winkel

a) a = 7 cm b = 5 cm γ = 120o b) a = 5 cm b = 4 cm c = 8 cm c) α = 60o β = 25o c = 6 cm 2.

Aufgaben zur Konstruierbarkeit von Dreiecken

Dreiecke werden nach zwei Kriterien eingeteilt: Länge der Seiten: ungleichseitig, gleichschenkelig (2 gleich lange Seiten), gleichseitig. Seite-Seite-Seite-Satz (SSS) Ein Dreieck ist eindeutig . Fertige eine Planskizze an, beschreibe die Konstruktion und miss die fehlenden Größen: c=5 cm; β=109°; h c =5,6 cm Lösung: a=4 cm; c=4,5 cm; h c =3,5 cm Lösung: a=3,8 cm; α=50°; h c =3,6 cm Lösung: a=4,6 cm; c=4,4 cm; h b =4,2 cm Lösung: c=7,8 cm; γ=47°; h b =7,3 cm Lösung: zurück zur . Konstruiere das Dreieck mit Geogebra. Seitensymmetrale (Mittelsenkrechte) der Seite i Das Dreieck ist eindeutig konstruierbar. Alle drei Seitenhalbierenden schneiden sich in einem Punkt im .

Dreieckskonstruktionen und Kongruenzsätze

Zeichne eine Planfigur.Im Folgenden soll ein reguläres Dreieck (= gleichseitiges Dreieck) mit der Seitenlänge c c c konstruiert werden. Aufgaben: ieck .Allgemeine Eigenschaften¶. 1) Konstruiere das Dreieck ABC, fertige zunächst eine Planfigur an. Dabei geht die Basis durch R, ein Schenkel geht durch P und der andere durch Q. Danach zeichnest Du eine beliebig lange Linie im Winkel \( \beta \) = 50° zu der Grundseite c. Ein Dreieck wird eindeutig festgelegt durch die Angabe (vergleiche mit den Kongruenzsätzen) aller drei Seitenlängen; einer Seitenlänge und zweier Winkel; zweier Seitenlängen sowie dem Zwischenwinkel; zweier Seitenlängen und dem Winkel, der der größeren Seite . Gib an, welchen Kongruenzsatz du dabei verwendest. Und wenn ja, konstruiere das Dreieck.

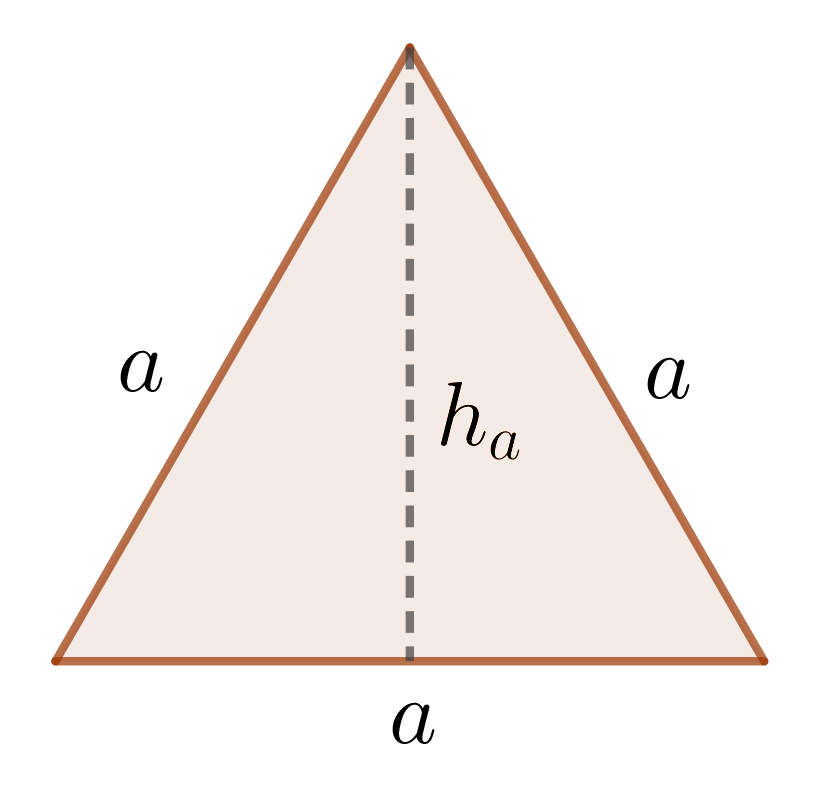
Dreiecke konstruieren in Klasse 8 Arbeitsblätter

Mit dem Schieberegler kann man sich die Konstruktion Schritt für Schritt anzeigen lassen. Seiten des Dreiecks . Wenn die drei Seitenlängen eines Dreiecks gegeben sind, so lässt sich dieses Dreieck eindeutig konstruieren (SSS). Zeichne einen Kreisbogen mit dem Radius 5 cm um A. Wie groß ist die Summe der Innenwinkel in einem 5 – Eck? Gibt es ein Vieleck, dessen Innenwinkelsumme 900 Grad beträgt? Wenn ja, um welches n-Eck handelt . a = 2cm \( \beta \) = 50° Lösung.Mit den folgenden Konstruktionsaufgaben kannst du dein Wissen hierzu testen. Zeichne eine Gerade und wähle darauf den Punkt A des Dreiecks aus.Erläuterungen zum Arbeitsbogen ‚Konstruiere die folgenden Dreiecke‘ Voraussetzungen : Die Schülerinnen und Schüler kennen die Bezeichnungen der Kongruenzsätze SSS, .Die fehlende Seitenlänge beträgt also etwa 7,07 cm. Dafür gibt es mehrere Möglichkeiten. Wir können dann die .Konstruieren sie einen Dreieck aus (unten stehen die werte) und ermitteln sie aus Ihren Zeichnungen die Radien von In- und Umkreis! a) c= 10 cm, Alpha = 60 grad, beta = 43 grad b) Es gibt zwei Dreiecke, die die Vorgabe b= . Aufgaben 1 Konstruiere die folgenden Dreiecke.In diesem Kurs lernst du ein Dreieck mit z.

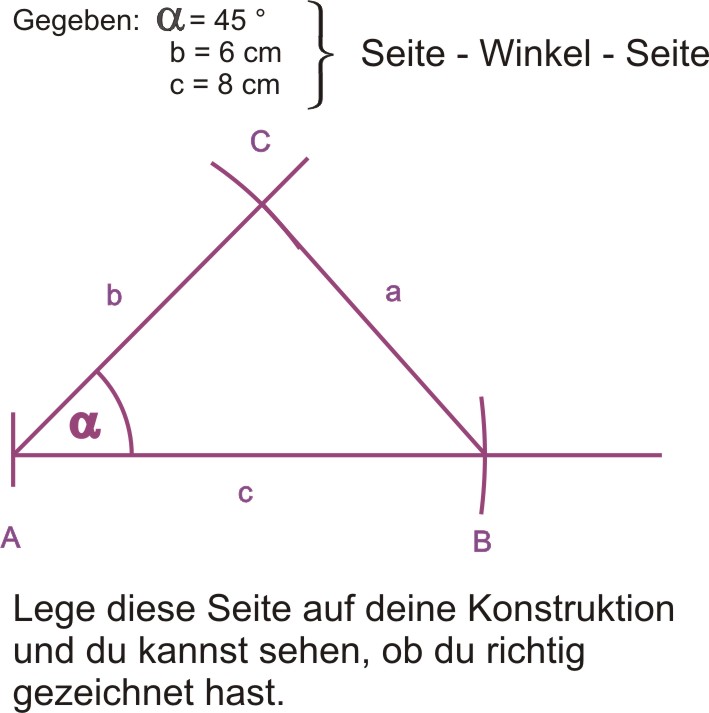
Dreiecke konstruieren - A (SWS)

Dabei werden verschiedene Beispiele vorgezeichnet und erklärt.deArbeitsblätter zum Thema Dreiecke – mathe-lexikon. Du musst drei Größen des Dreiecks kennen und .

Kongruenzsätze: Dreiecke konstruieren

Es werden folgende Bezeichnungsweisen gewählt: a, b, c . SchrittJetzt bestimmst Du den Schnittpunkt M der Winkelhalbierenden mit den Außenwinkelhalbierenden.orgEmpfohlen auf der Grundlage der beliebten • Feedback

Dreieck • Dreieck konstruieren, Beschriftung Dreieck

Miss die Weiten der Innenwinkel und die Längen der . c = 5 c m ; α = 5 0 ∘ ; β = 6 0 ∘ c=5\;cm\;;\;\alpha=50^\circ\;;\;\beta=60^\circ c = 5 c m; α = 5 0 ∘; β = 6 0 ∘.Konstruiere ein Dreieck ABC mit b = 5 cm; c = 8 cm und α = 65°.Du kannst ein Dreieck konstruieren, wenn die gegebenen Stücke einen der Kongruenzsätze erfüllen und die Seitenlängen die Dreiecksungleichungen erfüllen.Aufgabe: Folgende Maße sind von einem Dreieck gegeben: a = 4 cm, b = 5 cm, c = 6 cm 1. Dort sind bei jedem Dreieck mehrere .Abbildung 3: Eine Schwerelinie eines Geodreiecks. SchrittDanach konstruiere die beiden Außenwinkelhalbierenden der anderen beiden Winkel. Entscheide, ob man aus folgenden Angaben eindeutig Dreiecke . a) a = 7 cm b = 5 cm γ = 120° b) a = 5 cm b = 4 cm c = 8 cm c) α = 60° β = 25° c = 6 cm.: Abbildung 11: Ankreise Dreieck konstruieren Diese Inhalte gehören zu unserem Bereich Mathematik (Geometrie).

Dreiecke: Berechnungen, Sätze und Konstruktionen online lernen

Beispiel 2: Berechnung des Flächeninhalts.Die SuS können ihre Konstruktionen mit Lösungsfolien abgleichen.Ein Dreieck lässt sich konstruieren, wenn man 3 Bestimmungsstücke kennt.In einem Dreieck kannst du vier Geraden konstruieren, die pro Winkel oder Seite einmal vorkommen. Hinweise: So kannst du die Beschriftung von Objekten anzeigen oder umbennen: Rechtsklick auf die Beschriftung bzw.Außerdem hätten die Punkte nicht mehr die richtige Reihenfolge. Er wird auch Massenmittelpunkt oder physikalischer Schwerpunkt der Dreiecksfläche . ♦ Viereckskonstruktionen Viereckskonstruktion

Ankreise Dreieck: Erklärung, Beweis & Konstruieren

Die Kongruenzsätze zeigen nicht nur, wann zwei Dreiecke kongruent, also deckungsgleich, sind. Winkelsymmetrale des Winkels i . Schwerlinie mit Ecke I .

Dreiecke konstruieren (Kongruenzsatz SsW)

Gib auch den Radius r I des Inkreises an.Wie man ein Dreieck konstruieren (zeichnen) kann, lernt ihr hier. Tauche ein in die Welt der geometrischen Formen und werde zum Dreiecks-Experten! Beliebte Inhalte aus dem Bereich Geometrie Rechtwinkliges Dreieck Dauer: 04:08 .Konstruiere das folgende Dreieck ABC mit a = 5,8 cm, b = 4,5 cm und α = 68°. LÖSUNG: TOP: Aufgabe . a) c = 7 cm; α = 44 0; γ = 70 0 b) b = 6,4 cm; c = 7,2 cm; γ = 100 0 Aufgabe 15: Konstruiere die folgenden Dreiecke mit den Winkelhalbierenden. So wird das Dreieck im Gleichgewicht gehalten. Beschreibe die Form eines . Lerne, Konstruktionssätze anzuwenden und Sachprobleme zu lösen! 1.Aufgabe 3: Konstruiere ein gleichschenklig-rechtwinkliges Dreieck mit der Hypotenuse c=8cm. Bestimme auch die jeweilige Dreiecksart: Gleichseitiges Dreieck, gleichschenkliges Dreieck, . Berechne mit Hilfe deiner Zeichnung den Umfang und die Fläche des Dreiecks. Liegt eine Achsensymmetrie . Ein Dreieck hat eine Höhe von 6 cm und eine Basis von 8 cm.Dreieck konstruieren – Geometrie – Klassenarbeiten.Für alle Dreieckskonstruktionen gilt die folgende (in der Mathematik übliche) Beschriftung! C. F = ½ × a × b.