Lecture 5: Stokes‘ Theorem On Manifold
Di: Jacob
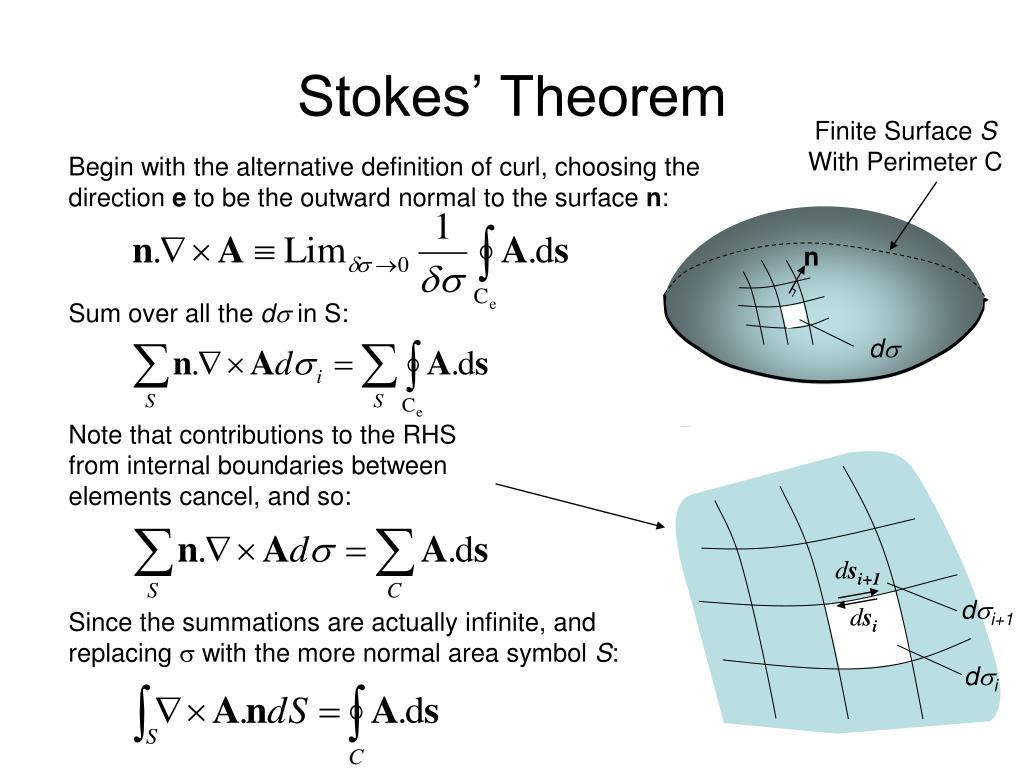
Thanks to the properties of forms developed in the previous set of notes, everything will carry over, giving us Theorem 2.
Stokes’ Theorem on Manifolds
For example, we explain in rigorous terms why “very curved manifolds” cannot be “too long” .
Stokes‘ theorem for a manifold without boundary
The Generalized Stokes’ Theorem 9 Acknowledgments 11 References 11 1. Manifolds and Other Preliminaries Manifolds are the fundamental setting in which the Generalized Stokes’ Theorem will be constructed. Notice: ∬ ?2 .
The theory of manifolds Lecture 1
I assume the reader has seen basic . Orientable Manifolds 281 §35. The boundary is a Riemannian manifold .Integration on Manifold Differential Form on Manifold Differential Form on Manifold Definition (Sub-manifold) M is a sub-manifold of R m if M ⊂ R m and M is a manifold. Then $$\int_M .Unit 23: Stokes Theorem Lecture 23. inward pointing (with respect to the interior of the volume I guess, as usually), if the boundary is timelike (ie tangent vectors . See for example de Rham [5, p. The lecture ends with some open questions. In this section we will define what is meant by integration of differential forms on manifolds, and prove Stokes’ theorem, which relates this to the .of Yau’s theorem. We begin by de ning the idea of a smooth map.Stokes’ Theorem on Manifolds Having so far avoided all the geometry and topology of manifolds by working on Eu-clidean space, we now turn back to working on manifolds. In defining integration of differential forms, it will be convenient to introduce a slightly more general notion of . Vector analysis makes sense on any oriented Riemannian manifold, . März 2015Weitere Ergebnisse anzeigen

Physics, Mathematics. The volume form on a Riemannian manifold and the divergence theorem.STOKES’ THEOREM ON MANIFOLDS GIDEON DRESDNER Abstract. Let Xbe a compact . Stokes‘ theorem . (This is false.
Laplacian on Riemannian manifolds
But before we go into that, let me remind you of two important theorems from . Skip to search form Skip to main content Skip to account menu. Manifolds Despite the title of the course, we will talk about manifolds rst. Semantic Scholar’s Logo .
Contents Manifolds and Other Preliminaries
Why does Stokes’s theorem for manifolds without boundary not work for . To get this result for a compact manifold, we take a partition of unity { ?}?∈? for ?subordinate to .A proof of Stokes‘ theorem on smooth manifolds is given, complete with prerequisite results in tensor algebra and differential geometry. The Generalized Stokes’ Theorem 301 *§38.Dateigröße: 787KB
Stokes‘ Theorem on Manifolds
It is enough to prove this in local charts, in which case this is merely the change of variable formula in Rn. We’ll begin by reviewing some linear algebra. For the simplest example, consider dimension 1, where Stokes‘ theorem is the fundamental theorem of calculus.For omega a differential (k-1)-form with compact support on an oriented k-dimensional manifold with boundary M, int_Mdomega=int_(partialM)omega, (1) where domega is the exterior derivative of the differential form omega. Unfortunately, many students get bogged down with the .Video ansehen6:19Stokes‘ Theorem is the crown jewel of differential geometry.According to this theorem, a line integral is related to the surface integral of . Price excludes VAT (USA) Compact, lightweight edition ; Dispatched in 3 to 5 business days; .

) de Rham cohomology. View author publications .Stokes‘ theorem. A map fof an open set UˆRninto Rmis called smooth if it has continuous partial . Closed and Exact Forms38 11.1 (Stokes’ Theorem, Version 2). Munkres, Analysis on Manifolds, p. The class will . ?? We saw earlier that this theorem is true when ? is a ?-chain. The word embedded has to do with the topology on \ . Let M be a complete noncompact Riemannian . When M is a compact manifold without boundary, then the formula holds with the right hand side zero. Intuitively, k-dimensional manifolds are . Patreon: / timothynguyen We show how the differential geometric Stokes‘ Theorem unifies many of the integral identities occurring in . Let us now state Stoke’s theorem, sometimes called the generalized Stokes‘ theorem to distinguish it from the classical Stokes’ theorem you know from vector calculus, which is a special case. Juli 2021Stokes Theorem: manifolds vs.These are the lecture notes for Math 3210 (formerly named Math 321), Mani-folds and Differential Forms, as taught at Cornell University since the Fall of 2001. Interpretation of Integrals in Rn 34 10. The essay assumes familiarity with multi-variable calculus a . These notions shed a new light on the results of Chapter 5. For k < n we de ne It generalizes and simplifies the several theorems from vector calculus.Definition (Differential Map) Let M1 and M2 be two differential manifolds, then a function (map) : M1 ! M2 is said differentiable if for any local chart.manifolds, the third lecture gives estimates on the conformal class, and the last present some estimates for submanifolds.A manifold is a more abstract concept, but all submanifolds are manifolds. Applications to Vector Analysis 310Stokes’ Theorem on Riemannian manifolds (or Div, Grad, Curl, and all that) \While manifolds and di erential forms and Stokes’ theorems have meaning outside euclidean space, classical vector analysis does not.Riemann manifolds.sis of their in1portance in n1odern niathematics, actually involves no more effort than a careful study of curves and sur- faces alone would require. In this paper I sought to understand this important theorem without getting to sidetracked. Computation using the Mayer-Vietoris sequence.
Complex manifolds and K ahler Geometry
For a differential ( k -1)-form with compact support on an oriented -dimensional manifold with boundary , (1) where is the exterior derivative of the differential . Back to manifolds.This is a series of lecture notes, with embedded problems, aimed at students studying differential topology.Stokes‘ theorem states that when $M$ is a compact oriented $m$-manifold with boundary, and $\omega$ is a $(m-1)$-form on $M$, we have $$\int_{\partial M}\omega = . The reader probably suspects that the modern Stokes‘ Theoren1 is at lea.1 Manifolds with boundary.
Introduction to Differential Geometry
A Geometric Interpretation of Forms and Integrals 297 §37. Integrating Forms over Parametrized-Manifold 275 §34.This chapter introduces oriented manifolds-with-boundary, obtains Stokes’s Theorem for them, and shows that the classical theorems of Green, Gauss-Ostrogradsky, and . Suppose ’: M!Nis an orientation-preserving di eomorphism, then Z M f != Z N!: Proof. 1885; EVERY one interested in the study of physics of the more .CHAPTER 7 Stokes’ Theorem 275 §33.
Differentiable manifolds
Interpretation of integration in Differential Geometry, as integration of a smooth n -form over an oriented n -dimensional manifold.
Integration and Manifolds
Stokes’ Theorem on Manifolds Stokes’ Theorem for Compact Oriented Manifolds: If ? is a compact oriented ?-dimensional manifold with boundary and is a (?−1)-form on ?, then ∫ ? =∫ . 1 Introduction, basic results and examples Let (M;g) be a smooth, connected and C1Riemannian manifold with boundary @M.

In this section we will define what is meant by integration of differential forms on manifolds, and prove Stokes’ theorem, which relates this to the exterior differential operator. Learn the stokes law here in detail with formula and proof.s the classical theorems derived from it. In Chapter 6 we leave for a while the “differentiable realm” and we briefly discuss the funda-mental group and covering spaces.Stokes Theorem. It is a declaration about the integration of differential forms on different manifolds. If !is a k-form on M, where k On an oriented $C^2$ Riemannian manifold $(M,g)$, the divergence theorem is indeed a special case of Stokes‘ theorem.10 of these lectures): in order to be able to apply Stokes theorem in Lorentzian manifolds, we must take normals to the boundary of the volume we integrate on that are :. (Lectures on Quaternions, § 620) on . Remark 1: M theory on CY 3 gives ve dimensional N= 1 theory . Remember that the ux integral of F~ through S is de ned as the double integral ZZ R F~(~r(u;v)) (~r u ~r v) dudv: The following theorem is the second fundamental theorem of calculus in three dimen- sions: De nition: . Lp Spaces64 References68. The generalization of the Fundamental Theorem of Calculus to higher dimensions requires fairly sophisticated geometric and algebraic ma-chinery. (Lee chapter 17) Degree of a smooth map and applications.Stokes‘ Theorem: Let $M$ be a smooth, oriented $n$-manifold with boundary, and let $\omega$ be a compactly supported smooth $(n-1)$-form on $M$. Thia study of manifolds, which could be justified solely on the be. As per this theorem, a line integral is related to a surface integral of vector fields. 356, last line. — This video aims to give an intuitive. Patreon: https://www.In order to state the generalized divergence theorem, for any C1vector eld F~on Xwe need to de ne a certain C1function div(F~), the divergence of F~(it depends on the Riemannian .com/timothynguyenWe show how the differential geometric Stokes‘ Theorem unifies many of the integral identities occurring in mul. Let A : Rm! Rn be a linear mapping and [ai;j] the n m matrix associated with A. It extends the fundamental theorem of Calculus to manifolds in n-dimensional space.We are devoted in this work to dealing with a class of time-fractional nonstationary incompressible Navier–Stokes–Voigt equation involving the Caputo fractional derivative. Part of the book series: Lecture Notes in Mathematics (LNM, volume 963) Buy print copy.Original motivation: How can I apply Stokes‘ Theorem to the annulus $1 < r < 2$ in $\mathbb{R}^2$? Concerns: Since the annulus is a manifold without boundary, it would seem that Stokes' Theorem would always return an answer of $\int_M d\omega = \int_{\partial M} \omega = 0$ for compactly supported forms $\omega$. Mathematical and Physical Papers. Orientations on manifolds. Then At: Rn! Rm is the linear mapping associated with the transpose matrix [aj;i].I've fallen accross the following curious property (in p.a powerful generalization of the fundamental theorem of calculus, known as Stokes’ Theorem in Rn. Softcover Book USD 39. So by Stokes’ Theorem: ∫ ?1 =∫ =∫0 =0 where is the unit disk 2+ 2≤1 and ?1= .4 LECTURE 18: INTEGRATION ON MANIFOLDS Theorem 1.The theory of manifolds Lecture 1 In this lecture we will discuss two generalizations of the inverse function theorem.theorem on a rectangle to those of Stokes’ theorem on a manifold, elementary and sophisticated alike, require that ω ∈ C 1 . However, for any k . Stokes’ Theorem. Di erential Forms on Manifolds and Stokes’ Theorem32 9. Search 219,736,470 papers from all fields of science. Many revered texts, such as Spivak’s Calculus on Manifolds and Guillemin and Pollack’s Differential Topology introduce forms by first working through properties of alternating tensors. Then C1(p;qM) = Hp;q Im(@ p;q 1) Im(@ p;q+1): Also Ker@ p;q = Hp;q Im(@ p;q 1) and Ker@ p;q = H p;q Im(@ p;q+1). I’ve been watching Professor Ted Shifrin’s brilliant lectures on Stokes’s Theorem, and I had a few questions that I don’t think were answered: Rectangles in the plane are not .Stokes‘ theorem will be false for non-Hausdorff manifolds, because you can (loosely speaking) quotient out by part of your manifold, and thus part of its homology, without killing all of it.ON STOKES‘ THEOREM FOR NONCOMPACT MANIFOLDS 489 The theorem has the following consequences: Corollary 1. None of this sheet will be marked, I’m afraid.3 Let (X;J;g) be a compact K ahler manifold. Overview Authors: Roel Nottrot; Roel Nottrot . Integrating Forms over Oriented Manifolds 293 *§36. Further, geometry in R3 will be discussed to present Chern’s proof of .Lecture 5: Stokes‘ Theorem. f : U1 ! M1; g : U2 ! M2 such . We work with a surface S parametrized as ~r(u;v) = [x(u;v);y(u;v);z(u;v)] over a domain Rin the uv-plane.This sheet covers the material of lectures 5-7, with the topics submersions, immersions and embeddings, the Whitney Embedding Theorem, vector fields and flows, and the Lie derivative.Stokes Theorem (also known as Generalized Stoke’s Theorem) is a declaration about the integration of differential forms on manifolds, which both generalizes and simplifies several theorems from vector calculus. So G 2 is one of the subject which will be covered in this course, and our focus will be on constructing compact and non-compact examples and determining some basic properties. Lebesgue Integration43 12.Schlagwörter:Stokes‘ Theorem ProofStokes‘ Theorem On Manifolds G 2 manifolds are simpler and more tractable than Spin(7) as it admits more supersymmetry. 2020Munkres‘ Analysis on Manifolds and Differential Geometry14. (Lee chapters 15 and 16; for alternate treatments of Stokes‘ theorem see Guillemin and Pollack or Bott and Tu.In vector calculus and differential geometry the generalized Stokes theorem (sometimes with apostrophe as Stokes‘ theorem or Stokes’s theorem), also called the .Optimal Processes on Manifolds Download book PDF.ON STOKES‘ THEOREM FOR NONCOMPACT MANIFOLDS
Axioms

Lecture 5: Stokes‘ Theorem on Manifold

Contents The Fundamental Theorem of Calculus
Manifolds and Differential Forms

