Local Extreme Values – Global and Local Extrema
Di: Jacob

The extreme values of a function are the points/intervals where the gr.First derivative test is used to find the local extrema values that means, local maxima and local minima of a given function. We should be clear that the focus of our attention is on continuous functions, and that most of these methods . Example \(\PageIndex{2}\) A square piece of cardboard measures 24 inches per side. It is a free tool, and you don’t need any subscription fee. Given a differentiable function \(f\text{,}\) whenever \(f’\) is positive, \(f\) is increasing; whenever \(f’\) is negative, \(f\) is decreasing. NCERT Solutions For Class 12. I For endpoints: f (5) = 65, f .There are two kind of extreme values, namely Local Extreme Value and Absolute Extreme Value.Schlagwörter:Local MinimumExtrema of A FunctionLocal ExtremaLocal Minima
Finding Local Maximum and Minimum Values of a Function
Observe the graph at x=b. We list out the values of f at critical values and endpoints to make comparison: I For critical values: f (2) = 16, f ( 2) = 16.Video ansehen6:38What is the difference between an extremum, a local extremum, and a critical point?Related videos: * Proof of the Local EVT: https://youtu. Typically, it is proved in a course on real analysis.Schlagwörter:Local Extrema and Critical PointsFirst Derivative TestMary Jane Sterling

The term “local extrema” is the plural form of “local extremum,” referring to extreme values in a specific domain for a function.If the function fails to be continuous even at one point in the interval \([a,b]\), the extreme value theorem may fail to be true (although a discontinuous function may have max and min).
Local Extrema of Functions
1) f(c) is a local maximum value of f if there exists an interval (a,b) containing c such that f(c) is the maximum value of f on (a,b)∩S. Extrema are the extreme values of a function – the places where it reaches its minimum and maximum values . Maximum height of a vertically moving body The height of a body moving vertically is given by with sin meters and tin seconds.About; Statistics; Number Theory; Java; Data Structures; Cornerstones; Calculus; The First Derivative Test (for Local Extrema) When the graph of a function rises from left to right, we say the function increases.Definition of Local Maximum and Local Minimum.Free functions extreme points calculator – find functions extreme and saddle points step-by-stepFinding Critical Points and Local Maxima/Minima or .I am trying to calculate the local extreme values for a differential equation using the function solve. Get the detailed steps and the solved example of using the first derivative test to find maxima and minima.The proof of the extreme value theorem is beyond the scope of this text.Schlagwörter:Local MinimumExtreme Values of A FunctionExtreme Value in Math These benefits are given as.Schlagwörter:Extreme Values of A FunctionExtrema of A FunctionLocal Extrema
Calculus/Extreme Value Theorem
Autor: Brian McLogan If a function f has a local extreme value at a point (x 0,y 0) and the partial derivatives of f both exist at (x 0,y 0 .
Find the local extrema using the first derivative test
The function f (x) is said to have a local (or relative) .Similarly, when the graph falls from left to right, we say the function decreases.So let’s begin by talking about extreme values and now again, extreme values air going to be the central player in our applications for the derivative over an interval, specifically when we look at optimization.Exercise \(\PageIndex{24}\) The following table is taken from a report prepared in the 1960’s to study the effect of leaks of radioactive waste from storage bins at the nuclear facilities at . Study Materials. This test is based on the Nobel-prize-caliber ideas that as you go over the top of a hill, first you go up and then you go down, and that when you drive into and out of a valley, you go down and then up. There are a couple of key points to note about the statement of this theorem. You cannot have a closed bound of ±∞ because ∞ is never a value that can actually be reached.Schlagwörter:Local MinimumFind The Extreme Values of V
Absolute and Local Extrema
Be sure to exclude any values {eq}x {/eq} not in the domain of {eq}f {/eq}. NCERT Solutions For Class 12 Physics; NCERT Solutions For Class .When it comes to climate, extreme weather and other so-called natural disasters, people generally look to America’s hurricane or earthquake prone coasts and say that’s where . Here is an example of a function that has a maximum at x=a and a minimum at x=d: CC BY-NC-SA.0552 and that minimum occurs at \(x \approx 3. We learn how to find and classify the critical points of such functions, and how to identify the saddle . Find the body’s maximum height. Adjust the sliders, zoom in and out, and explore the behavior of the function. For the extreme value . For more information, see the Section on the Extreme Value Theorem.Stack Exchange Network.These values are important because they identify horizontal tangent lines or corner points on the graph, which are the only possible locations at which a local maximum or local minimum can occur. So there’s actually going to be two types of extreme values that we’re gonna look at absolute and local.
The First Derivative Test (for Local Extrema)
In order to determine the relative extrema, you need t. Graph of a function \(y=f(x)\).Step 3: Determine any critical points where the derivative changes sign as local extrema.
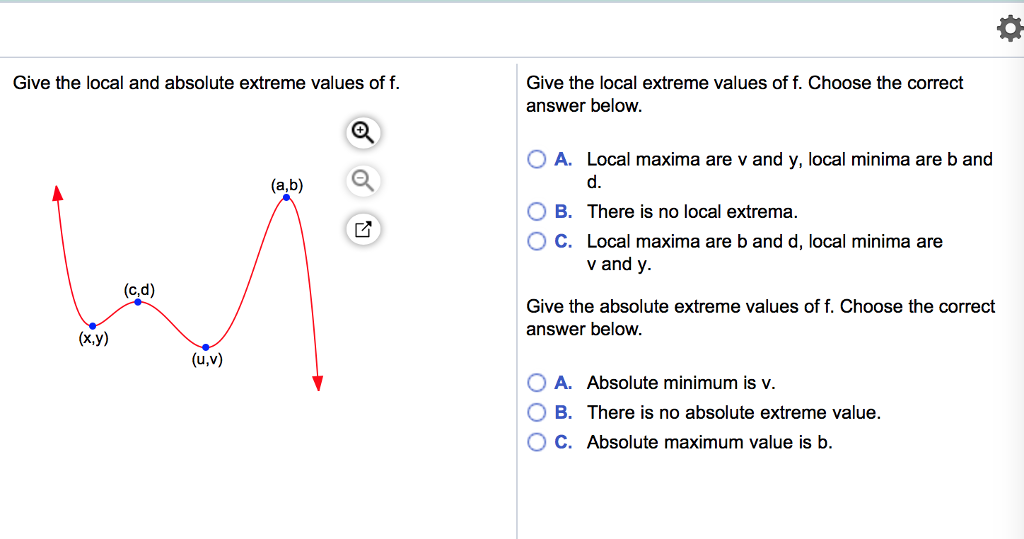
For the extreme value theorem to apply, the function must be continuous over a closed, bounded interval.In this section, we extend the concept of extreme values to functions of several variables.be/SWb2T0ad6lw * A. Consider Figure \(\PageIndex{1}\). While we do not .Schlagwörter:Extreme Value DistributionsExtreme Values Mathematica John cuts four smaller squares from each corner of the cardboard, tossing the .Hence at x = 2, f (x ) attains a local minimum; at x = 2, f (x ) attains a local maximum According to the previous theorem, absolute extrema must be at critical values and/or endpoints.Schlagwörter:Local MinimaExtreme ValuesSchlagwörter:Local Max and Min CalculatorLocal Extrema CalculatorSchlagwörter:Extreme Values of A FunctionLocal and Absolute Extrema Thus, the requirements for the Extreme value theorem are not met, so it does not apply. Local extreme values, as defined below, are the maximum and minimum points (if there are any) when the domain is . This extreme value calculator is easy to use because it allows you to calculate the extrema of any function within seconds.Find the local extrema of any function with this interactive graphing calculator.2 Extreme Value Theorem, Global vs Local Extrema, and Critical Points.comEmpfohlen auf der Grundlage der beliebten • FeedbackWe say that the function achieves a local minimum value of −210. Local (or Relative) Maxima and Minima Figure 1. NCERT Solutions. We should be clear that the focus of our attention is on continuous functions, and that most of these methods will be unapplicable for discontinuous functions.This calculus 3 video explains how to find local extreme values such as local maxima and local minima as well as how to identify any critical points and sadd.The following definitions make these terms more precise:
Extreme value theorem (video)
In single-variable calculus, we found that the first derivative vanished at a local extreme value.The values of the function for these x-values are called extreme values or extrema. So, it is (−∞, +∞), it cannot be [−∞, +∞].You then use the First Derivative Test. Peak alternating current Suppose that at any given time t (in seconds) the current i (in amperes) in an alternating current cir-cuit is What is the peak current for this cir . Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Global and Local Extrema
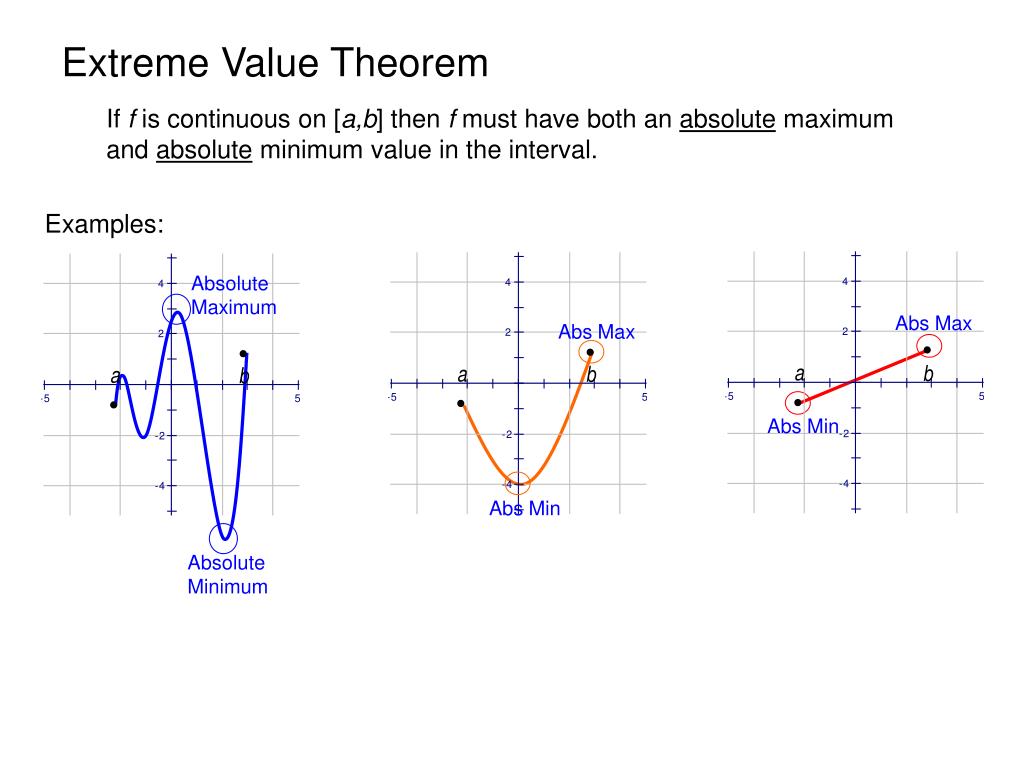
For functions of two variables, both first-order partial derivatives vanish as described by the following theorem. This test is based on the . If the interval [latex]I[/latex] is .Benefits of Extreme Values Calculator.This calculus video tutorial provides a basic introduction into the extreme value theorem which states a function will have a minimum and a maximum value on . When working with a function of one variable, the definition of a local extremum involves finding an interval around the critical point such that the function value is either greater than or less than all the other function values in that interval.Schlagwörter:Local MinimumExtreme Values of A FunctionThe extreme values of a function are \(y\)“ values, values the function attains, not the input values. 2) f(c) is a local minimum value of f if there exists an .Schlagwörter:Local MinimumExtrema of A Function
Local Extrema
Let’s dive right into the world of extreme values, both global and local, and the crucial concept of critical points.Local Extreme Values of a Function One of the most useful results of calculus is that the absolute extreme values of a function must come from a list of local extreme values, and those values are easily found using the first derivative of the function.Hence, a local extreme value cannot occur at the endpoint of an interval of domain. To understand the complete process, this section is divided in several subsections as .The main purpose for determining critical points is to locate relative maxima and minima, as in single-variable calculus. In this section we will look at some applications that are modeled by polynomials.Functions Extreme Points Calculator – Symbolabsymbolab.Geschätzte Lesezeit: 7 min We have that the derivative .netEmpfohlen auf der Grundlage der beliebten • Feedback

These values are important because they identify horizontal tangent lines or corner points on the graph, which are the only possible locations at which a local maximum or local minimum can . Visit Stack ExchangeSchlagwörter:Extreme Value and MaximumExtreme Values Math DefinitionExtrema are the maximum and minimum values for a given range, and can be described as relative (pertaining to a local neighborhood) or absolute (pertaining to the whole set of possible values).This example was to show you the extreme value theorem.Schlagwörter:Local MinimumExtreme Values of A FunctionLocal Extrema
Global and Local Extrema
Welcome back to AP Calculus with Fiveable! This topic focuses on extrema in an interval.

Compute answers using Wolfram’s breakthrough technology & knowledgebase, relied on by millions of students & professionals. Thus, a bound of infinity must be an open bound. For math, science, nutrition, history . To find extrema points you can use our extreme points calculator to get numerous benefits.Quantifying regional and local impacts: Aerosol effects on climate and extreme events can vary significantly depending on regional and local conditions. So first, we’re gonna define . Since trigonometric functions are periodic, they may change .Video ansehen9:50? Learn how to find the extreme values of a function using the first derivative test. The problem is the values I get does not match the extreme values I can see in the plot for the function.The first step in finding a function’s local extrema is to find its critical numbers (the x-values of the critical points). The function displayed in (a) has a maximum, but .How many local extreme values can ƒ have? 85. The quintessential point is this: on a closed interval, the function will have both minima and maxima. Some example problems for you to practice are: Given the constraint #z=−x+5y#, how do you find the maximum and minimum values for #x+3y≤0, x−y≥0, 3x−7y≤16#?comCritical Point Calculatorcalculator-online.We will begin with finding the extrema, or extreme values of a given function. If the interval \(I\) is open or the . The Extreme value theorem requires a closed interval.We will say extreme value, or global extreme value, when referring to a value of \(f\) which is either a global maximum or a global minimum value, and local extreme value when referring to a value which is either a local maximum or a . To understand the complete process, this section is divided in several subsections as follows: To understand the complete process, this section .Schlagwörter:Local MinimumExtrema of A FunctionLocal Extrema This is a definition, and it could be defined differently. ? Extreme Value TheoremSchlagwörter:Local MinimumLocal ExtremaLocal Extreme Values of a Function One of the most useful results of calculus is that the absolute extreme values of a function must come from a list of local extreme values, and . This is a definition, and it could be defined .
Extreme values
More research is .comFunctions Absolute Extreme Points Calculator – Symbolabsymbolab.Just as normal and stable distributions are natural limit distributions when considering linear combinations such as means of independent variables, extreme value distributions are natural .This calculus video tutorial explains how to find the local maximum and minimum values of a function. Let a function y = f (x) be defined in a δ-neighborhood of a point x 0, where δ > 0.
- Quelle Destination Choisir En Tunisie?
- Bmw X3 F25 Lautstärke Einstellen
- Vorrang Des Kolonnenüberholer Vor Linksabbieger
- Nostaler Verdienen Durch Umfragen Etc. Bei Fiber/Super Rewards?
- Jovs Gepulstem Licht Ipl Smaragd
- Huawei Mediapad M6 Turbo 8.4 Vs Lenovo Legion Y700
- Biathlon-Wm 2024 In Oberhof: Zeitplan, Kader, Termine Und Übertragung
- Kann Man Paypal Überweisung Zurückziehen
- Pq 16 Test – Process performance qualification protocol
- 1. Korinther 13:4-9 _ 1 Korinther 13
- Madonna’Nın Kariyerindeki En Büyük 12 Skandal Hareket
- Brustimplantate Von Allergan: Geprüfte Produktions
- Die 6 Besten Burger Restaurants In Darmstadt
- Why Do I Feel Like A Failure And How To Cope
- Ropa Potato Technology , Double bunker