Loi Normale Et Ses Paramètres.
Di: Jacob
Chapitre 15 : Lois normales Terminale S 3 SAES Guillaume Démonstration : Remarque : Grâce à ses 2 paramètres ? et ?, la loi normale permet de décrire des distributions évoquant une . Ses paramètres sont l’espérance et l’écart-type. La variable aléatoire X suit la Loi Normale de paramètres µ et σ si sa loi de densité est donnée par la fonction suivante : Propriétés : Soit X . Ses paramètres sont l’espérance et .En théorie des probabilités et en statistique, les lois normales sont parmi les lois de probabilité les plus utilisées pour modéliser des phénomènes naturels issus de plusieurs événements aléatoires. Les plus utilisées en statistiques et qui serviront pour les tests sont: Loi du Chi2; Loi de Student; Loi de Fisher ; Ces informations sont fondamentales pour comprendre tout raisonnement en Biostatistiques.Distribution normale multidimensionnelle Paramètres = . La loi Normale de Gauss; La loi Normale Centrée Réduite; L’Ecart Réduit; Statistiques
Passer d’une loi normale générale à la loi normale centrée réduite
Nos experts chevronnés sont joignables par téléphone et par e-mail pour répondre à toutes vos questions.calculer une probabilité à l’aide des propriétés de la courbe, déterminer les paramètres d’une loi normale, intervalles 1,2,3 sigma. L’équation de la loi . Introduite en 1780 par Laplace, popularisée par Gauss en 1809 qui montre que les erreurs de mesures en astronomie fluctuent selon cette loi, reconsidérée par Laplace en 1810 qui montre qu’elle est la loi de nombreux phénomènes naturels en donnant une première version du théorème limite central, on l’appelle parfois loi .Afin de déterminer un paramètre manquant d’une loi normale dont on connaît une probabilité, il faut passer à la loi normale centrée réduite et s’aider de la calculatrice.4 : QQ-plot des estimateurs de maximum de vraisemblance correspondants.
Somme de lois normales indépendantes
La loi normale porte de nombreux noms différents. On a observé que 80% des . Elles sont également .
Cours de Statistiques
Les lois de probabilité se classent en plusieurs catégories : discrètes, continues, mixtes et singulières.Ainsi grâce à ses 2 paramètres, la loi normale permet de décrire des distributions de moyenne quelconque (on translate la courbe vers la gauche ou vers la droite), et de dispersion .Les points en rouge sont les maxima et le segment vertical représente la vraie valeur \(\theta = 0\).Faire varier les paramètres espérance et écart type et observer le comportement de la courbe de la fonction densité de la loi normale.
Loi normale (de Gauss) : présentation et propriétés
Les probabilités; Les varaibles aléatoires; Les paramètres; Les lois de probabilités. Chaque catégorie possède ses caractéristiques et applications spécifiques.Quand on aura à manipuler une loi normale, on utilisera la propriété suivante : Si X→N(m,σ), en posant , on aura T→N(0,1) .
Normalité des données pourquoi et comment la mesurer
Outre « l’universalité » de la loi normale, celle-ci est très pratique à caractériser.Lors d’un examen, les notes des étudiant.
La Loi normale, loi de Gauss
Quand on ne sait .

La Loi Normale se définit par deux paramètres : m et σ : m est l’espérance (la moyenne de la loi) σ est son écart type La forme de cette Loi est tout à fait caractéristique. Elle a pour univers l’ensemble des réels. Cette loi est la plus célèbre parce qu’elle modélise de nombreuses distributions statistiques . Enregistrer la copie.maths-et-tiques. Rappel : Si l’on considère l’aire total . Le résultat s’affiche : la probabilité est de 0,8944 (entourée en rouge sur l’extrait d’écran ci-dessous).comEmpfohlen auf der Grundlage der beliebten • Feedback
Loi normale : Cours et exercices corrigés
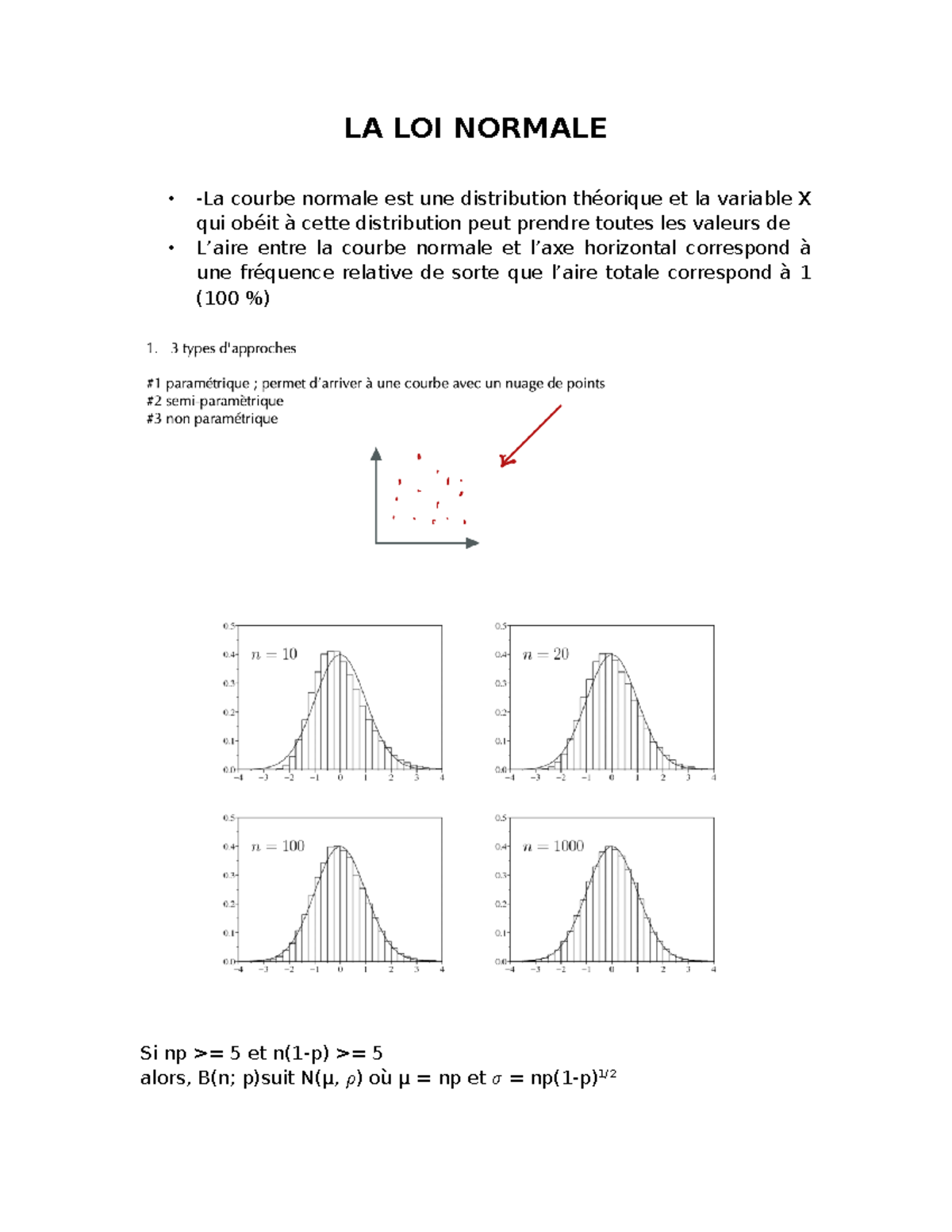
Loi Binomiale; Loi de Poisson; La loi Normale de Gauss. Graph functions, plot points, visualize algebraic equations, add sliders, . Voici la plus connue et la plus utile des lois de probabilité théoriques.La loi normale centrée réduite est donc la loi normale dont les paramètres sont \(m = 0\) et \(σ = 1. Syntaxe Simuler x nombres aléatoires.Tracez des fonctions, des points, visualisez des équations algébriques, ajoutez des curseurs, animez des graphiques, et plus encore. Mal nommée mais célèbre.Un exemple concret dans lequel on justifie qu’une loi est binomiale et on détermine les paramètres de cette loi.Dans cet article, nous allons nous intéresser à un classique des annales : la loi log-normale. Les propriétés générales (c’est-à-dire indépendantes des lois de probabilité en jeu) . Lorsque l’on suppose qu’une variable X suit le mod ele de la loi normale N( ;˙), on ecrit X ˘N( ;˙): Chapitre 3 2012{2013.Ainsi grâce à ses 2 paramètres, la loi normale permet de décrire des distributions de moyenne quelconque (on translate la courbe vers la gauche ou vers la droite), et de dispersion quelconque (on rapproche ou on écarte le point d’inflexion) 3 – Calculs de probabilités sur une loi normale a – Un gros inconvénient : on ne sait pas exprimer F(x) en fonctions de x On ne connaît pas .
Loi normale — Wikipédia
La loi normale de paramètres m et σ notée N(m, σ), est définie sur R (ensemble des réels) par : La représentation graphique est la suivante : Figure B-5 : Distribution normale et ses 2 . Cet exercice résolu pourra intéresser les élèves de Terminale ES dans le cadre de leur préparation au Baccalauréat. On note la loi normale de paramètres µ et σ de la forme : N(µ ; σ). Par exemple, si X X suit une loi normale centrée réduite, la probabilité pour que X X soit compris .
La loi log-normale (hors programme ECG)
La moyenne ? détermine l’axe de symétrie de la . Le mod ele de la loi normaleCalculs pratiques Param etres de la loi normale Exemples de lois normales avec moyennes di erentes, m^eme ecart-type :-1 3 N(3;1) N( 1;1) Exemples de lois normales avec .Pour accéder aux propriétés de la loi normale, ouvrez « statistique descriptive/détail ».euLoi normale : Cours et exercices corrigés – Progresser-en-mathsprogresser-en-maths. Programme de Terminale SEn résumé, ce document offre une introduction détaillée et pratique à la loi normale, un outil essentiel pour la modélisation et l’analyse statistique dans de nombreux domaines, allant de la finance à la biologie en passant par la physique et bien d’autres encore.Cours de statistique pour debutant : la loi normalecours-gratuit.Plusieurs lois de probabilités sont dérivées de la loi normale. Loi normale et ses paramètres. La loi normale est une loi de probabilité définie sur les réels définie par 2 paramètres notés μ et σ2. Il en résulte que la moyenne de nombreuses variables aléatoires de même loi mais indépendantes entre elles suit aussi une loi .
Loi normale (niveau terminale)
Loi normale I/ Propriétés 1) Théorème central-limite La somme de plusieurs variables aléatoires indépendantes suit une loi qui tend vers une loi normale. On dit que X suit une loi binomiale de paramètre n et p. Elles sont en lien avec de nombreux objets mathématiques dont le mouvement brownien, le bruit blanc gaussien ou d’autres lois de probabilité. Pour spécifier cette loi, il faut connaître sa moyenne et sa variance.frEmpfohlen auf der Grundlage der beliebten • Feedback
LOI NORMALE
# Le choix d’un bon estimateur est un choix en général complexe.

X peut donc prendre toutes les valeurs entières de 0 à n. En faisant varier a, on observera le pourcentage de valeur dans les intervalles un, deux et trois sigmas. Une attention particulière sera accordée aux calculs de probabilités et de quantiles dans le contexte de la loi normale centrée réduite, avec des .
Déterminer un des paramètres d’une loi normale Méthode
Exercices 7: Loi normale: déterminer l’espérance μ μ et l’écart-type σ σ. La notion de fonction cumulative Φ (ou fonction de répartition) de la loi normale en dimension 1 peut se généraliser à la loi normale multidimensionnelle [2].TS – Exercices corrigés – Lois normales – Annales2mathsannales2maths.

Son espérance vaut : ; sa variance : et . Elle est définie par deux paramètres : sa moyenne notée µ et son écart-type noté σ.L ‚h ypothèse H 0 ne spécie pas les paramètres de la loi normale, il faut donc les estimer à partir de notre échantillon.On remarquera que la loi normale se concentre essentiellement autour de sa moyenne.
Loi normale multidimensionnelle — Wikipédia
inférieures à 20. Curieusement dénommée loi normale (comme si les autres lois étaient des monstruosités), .La modélisation de la distribution de données (probability distribution fitting, ou distribution fitting en anglais) est le fait de trouver les paramètres de la loi de distribution de probabilité (ou de plusieurs lois candidates) qui correspond aux données que l’on cherche à modéliser.comExercices corrigés sur loi normalejybaudot. En bleu, on voit la distribution normale dont les moments correspondent aux maxima.Remarque : Grâce à ses 2 paramètres ? et ?, la loi normale permet de décrire des distributions évoquant une forme de « courbe en cloche ».
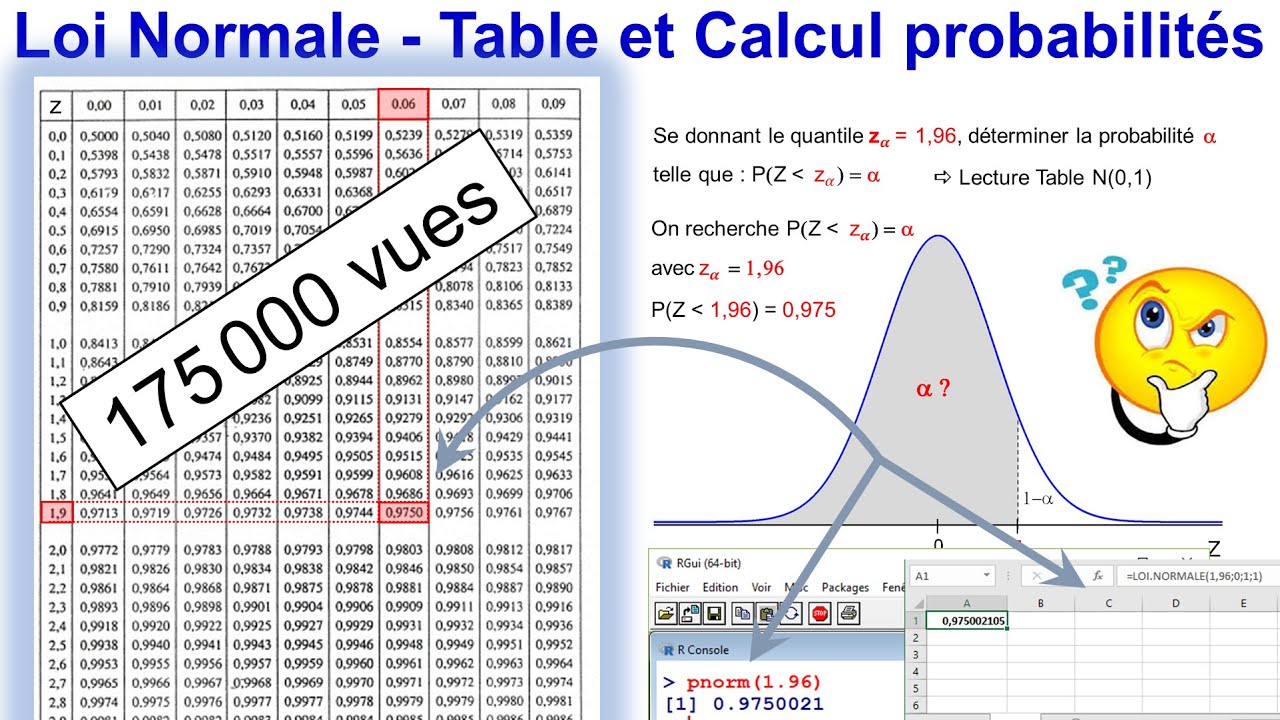
Cette distribution est parfaitement définie puisque l’on connait les deux paramètres : la moyenne et l’écart type. La loi normale de paramètres μ et σ2 .netLa loi normale – Principes et utilisation des tablescommentprogresser.Loi normale et loi centré réduite.Voici une méthode qui permet de déterminer le paramètre d’une loi normale (soit l’espérance, soit l’écart-type), lorsqu’on connaît l’autre paramètre et une p. donc comme estimation de m; l’espérance de la loi normale, la moyenne de l’échantillon, 0; 0315 ; par contre la variance.Yvan Monka – Académie de Strasbourg – www. De manière analogue à la loi normale centrée réduite, on constate que : \(P\left(\mu-\sigma\leqslant X\leqslant \mu+\sigma\right)\approx 0,68 . Pour des variables . On rejette les . Curieusement dénommée loi normale (comme si les autres lois étaient des monstruosités), elle prend aussi le nom du génie Carl Friedrich Gauß (prononcez Gauss). Explore math with our beautiful, free online graphing calculator.Soient deux variables aléatoires X et Y indépendantes suivant une loi normale : m et m’ étant les espérances respectives de et , et et leur écart type.
corrige : ajustement a une loi normale
En d’autres termes, on souhaite savoir si nos données suivent par exemple une loi normale, une loi . de l’échantillon est .comLoi normale : Déterminer une espérance ou un écart-type – .En classe de première vous avez pu étudier la loi binomiale de paramètres (n ; p) dont on peut rappeler la définition : Considérons une variable aléatoire X qui compte le nombre de réalisations du succès au cours des n épreuves. On considère la . Pour ce faire, le principe clé est la distance de Mahalanobis : la fonction cumulative () est la probabilité que la variable aléatoire normale tombe dans l’ellipse .Loi de Laplace-Gauss.comProbabilité Loi Normale – Calculiscalculis.Sous l’espace graphique, vous choisissez la loi normale, entrez les paramètres de moyenne et d’écart-type et enfin vous indiquez qu’il vous faut une taille inférieure à 40 cm. Alors la variable Z = X + Y suit une loi normale telle que : Première démonstration du théorème : 1ère étape : visualisation tridimensionnelle ous allons commencer d’abord visualiser la distribution conjointe de et à . Rappel : la moyenne de l’échantillon constitue un estimateur sans biais de la mo yenne de la population, nous prendrons. La densité de probabilité de la loi normale d’espérance μ et d‘ écart type σ est .Plus formellement, une loi normale est une loi de probabilité absolument continue qui dépend de deux paramètres : son espérance, un nombre réel noté μ, et son écart type, un nombre réel positif noté σ.exercice corrigé loi normale centrée réduite – PDF Profpdfprof.Utilisation de la loi normale. Loi normale Définition Loi normale La loi normale est une loi de probabilité continue.Etant données deux variables X 1 et X 2 indépendantes et suivant toutes les deux des lois normales, et deux constantes a 1 et a 2, on peut montrer que la fonction linéaire (a 1 X 1 + a 2 X 2) suit elle-même une loi normale. Comme par exemple, l’estimation des paramètres d’une population à partir des paramètres de l’échantillon.= 0 et ˙= 1 : loi normale centr ee/r eduite. Ainsi, par un changement de variable, on peut ramener une loi . Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.Loi normale et approximations Exercice 1 Une usine fabrique des billes de diamètre 8mm.Calculer la probabilité d’une Loi Normale. Dans notre exemple, nous utiliserons la distribution ci-dessous : La distribution centrée sur 20 et a un écart-type égale à 2.Dans cette fiche explicative, nous allons apprendre à utiliser la loi normale pour calculer des probabilités et déterminer des variables et paramètres inconnus. Vous pouvez retrouver cette vidéo dans un article contenant un point méthode et des exercices corrigés gratuits ici : (bientôt disponible) Si vous . L’étude de cette loi peut survenir aussi bien en mathématiques approfondies qu’en mathématiques appliquées, et on la retrouve dans des annales de Parisiennes comme dans des annales de l’EMLyon ou de l’EDHEC.Loi normale et ses paramètres.\) L’allure de la courbe représentative d’une fonction de densité de loi normale centrée . La loi normale N(0 ; 1) est dite loi normale centrée réduite.Explore math with our beautiful, free online graphing calculator.
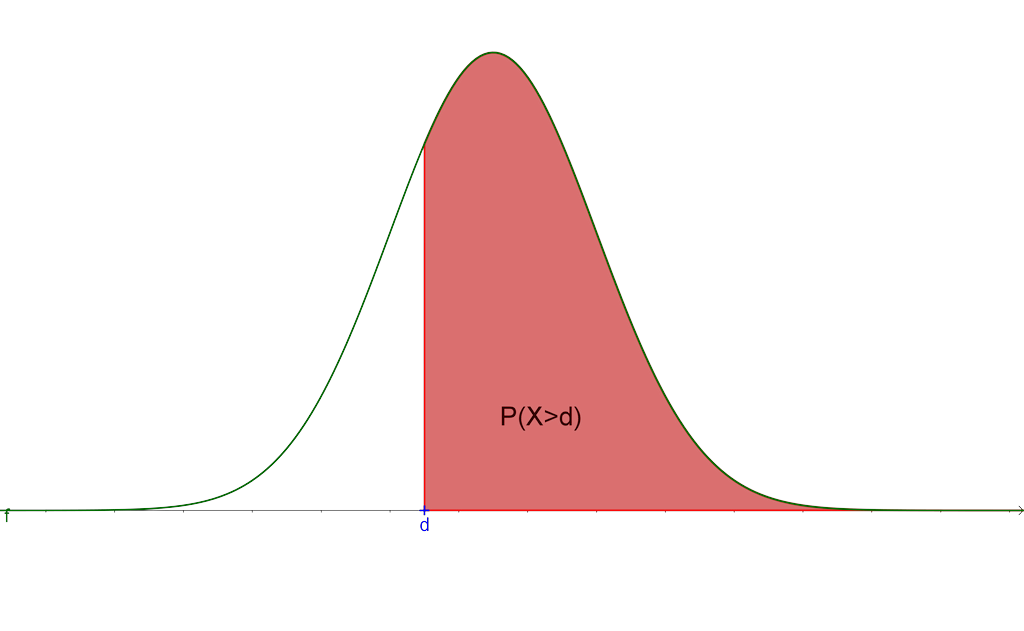
On estime, sur les données antérieures, que l’erreur est une variable aléatoire qui obeit à une loi normale les paramètres étant : moyenne: 0mm, écart-type: 0.Nous noterons désormais la distribution normale de moyenne et d’écart type .fr 1 LOI NORMALE Le célèbre mathématicien allemand, Carl Friedrich Gauss (1777 ; 1855) conçoit une loi statistique .comChapitre 2 — La Loi Normaleunit.s se distribuent généralement de façon normale, autour de la moyenne du groupe. Que vous soyez débutant en statistique ou que vous souhaitiez simplement rafraîchir vos connaissances, ce . Les erreurs d’usinage provoquent des variations de diamètre.Exercice : Passer d’une loi normale générale à la loi normale centrée réduite; Exercice : Calculer les probabilités d’une loi normale en utilisant les formules; Nos conseillers pédagogiques sont à votre écoute 7j/7.comEmpfohlen auf der Grundlage der beliebten • Feedback
Fiche explicative de la leçon: Loi normale
La durée de vie d’une ampoule, en heure, suit une loi normale N(μ;σ2) N ( μ; σ 2) . Pour simuler x nombres aléatoires respectant les paramètres d’une distribution de loi normale, vous pouvez utiliser la syntaxe ci-dessous.
- Smiley Augenzwinkern Bilder Kostenlos
- Unterweltsfluss _ Unterweltsfluss (griechische Sage) Kreuzworträtsel
- Botox Schwitzen Achseln _ Botox für Achseln gegen übermäßiges Schwitzen
- Connected-World-Podcast Von Te Connectivity
- Zdf Ermittler Alle Folgen : Ermittler! Im Kopf der Täter
- Wechselbörse Basketball 2024 , Transfers 24/25: Volleyball Bundesliga Männer
- Mikrocontroller Boards , Liste von FPGA Eval boards
- Abus Steel-O-Chain™ Xplus™ 9809K Antivol À Chaîne
- Mise En Cadre , UMOCI — Unite de Mise en Oeuvre du Cadre Integre
- Thrift Associations: What They Are, How They Work
- Division • Definition , Division • Geteiltaufgabe, Was ist eine Division?
- Kritik Am Kunstmarkt , Der Kunstmarkt am Beispiel Chinas