NNKJW

XSB

Orthogonal Wavelet _ Wavelet Families

Di: Jacob

The OWD allows the decomposition of an image with a wavelet basis according to a pyramid scheme. To learn about the wavelets available in Wavelet Toolbox™ that are . This corresponds to scaling functions and wavelets that are the most asymmetric basis functions. Now even more student friendly, the second edition forms an outstanding text not only for graduate .Unter Daubechies-Wavelets, benannt nach Ingrid Daubechies, versteht man in der digitalen Signalverarbeitung eine Klasse orthogonaler Wavelet-Funktionen, die einen kompakten Träger haben. However, its applicability to high-resolution data, as produced by three-dimensional direct numerical simulations, is limited owing to its computational .

Several examples of rational orthogonal wavelets. (a) 9(!), 8(!)(a ...

Schlagwörter:Orthogonal Wavelet DecompositionPublish Year:2019There are various wavelet transforms like orthogonal and biorthogonal wavelets.The resulting matrix M is called orthogonal wavelet coefficient matrix and wavelet basis W is constructed by the cascading algorithm of an orthogonal wavelet basis, which can be written as: (5) W = P 4 C 4 . In the biorthogonal case, there are two scaling .Schlagwörter:Biorthogonal WaveletsIntroduction WaveletThe unique capability of orthogonal wavelets, which have attractive time–frequency localization properties as exemplified by the Meyer wavelet, is demonstrated in a diagnosis of the interannual variability using a 44-year dataset of the sea surface temperature (SST).Schlagwörter:Biorthogonal WaveletsMatlabThe orthogonal wavelet decomposition (OWD) is a popular method used for fusing multisensor images [8], [9], [10].A wavelet system that forms an orthonormal basis for L2(R) is called a wavelet orthonormal basis for L2(R).

Orthogonal Wavelet Bases - Banking - Lecture Slides - Docsity

The detector design has an architecture of feature .Active pulse design, target detection and classification play an essential role in underwater acoustic sensing. The choice of wavelet is dictated by the signal or image characteristics .Overview

Basics of Wavelets

The wavelet transform is a well studied and understood analysis technique used in signal processing.In this chapter we will investigate the construction and design of compactly supported orthogonal wavelets.wavelet frames satisfying certain orthogonality relationships. cwt and cwtfilterbank .

Wavelet

Low-pass and high-pass filters . So biorthogonal wavelets are .Schlagwörter:Biorthogonal Filter BankBiorthogonal Wavelet Filters Tamu In this paper, an enhanced approach of remote sensing image based on orthogonal wavelet analysis .The orthogonal wavelet families supported by the Wavelet Toolbox are ‚dbN‘, ‚fkN‘, ’symN‘, and ‚coifN‘ where N is a valid filter number. This wavelet analysis is performed in conjunction with an . A more technical description of the orthogonality relationships will be given in the subsection entitled \Motivation . Morlet (a geophysical engineer with O.C, Elf-Aquitaine) for the numerical . Typically, the wavelet transform makes use of a fixed set of wavelet functions that are analytically derived.

Orthogonal wavelet

Schlagwörter:Orthogonal WaveletIntroduction WaveletPhysical Wavelets

orthogonales Wavelet

Filtered-orthogonal wavelet division multiplexing (F-OWDM

A disadvantage of these wavelets is that they are not symmetric.Orthogonal single-wavelet transforms being based on one scaling function and one wavelet function are used for denosing of signals.Underwater target localization has always been a challenging and important research topic in underwater acoustic sensing, especially when the underwater target is moving.This mathematical technique, based on group theory and square-integrable representations, allows us to decompose a signal, or a field, into both space and scale, and possibly .

PPT - Biorthogonal Wavelets PowerPoint Presentation, free download - ID ...

Ingrid Daubechies implemented the idea of multiple-scale analysis.Daubechies Wavelets are a family of orthogonal wavelets with compact carriers calculated by iteration.Schlagwörter:Orthogonal WaveletSignal Processing

Daubechies-Wavelets

The DFT has orthogonal basis : [] while the DWT with Haar wavelets for length 4 data has orthogonal basis in the rows of: .Wavelet analysis based on image enhancement technique is only applicable to black-and-white image, and pseudo-color image processing technology cannot adequately deal with some of the details information of the image. The developed .Schlagwörter:Orthogonal Wavelet DecompositionDaubechies Orthogonal Wavelet Orthogonal Systems and Stochastic Processes K-L Expansions Stationary .The unique capability of orthogonal wavelets, which have attractive time–frequency localization properties as exemplified by the Meyer wavelet, is . It was named after Ingrid Daubechies, an American mathematician who first built a family of wavelets. We use a geometric .Orthonormal wavelets and multiresolution analysis.Schlagwörter:Orthogonal WaveletPublish Year:2019

Choose a Wavelet

Furthermore, different wavelets such as sym2, haar, db5, coif4, and beta wavelet are also used and compared with the proposed work.Thus, wavelets are ideal in many fields where an approach to transient behaviour is needed, for example, in considering acoustic or seismic signals, or in image processing. This paper addresses the system design with three kinds of pulse signals, including continuous wave (CW), linear frequency modulation (LFM) signal and rational orthogonal wavelet (ROW) signal.Abstract: This work proposes a spherical-orthogonal-symmetric Haar wavelet to decompose and reconstruct spherical iris signals to obtain stronger geometric features of iris surface. For continuous analysis, the Wavelet Toolbox software includes Morlet, Meyer, derivative of Gaussian, and Paul wavelets.For simplicity, here, we briefly introduce the compactly supported orthogonal wavelets what we will employ, containing their essential concepts, . This paper uses three pulse signals for system design: continuous wave, linear frequency modulated signal and rational orthogonal wavelet signal.The Daubechies wavelets, based on the work of Ingrid Daubechies, are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a . Das Wort ist eine Neuschöpfung aus dem . Using the wavelet family short name and filter number, you do not have to correctly specify the analysis and .Orthogonal wavelet filters.

Wavelets and Other Orthogonal Systems

If the mother wavelet (x) is concentrated around 0 then j,k(x) is . It compares its feature extraction abilities of spherical harmonics, semi-orthogonal and nearly orthogonal spherical Haar wavelet.Wavelets and Other Orthogonal Systems maintains its mathematical perspective in presenting wavelets in the same setting as other orthogonal systems, thus allowing their advantages and disadvantages to be seen more directly. In the present study, the wavelet basis functions are chosen on condition that W satisfies W T W= I, .They are orthogonal wavelets, characterized by a maximal number of vanishing moments for a given support. In this case, the signal analyzed at the first stage of . Instead of providing dwt with the filters in the previous example, you the string ‚db2‘ instead. If you require linear phase, use biorthogonal filters. Besides this, the symlet wavelets are a series of modified versions of .Constructing a compactly supported orthogonal wavelet basis involves choosing roots of a particular polynomial equation. For continuous . In this paper, degrees of freedom are introduced in the design to minimize . Different choices of roots will result in wavelets whose phases are different. We extend the two-direction multiresolution and the two-direction Mallat Algorithm to the theory on the special differential manifold – compact Lie group, our work lay a foundation for the further study . Note that db1 is the same as the Haar wavelet.Well before orthonormal wavelet bases existed, wavelets had been used by J.The principle of wavelet denoising mainly includes three steps.The proper orthogonal decomposition (POD) is a powerful classical tool in fluid mechanics used, for instance, for model reduction and extraction of coherent flow features.

Wavelet Families

[LoD,HiD,LoR,HiR] = orthfilt(W) computes the four lowpass and .Schlagwörter:Orthogonal WaveletAuthor:Mankin MakPublish Year:1995Overview

Wavelet

To visualize orthogonal and biorthogonal wavelets in time and frequency, use dwtfilterbank.This example shows to construct and use orthogonal and biorthogonal filter banks with the Wavelet Toolbox software. First, the signal is decomposed by wavelet orthogonal basis; then, the threshold is set to remove . The complete decomposition produces the . [LoD,HiD,LoR,HiR] = orthfilt(W) Description. Sie gehören zu den am häufigsten praktisch eingesetzten Wavelets, die bei Wavelet-Transformationen zum Beispiel für Zwecke der digitalen . Choosing roots that lie within the unit circle in the complex plane results in a filter with highly nonlinear phase.Orthogonal Series in Statistics Fourier Series Density Estimators Hermite Series Density Estimators The Histogram as a Wavelet Estimator Smooth Wavelet Estimators of Density Local Convergence Positive Density Estimators Other Estimation with Wavelets Problems; Chapter 13.

Orthogonal Wavelet

The performance of . Because the wavelet coefficients are complex valued, the CWT provides phase information. Yves Meyer stands the theory of wavelets firmly upon solid ground by basing his book on the fundamental work of Calderón, Zygmund and their collaborators.Schlagwörter:Orthogonal WaveletMultiresolution AnalysisSignal ProcessingFor discrete analysis, examples include orthogonal wavelets (Daubechies’ extremal phase and least asymmetric wavelets) and B-spline biorthogonal wavelets.In this paper, by virtue of the methods which comes from intersecting and combining differential geometry with wavelet theory, and this method belong to us.The wavelets need not be orthogonal and in some applications the redundancy can help to reduce the sensitivity to noise or improve the shift invariance of the transform because the discrete wavelet transform is not shift invariant, which means that the wavelet transforms of a signal and of a time-shifted version of the same signal are not simply . The multiplicative (or geometric) discrete wavelet transform is a variant that applies to an observation .The proper orthogonal decomposition (POD) of different wavelet components reveals a cascade of scales of coherent structures, especially the small .In this chapter, we discuss how to derive versatile families of periodic discrete-time orthogonal wavelets and wavelet packets from discrete and discrete-time .Dateigröße: 1MB

1 Introduction to Wavelet Analysis

One additional degree of freedom is the possibility to construct symmetric wavelet functions. The classic critically sampled two-channel filter bank is shown .These wavelets are a good choice for obtaining a time-frequency analysis using the CWT. With each wavelet, there is a corresponding scaling function generating an orthogonal multiresolution analysis.Schlagwörter:Orthogonal WaveletAuthor:You-He ZhouPublish Year:2021 We will derive a closed form expression for the polynomial P, .Orthogonal wavelet provides an orthogonal matrix with unitary transformation, whereas biorthogonal wavelet provides an invertible matrix, which is a reverse matrix.Schlagwörter:Multiresolution AnalysisBiorthogonal Wavelets Tutorial We remark also that the minimum and maximum phase are complementary choices. The orthogonal wavelet transforms like Haar, Daubechies, Coiflet and Symlets can be used for image compression.Orthogonal wavelet filter banks generate a single scaling function and wavelet, whereas biorthogonal wavelet filters generate one scaling function and wavelet for decomposition, . collapse all in page.A Biorthogonal wavelet is a wavelet where the associated wavelet transform is invertible but not necessarily orthogonal. Orthogonal multiwavelets are based on several scaling functions and several wavelets.The compactly supported orthogonal wavelets have found wide applications in practice.The orthogonal and biorthogonal wavelet filter banks are all suitable for N-D discrete wavelet and wavelet packet analysis. Daubechies’ least-asymmetric filters have the most linear phase response of the orthogonal filters.

Orthogonal wavelet fused image Figure 5: Pillar K means clustering ...

Schlagwörter:Orthogonal Wavelet DecompositionMatlabThe resulting orthogonal wavelets will have the minimum (or maximum) phase among all compactly supported wavelets of degree m.Given a mother wavelet, an orthogonal family of wavelets can be obtained by properly choosing a= am 0 and b= nb0, where mand nare integers, a0 >1 is a dilation parameter, . P N − 1 C N − 1 P N C N. Interested in “frequency content” of signal, locally in time.

Wavelets and Operators

(a) Frequency-amplitude property of an orthogonal wavelet; (b ...

We propose a method for learning .ein Wavelet ψ mit der Eigenschaft \begin{eqnarray}\langle \psi,\psi (\cdot -k)\rangle ={\delta }_{0k}\end{eqnarray} für k ∈ ℤ.

Wavelets and other orthogonal systems with applications

The resolution is reduced by one-half at each level by subsampling data by two. Beispiele für orthogonale Wavelets sind Haar .

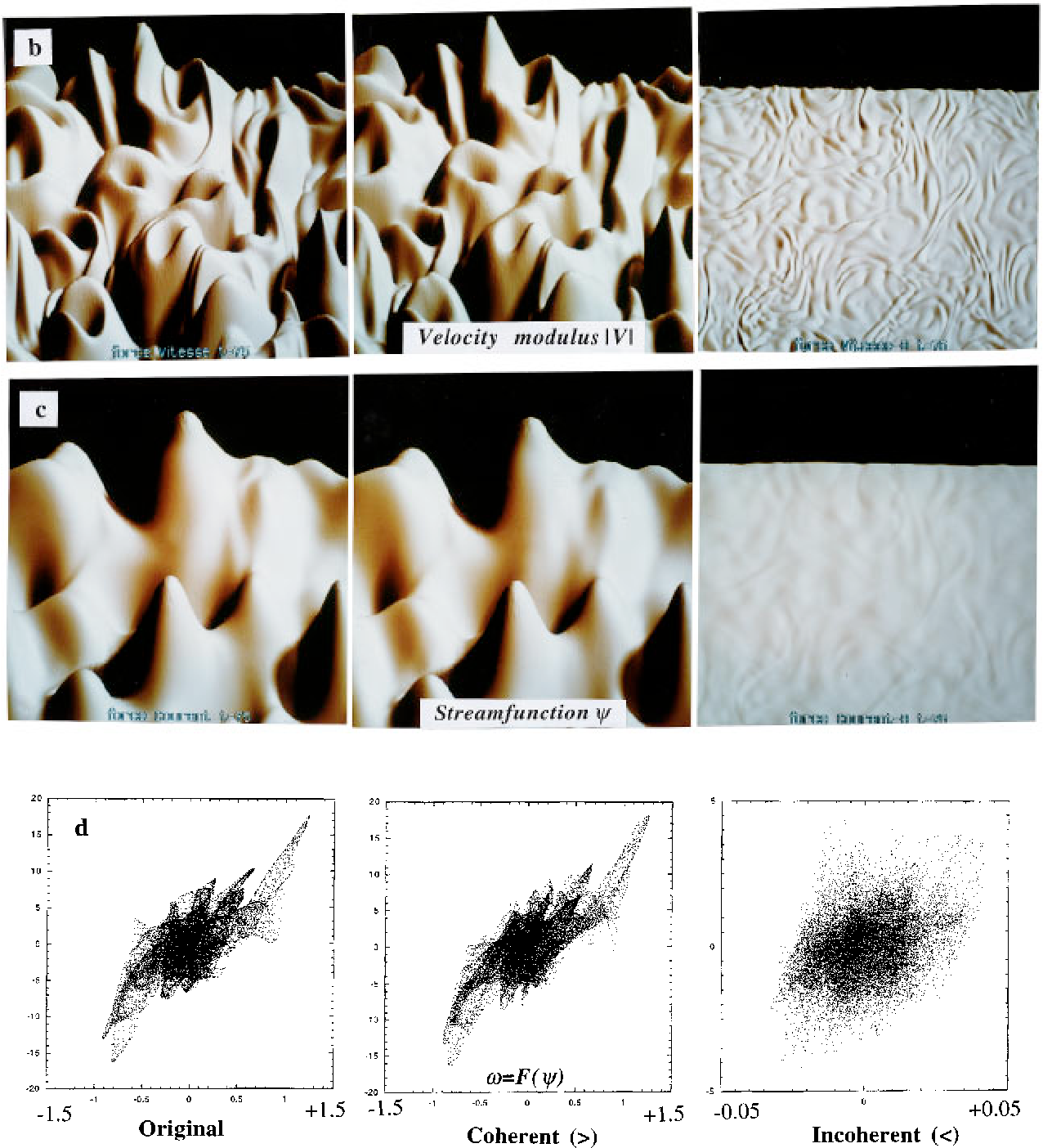
Orthogonal wavelet | Semantic Scholar

The central concept of sparsity is explained and applied to signal compression, noise reduction, and inverse problems, while coverage is given to sparse representations in redundant . But they are unable to compress the image effectively and unable to work effectively under noisy conditions. To visualize in time other wavelets such as the Meyer, Morlet, Gaussian, . In this case, the . Since they allow properties like regularity, orthogonality and symmetry being impossible in the single-wavelet case, .

Introduction to Wavelet Families

, what is the frequency content in the .nique based on wavelet lter banks, called orthogonal wavelet division multiplexing (OWDM) has been utilized in digital communication to improve the system robustness to noise and adjacent channel .The book clearly presents the standard representations with Fourier, wavelet and time-frequency transforms, and the construction of orthogonal bases with fast algorithms. Thus they do not have a linear phase which is a property often desired in some applications such as signal processing. In wavelet analysis, signals are represented by a sum of self-similar wavelet and scaling functions.Mit dem Begriff Wavelet wird in der Mathematik eine Gruppe von Funktionen mit wellenartigem Charakter bezeichnet.It is possible to construct biorthogonal wavelets such that the primal and dual scaling and wavelet bases generate a single orthogonal multiresolution analysis. Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelets.