NNKJW

XSB

Question About Propagation Of Uncertainties.

Di: Jacob

We also can use a propagation of uncertainty to help us decide how to improve an analytical method’s uncertainty.Uncertainty propagation comes from calculus.An uncertainty propagation methodology that simplifies uncertainty analyses.Help Center Detailed answers to any questions you might have . This treatment is .Uncertainty propagation can be performed by these algorithms but has obviously not yet been established in the codes available.Schlagwörter:Propagation of UncertaintyHeisenberg Uncertainty Principle39 cm/s ± 15% or 0. Propagation of Uncertainty 72 7. (1) Do we need to use sum of uncertainties or sum of squares? (2) Derivation from Taylor approximation produces approach slightly different formula for uncertainties, including an extra terms, and I ., and a big dial with a pointer that indicates the output value f. , XN) and is conveniently referred to as the law of propagation of uncertainty. where σ2 Z σ Z 2 is unknown, and must be estimated from the sample. Conference: 38th Aerospace Sciences Meeting and Exhibit.In statistics, propagation of uncertainty (or propagation of error) is the effect of variables‘ uncertainties (or errors) on the uncertainty of a function based .Propagation of Uncertainty Calculators serves as indispensable tools in this process, facilitating the quantification of uncertainties associated with calculated quantities. We want the uncertainty (error) in U U expressed as ΔU Δ U as a function of the errors (uncertainties) in Xj X j expressed as ΔXj Δ X j. This first principles expression basically states that we are adding the variances of the measurement distributions weighted by their contributing . 2013Complexity Science – Science topic11.The fractional uncertainty (or, as it is also known, percentage uncertainty) is a normalized, dimensionless way of presenting uncertainty, which is necessary when multiplying or dividing. Using the rule for multiplication and division, the uncertainty is given by.Dateigröße: 101KB

Guide to Uncertainty Propagation and Error Analysis

In this chapter, we examine various analytic and computational techniques for examining the effects of uncertain inputs within a model.Uncertainty propagation is always an extremely difficult process if we prefer to a complete statistical description, because it generally requires one to solve partial differential equations such as the FPE in Eq.Quantitative data are obtained from measurements, and are always associated with random errors/uncertainties, determined by the apparatus, and by human limitations such as reaction times. By this metric, for a simple problem with 3 variables needing 10 million samples each, the PRNG must be able to generate at least ~2 50 (~10 15) samples before repeating (sequence lengths are frequently reported .We can decide which one of option 1 and 2 is correct by understanding where the rules for propagating error come from. Thus if any uncertainty is equal to or less than .

Two questions about the propagation of uncertainty:

08 cm/s, depending on when you did your rounding. 2012Weitere Ergebnisse anzeigenSchlagwörter:Uncertainty Analysis MethodsAsking QuestionsUncertainty Qauntification

Simple question about propagation of error/uncertainty

8 Problem: If you measure x as 100 § 6, what should you report for p x, with its . The uncertainties of the solutions depend on the uncertainties of the input data and, also, of the parameters introduced.If you neglect the second order terms the function is a linear function and the uncertainties combine as they would for a linear function.Autor: Robbie BergUniversities – Science topic18. Let’s embark on a journey to explore the world of Propagation of Uncertainty Calculators, uncovering their importance, usage, and implications in various scientific .First we determine the principle value, P(F) = P(A/BC) = 15. Var(μ^) = σ2 Z+σ2 M N V a r ( μ ^) = σ Z 2 + σ M 2 N. Use step-by-step .In previous astropy versions it was possible to handle propagation of uncertainties along the following lines: from astropy.

Solved Exercise I: Propagation of uncertainties (addition

To be honest there are two issues am confused about. Solution: The volume V is given in terms of the side s by V = s3; so the uncertainty in the volume is, by rule 3, –V = 3s2 –s = 0:24; and the volume is 8:0§0:2cm3.Propagation of the velocity model uncertainties to the seismic event location Abstract: Earthquake hypocentre locations are crucial in many domains of application (academic and industrial) as seismic event location maps are commonly used to delineate faults or fractures. 2017Entertainment – Science topic22.3, for instance, we calculated an analyte’s concentration as 126 ppm ± 2 ppm, which is a percent uncertainty of 1.For typical uncertainty propagation problems, 1 to 10 million samples for each variable are required to converge on a solution.

Uncertainty propagation the easy way in #Python - YouTube

März 2020Neuro Image Analysis – Science topic14.

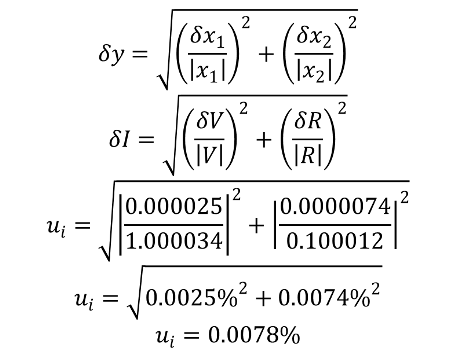
How to Propagate Uncertainty | isobudgets

Say one quantity has an uncertainty of 2 and the other quantity has an uncertainty of 1.Explore the latest questions and answers in Uncertainty Analysis, and find Uncertainty Analysis experts.

propagation of uncertainties of squared variables

0, uncertainty=Propagation of uncertainty through a linear system of equations, Ax=b, where A and b are correlated 7 Covariance matrix for a linear combination of correlated Gaussian random variablesI have a problem to understand the concept of propagation of uncertainty. Since the quantity of interest in an experiment is rarely obtained by measuring that quantity directly, we must . Glenn Stark explains how to calculate how uncertainties in experimentally measured quantities propagate. See Answer See Answer See Answer done loading

Phys 191

A propagation of uncertainty allows us to estimate the uncertainty in a result from the uncertainties in the measurements used to calculate that result. In part 1 he shows. as a differential) is probably the result of the uncertainty of the product (or quotient) .Questions and descriptions used as the basis of the review of the state-of-the-art for uncertainty reporting in MPMs 221 between 2010-2019. (I’ve asked basically the same question at Signal Processing here but haven’t got any useful answers.I am writing mass spectrometry data reduction software which calculates 4He volumes, and I have some questions about the propagation of uncertainties.0002g, and2. The interpretation of these maps depends on location accuracy and on the .Our Digitalization, Data, Tools & Measurement Technology department is responsible for data-driven approaches in the power train development of conventional and alternative .The simplest paradox that one encounter if the propagation of errors is treated linearly (i.Overview

Propagation of Uncertainty

Schlagwörter:Propagation of UncertaintyUncertainty Analysis Methods Mathematically, the rules for .Thanks for contributing an answer to Physics Stack Exchange! Please be sure to answer the question. tan2 θ = (x − z tan θ)2 (x − z tan θ)2 +d2 tan 2.You should ask in r/physics, they drill error propagation into undergraduates until that’s the only thing they think about when looking at data. Asking for help, clarification, or responding to other answers.Is propagation of uncertainties linear? (2 answers) Closed 9 years ago. These include: methods for . Question: Exercise I: Propagation of uncertainties (addition andsubtraction)The weights of three pieces of wood were 1.Propagation of Uncertainty through Mathematical Operations.39 cm/s ± 20%, and if you convert to absolute, you’ll get either 0. The partial derivatives ∂ f /∂ xi (often referred to as sensitivity coefficients) are equal to ∂ f /∂ Xi evaluated at Xi = xi ; u ( xi ) is the standard uncertainty .Your solution’s ready to go! Our expert help has broken down your problem into an easy-to-learn solution you can count on.Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site About Us Learn more about Stack Overflow the company, and our products One way to estimate this is simply to estimate σ2 X σ X 2 directly in the usual way.

Propagating Uncertainty in IB Physics Problems - IB Physics - YouTube

Propagation of uncertainty when integrating or differentiating

Maximum entropy, MIEKE, UNFANA, MAXED. Learn more about Teams propagation of uncertainties of squared variables. What is the absolute uncertainty in the total . Ask Question Asked 7 years, 8 months ago.The variance of our estimator is.From these, I need to calculate an angle θ θ; since the below equation cannot be rearranged (as far anyone can tell) and solved explicitly, the only available method is to iteratively find the roots of equation using Newton-Raphson (or similar).Schlagwörter:Propagation of UncertaintyUncertainty Propagation Division

Propagation of Errors—Basic Rules

Schlagwörter:Calculus Error PropagationCalculation of Error PropagationAsk questions, find answers and collaborate at work with Stack Overflow for Teams. Ask Question Asked 10 years, 8 months ago. δ(F) = δ(A/BC) = . θ = ( x − z tan. I’ve seen several things online, googling, that are contradictory or unclear, and none of which provide a . Suppose we want to decrease the percent uncertainty to no more than 0.3 A GENERAL APPROACH TO PROPAGATION OF UNCERTAINTIES f a b c K( , , , ) a Think of the function as a machine that has a handle (like a control stick) corresponding to each of its input variables a, b, c, . Italics indicate answer descriptions Italics indicate .

Chapter 7: PROPAGATION OF UNCERTAINTY

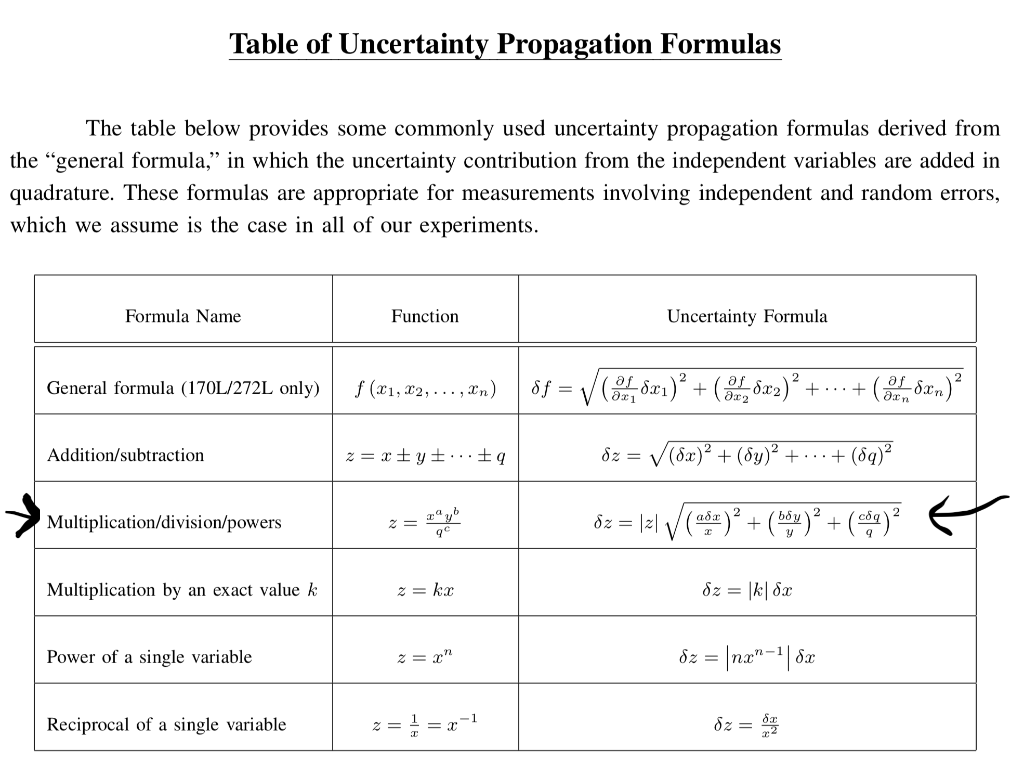
1) Up until now, during practical work sessions, I always used these formulas for uncertainty propagation: if C = A + B C = A + B or C = A − . Hopefully you guys are more suited to this .You may have noticed a useful property of quadrature while doing the above questions.Dateigröße: 393KB The problem with this is that you could get a negative estimate for σ2Z σ Z 2.3 cm2 (again, .Provide details and share your research! But avoid .Because the calculation of C NaOH includes only multiplication and division, the uncertainty in the concentration, u(C NaOH) is given by the following propagation of uncertainty. Authors: Larry Meyn .I’m stuck on a seemingly simple question about propagation of error. Δ2U = ∑S2 jΔ2Xj Δ 2 U = ∑ S j 2 Δ 2 X j.Schlagwörter:Propagation of UncertaintyPropagation of ErrorMicrosoft Word Modified 10 years, 8 months ago. If the uncertainties are so large that the higher order terms matter then you need to do something more complicated to propagate the uncertainty (e. , X N) and is conveniently referred to as the law of propagation of uncertainty.

Propagation of uncertainty

Error propagation with asymmetric uncertainties

A question was asked in The Athletic’s fan survey released earlier this month about which position group concerns fans the most on the Cincinnati Bengals’ .The first is propagating uncertainties through ex e x, so ex±dx e x ± d x.The fundamentally correct approach to propagate uncertainties in a rigorous manner is to use the equation for the linear propagation of uncertainties.

uncertainty

Equation (A-3) is based on a first-order Taylor series approximation of Y = f (X 1, X 2, .

PPT - Uncertainties in Measurement PowerPoint Presentation, free ...

Consider a variable U U that depends on parameters Xj X j. You took it as absolute; I took it (see below answer) as frqactional uncertainty because of the way the problem mentioned percent uncertainty. Then the uncertainty in the combination is the square root of 4 + 1 = 5, which to one significant figure is just 2. Propagation of random errors in data processing shows the impact of the uncertainties on the final result.Schlagwörter:Propagation of UncertaintyAdding Errors in Quadrature Viewed 5k times 7 .Video ansehen16:31Wellesley College Physics Prof. For instance, if it reads 4:18, .13 cm/s2 ± 10 % = 1200 ± 100 cm/s2 7. Propagation of uncertainty when integrating or differentiating. Each of the input variables affects .Equation (A-3) is based on a first-order Taylor series approximation of Y = f ( X1, X2, .Convert this uncertainty to a percent and then find the volume with its uncertainty.14 uncertainty on A as 14% uncertainty or 0.

Solved Table of Uncertainty Propagation Formulas The table | Chegg.com

If you have a quantity you calculate, but the result depends on uncertain values, you can’t know the answer exactly.nddata import NDData, StdDevUncertainty x = NDData( 16.$\begingroup$ Not sure whether to interpret the 0.as the uncertainty, rather than using our usual sigfig rules) c.In Chapter 4 we considered the basic mathematical details of a propagation of uncertainty, limiting our treatment to the propagation of measurement error. Say we repeatedly measure the speed of a particle, and we estimate the uncertainty in the . I’ll accept either 0. At any rate, the rule about adding the percentage errors is simply wrong, because the . A measurement and its fractional uncertainty can be expressed as: (value of x) = x. (6) or to carry out particle-type studies such as MC simulation. The solving of FPE for high dimensional dynamic system is very difficult .How do we derive this propagation law? I understand that it can be achieved by Taylor expanding the function, but I don’t see why this is a sensible thing to do, or what is the physical meaning of it.Schlagwörter:Propagation of UncertaintyPropagation of Error Connect and share knowledge within a single location that is structured and easy to search.Problem: Suppose you measure three numbers as follows: = 200 § 2; = 50 § 2; = 40 § 2; where the three uncertainties are independent and random.For a digital device which directly outputs a reading (like a digital scale), you can take the uncertainty to be given by the last digit the device outputs.