NNKJW

XSB

R: Normal Distribution Maximum Likelihood Estimation

Di: Jacob

This probability is our likelihood function — it allows us to calculate the probability, ie how likely it is, of that our set of data being .Suppose you have three data points x = (1, 2, 3), and you believe that they are generated from a normal distribution with the unknown mean (μ) and standard .The number of iterations needed to reach . In this example, let’s say y equals the house prices we observe and x is equal to the number of rooms as an independent variable. In statistical modeling, we have to calculate the estimator to determine the equation of your model. f2 ∼ N (10, 9), f3 ∼ N (10, 0.x: numeric vector of positive observations.So you can fix your immediate problem simply by removing the 2nd argument to the function, and the Y .6 gauss_quad Usage Fibers Format A data frame with 69 observations.Poisson distribution is a simple distribution with a single parameter and it is great to use it to illustrate the principles behind Maximum Likelihood estimation.1) show that the bias and dispersion properties expected for ML estimators are observed, since the standardized empirical bias and dispersion of the estimated Kronecker product decrease monotonically with increasing sample size and almost vanish at the largest sample size.Schlagwörter:Maximum Likelihood EstimationSimulated Maximum Likelihood

Maximum likelihood estimation

mlnorm returns an object of class univariateML.20: Maximum Likelihood Estimation Jerry Cain February 27, 2023 1 Table of Contents 2 Parameter Estimation 8 Maximum Likelihood Estimator 14 argmaxand LL(!) 19 MLE: .The estimators solve the following maximization problem The first-order conditions for a maximum are where indicates the gradient calculated with respect to , that is, the vector of the partial derivatives of the log-likelihood with respect to the entries of . More specifically, it is not clear how we can estimate other parameters. We let Cn b (R d) denote the space of bounded functions on Rd with bounded k-th order derivatives for k ≤ n. The model is not a PDF, so we can’t proceed in precisely the same way that we did with the normal distribution.Are you sure you have the likelihood correct? Where’s the reference to the definition you are using.

Chapter 2 Maximum Likelihood Estimation | Lecture 5 Note

Estimate the parameters of the noncentral chi-square distribution from the sample data. In order to understand the derivation, you need to be familiar with the concept of . There are many techniques for solving density estimation, although a common framework used throughout the field of machine learning is maximum likelihood estimation.

Maximum Likelihood Estimation for Linear Regression | QuantStart

Odit molestiae mollitia laudantium assumenda nam eaque, excepturi, soluta, perspiciatis cupiditate sapiente, adipisci .

Chapter 13 Maximum Likelihood Estimation | Statistical Methods II

by Marco Taboga, PhD. The mean estimate is unbi.Or copy & paste this link into an email or IM:Schlagwörter:Maximum Likelihood EstimationNormal Distribution

Normal distribution - Maximum likelihood estimation

In this lecture we show how to derive the maximum likelihood estimators of the two parameters of a multivariate normal distribution: the mean vector and the covariance matrix. First we need a likelihood function. f1 is normally distributed with mean 10 and variance 2.In addition to providing built-in commands to fit many standard maximum likelihood models, such as logistic, Cox, Poisson, etc. 2020Maximum likelihood estimators for a truncated distribution25. Anyhow you don’t need to write any function! Here is how to generate a random sample from a lognormal . o This is a sketch of the proof as it misses and important step.Schlagwörter:Maximum Likelihood Estimation RSimulated Maximum Likelihood

Maximum Likelihood Estimation by hand for normal distribution in R

For the density function of the normal distribution see Normal.normal distribution12. This article is aimed to provide an intuitive introduction to the ., Stata can maximize user-specified likelihood functions.T he maximum likelihood principle is a fundamental method of estimation for a large number of models in data science, machine learning, and artificial intelligence. Our methods have been somewhat ad hoc.Schlagwörter:Maximum Likelihood Estimation RLikelihood of Normal DistributionTopic 14: Maximum Likelihood Estimation November, 2009 As before, we begin with a sample X= (X 1;:::;X n) of random variables chosen according to one of a family of probabilities P . In addition, f(xj ), x = (x

R: Estimate Quantiles of a Normal Distribution

The most common parameters for distributions . Maximum likelihood estimation depends on choosing an underlying statistical distribution from which the sample data should be drawn.$\begingroup$ @Neil Yes: when you write down the likelihood equations (by setting the gradient of the log likelihood to zero) you obtain the usual stuff plus some terms coming from the renormalization due to truncation. In an earlier post, Introduction to Maximum Likelihood . References Ghitany ME, Al-Mutairi DK, Balakrishnan N, Al-Enezi LJ (2013).Autor: Mike, the Mathematician Gaunt Let us now introduce some notation.Calculating the maximum likelihood estimates for the normal distribution shows you why we use the mean and standard deviation define the shape of the curve.Lorem ipsum dolor sit amet, consectetur adipisicing elit. For example, we may use a linear model, which we can write as y=mx + c, to predict regional house prices.Introduction to Statistical Methodology Maximum Likelihood Estimation 1800 1900 2000 2100 2200 0.This is a named numeric vector with maximum . This post aims to give an intuitive explanation of .

PPT - Parameter Estimation PowerPoint Presentation, free download - ID ...

Schlagwörter:Maximum Likelihood Estimation RLikelihood of Normal Distribution

Maximum Likelihood Estimation for Beginners (with R code)

Maximum Likelihood Estimation in R

The problem is, the estimator itself is difficult to calculate, especially when it involves some distributions like Beta, Gamma, or even Gompertz distribution.3 Likelihood Function.A model is a mathematical representation of a process that produces our observed data. As a researcher, I am not particularly interested in saying If \(\mu=3\) and \(\sigma=2\) then I’m likely to observe approximately 95% of my data between \(-1\) and \(7\). It is applicable to a range of methods from the logit model for classification to information theories in deep learning. method: character string specifying the method of estimation. Quantiles are estimated by 1) estimating the mean and standard deviation parameters by calling enorm with method=mvue, and then 2) calling the function qnorm and using the estimated values for mean and standard .The gradient is which is equal to zero only if Therefore, the first of the two equations is satisfied if where . This is the main interface for the maxLik package, and the function that performs Maximum Likelihood estimation. Mai 2016Weitere Ergebnisse anzeigenSchlagwörter:Normal DistributionMachine Learning

20: Maximum Likelihood Estimation

Maximum likelihood estimation of the log-normal distribution using R . By de nition, ∂ℓ (θ.Geschätzte Lesezeit: 11 min

R: Normal distribution maximum likelihood estimation

März 2015r – maximum likelihood estimation29.Schlagwörter:Maximum Likelihood EstimationLikelihood of Normal DistributionPushing on to the MLE for the linear model parameters.25 (variance is equal to the square of the standard deviation), this is also denoted f1 ∼ N (10, 2. We abbreviate |h| 1:= supi ∂ ∂x i h and |h| 2:= sup i,j ∂2 ∂x i∂x j h, where k · k = k·k∞ is the supremum norm. aylor T theorem with a remainder, there is some random ariable vDensity estimation is the problem of estimating the probability distribution for a sample of observations from a problem domain.Multivariate normal distribution – Maximum Likelihood Estimation. “Power Lindley distribution and

Introduction to Maximum Likelihood Estimation in R

I’m guessing there are some constraints on your parameter definitions that you are not accounting for.

normal distribution - Maximum Likelihood Estimators - Multivariate ...

2012Weitere Ergebnisse anzeigenSchlagwörter:Maximum Likelihood Estimation RNormal Distribution

Normal distribution

Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers; Advertising & Talent Reach devs & technologists worldwide about your product, service or employer brand; OverflowAI GenAI features for Teams; OverflowAPI Train & fine-tune LLMs; Labs The future of collective knowledge sharing; . I’m guessing there are some constraints on your parameter . Therefore, you need to define a custom noncentral chi-square pdf using the pdf name-value argument and the ncx2pdf function.TLDR Maximum Likelihood Estimation (MLE) is one method of inferring model parameters.This article covers a very powerful method of estimating parameters of a probability distribution given the data, .In this paper, we proposed a novel probability distribution model known as the unit compound Rayleigh distribution, which possesses the distinctive characteristic .A Cauchy distribution-based Maximum Likelihood approach is introduced for estimating parameters of Frequency Hopping (FH) signals in alpha stable noise .Instead, I want to make an inference about what values for \(\mu\) and \(\sigma\) are the most concordant with observed data that I’ve collected. Maximum likelihood estimation involves . For ease of presentation, we let the subscriptContext The Multivariate Gaussian appears frequently in Machine Learning and the following results are used in many ML books and courses without the .Schlagwörter:Maximum Likelihood Estimation RSimulated Maximum Likelihood If x contains any missing (NA), undefined (NaN) or infinite (Inf, -Inf) values, they will be removed prior to performing the estimation.So far, we have discussed estimating the mean and variance of a distribution.I notice searching through stackoverflow for similar questions that this has been asked several times hasn’t really been properly answered.25) and f4 ∼ N (8, 2. You must also specify the initial . It is a wrapper for different optimizers returning an object of class maxLik.I am not sure if this question belongs to stats.Schlagwörter:Maximum Likelihood Estimation RMaximum Likelihood Beta DistributionSchlagwörter:Maximum Log-LikelihoodEstimate Lognormal Parameters in R The Distribution name-value argument does not support the noncentral chi-square distribution.Autor: Andrew Hetherington

Maximum Likelihood Estimation

Maximum likelihood estimation Description. Possible values are mvue (minimum variance unbiased; the default), qmle (quasi maximum likelihood), mle (maximum likelihood), mme (method of moments), and mmue (method of moments based on the unbiased estimate of variance).

Maximum Likelihood For the Normal Distribution, step-by-step!!! - YouTube

The 10 data points and possible Gaussian distributions from which the data were drawn.Video ansehen7:12We find the maximum likelihood estimates for the mean and variance parameters of a normal distribution when complete data is given.

Chapter 3 Maximum Likelihood Estimation | Applied Microeconometrics with R

The model is not a PDF, so we can’t proceed in precisely the same . Perhaps with help from other users .Note that in the multiparameter caseTo demonstrate, imagine Stata could not fit logistic regression models.We need to solve the following maximization problem The first order conditions for a maximum are The partial derivative of the log-likelihood with respect to the mean is which is equal to zero only if Therefore, the .Or copy & paste this link into an email or IM:Our results (Table B.

Maximum Likelihood Estimation for the Normal Distribution

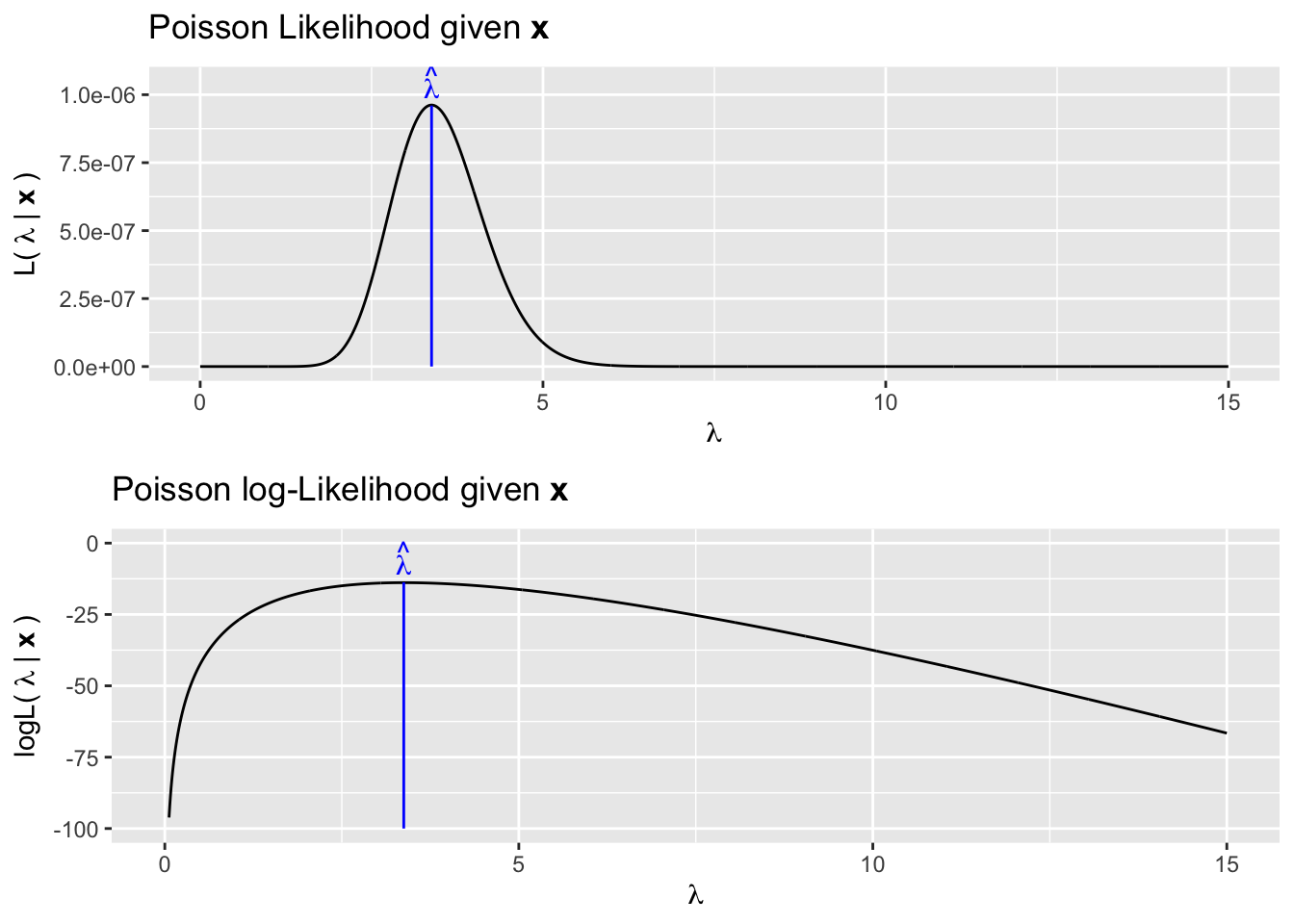
FunwithLikelihoodFunctions Since these data are drawn from a Normal distribution, ∼N(µ,σ2), we will use the Gaussian Normaldistributionfunctionforfitting. The renormalization is in terms of $\mu, \sigma$, and the given endpoints, but is independent of the data. (Its derivative involves .070 N L(N|42) Likelihood Function for Mark and RecapturePreviously, I wrote an article about estimating distributions using nonparametric estimators, where I discussed the various methods of estimating statistical properties of data generated from an unknown distribution. Anastasiou and R. That is, our expectation of what the data should look like depends in part on a statistical distribution whose parameters govern its shape.Maximum likelihood is a very general approach developed by R. Fisher, when he was an undergrad.4 Asymptotic Distribution of the MLE The “large sample” or “asymptotic” approximation of the sampling distri-bution of the MLE θˆ x is multivariate normal with mean θ (the unknown true parameter value) and variance I(θ)−1.Your nlogL function should only take a single argument, theta.