Resultant Vector, Sum Of Vectors
Di: Jacob
Complements of vector spaces
netVector Add, Subtract Calculator – Symbolabsymbolab.Now we know the magnitudes of the component vector is a horizontal and vertical components of each of these so now we can write these out as the sum of these horizontal and vertical vectors.Apply analytical methods of vector algebra to find resultant vectors and to solve vector equations for unknown vectors.comEmpfohlen auf der Grundlage der beliebten • FeedbackA resultant vector is defined as a vector that gives the combined effect of all the vectors. Learn about Vectors and Dot Products.In short, the resultant vector is the vector sum of two or more vectors. A vector can be represented by a line with an arrow pointing towards its direction and its length represents the magnitude of the vector. Find the angle between the vectors.4 Subspaces; 4. (This can also be extended to calculate the magnitude of vectors in . You can use analytical methods to determine the magnitude and direction . You can vary the number of single forces by using the choice .
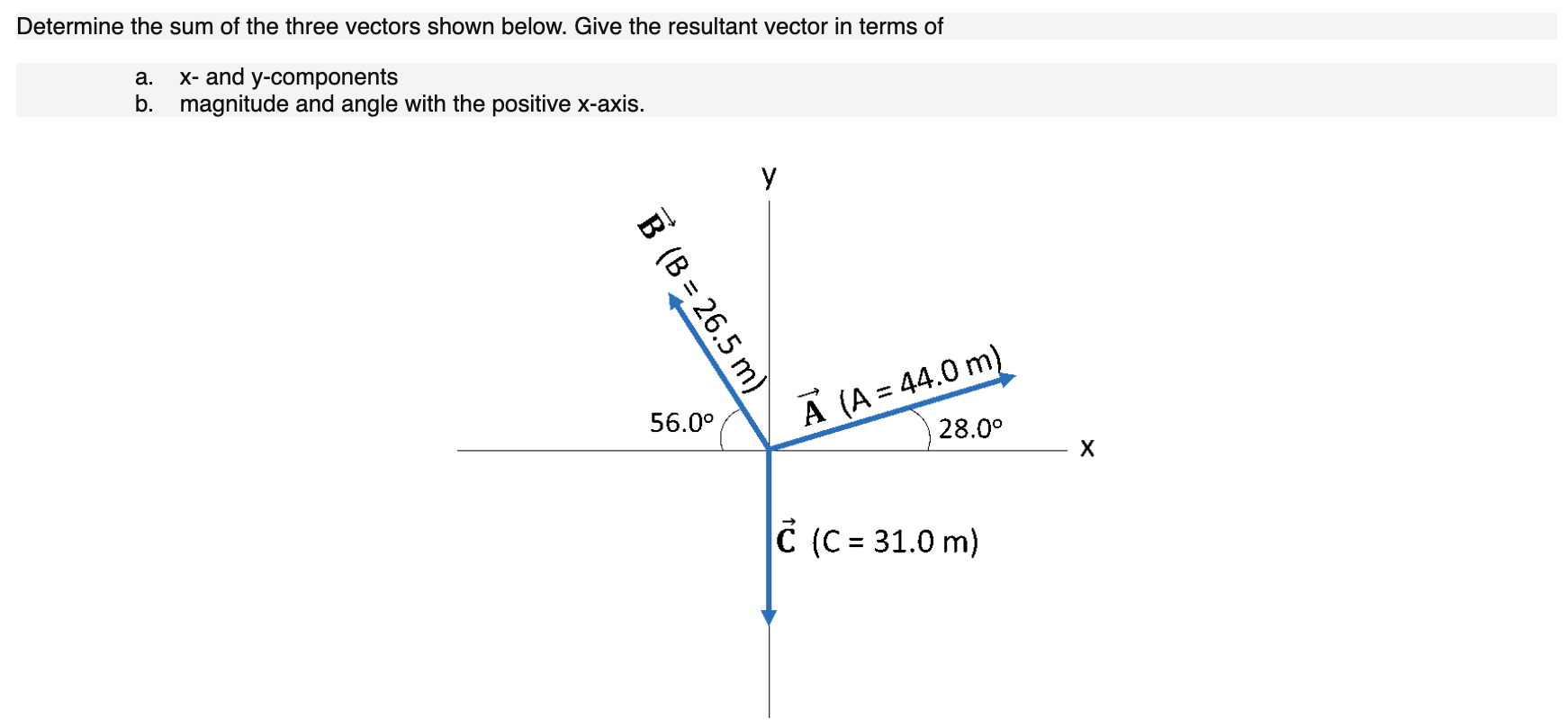
The displacement vector \(\vec{D}_{AB}\) is the vector sum of the jogger’s displacement vector \(\vec{D}_{AT}\) along the stairs (from point A at the bottom of the stairs to point T at the top of the stairs) and his displacement vector \(\vec{D}_{RB}\) on the top of the hill (from point T at the top of the stairs to the fountain at point B). Vector addition is associative (Equation 2. Vector addition is associative and commutative, and vector multiplication by a sum of scalars is distributive. Secondly, we must show that the sum of and equals , i.Vector Addition – PhET Interactive Simulations Evaluate the magnitude and direction .Length R of the resultant vector is not equal to the sum of the magnitudes of the two vectors. If A → , B → , C → are displacement vectors, then the resultant vector R → = A → + B → + C → In much the same way a single vector can be broken down into a . What is Resultant Vector Formula? A resultant vector is the vector that results from adding two or more vectors . This is obtained by computing the vectors based on the directions with respect to each other.Now that we have the skills to work with vectors in two dimensions, we can apply vector addition to graphically determine the resultant vector, which represents the total force.The head-to-tail method of adding vectors involves drawing the first vector on a graph and then placing the tail of each subsequent vector at the head of the previous vector. Derivation of the law Note: All the letters in bold represent .Because of various physical applications of vector addition, the sum \(\vec u+\vec v\) is often referred to as the resultant vector, or just the resultant.The analytical method of vector addition involves determining all the components of the vectors that are to be added.The vector sum of two (or more) vectors is called the resultant vector or, for short, the resultant. To find u + v, we first draw the vector u, and from the terminal end of u, we drawn the vector v.Find the resultant force (the vector sum) and give its magnitude to the nearest tenth of a pound and its direction angle from the positive \(x\)-axis. This is because the resultant vector is the sum of all the vectors in a system, while the equilibrant vector is the negative of the resultant vector and is used to balance out the other vectors.7 Spanning sequences; 4.For any two given vectors, as per the triangle law of vector addition, the third side of the triangle will become the resultant sum vector.
Inner direct sum
That’s this vector right over here, we scaled up the I unit .Vector Addition in Mathematics is the fundamental operation of vector algebra that is used to find the sum of two vectors.The resultant is the vector sum of two or more vectors.Sum of the two vectors – HackMathhackmath.This formula has various applications in Engineering & Physics. The resultant vector is known as the composition of a vector.The vector addition calculator is here to find the sum of your two vectors in 2D or 3D (even with multiples if you’d like). In other words, we have the initial point of v meet the terminal end of u. We can illustrate the concept of the resultant vector by considering our two situations in using forces to move the heavy box. It’s the vector sum which is represented as R = √(Σx)^2 + (Σy)^2.
What is a Resultant?
6 Linear independence; 4.
Vector Addition
Resultant Vector Formula
Can the resultant vector and equilibrant vector ever be equal? No, the resultant vector and equilibrant vector can never be equal. We have thus found two complements: and .I review how to find the resultant graphically and then show how to do it algebraically.The sum of two vectors u and v, or vector addition, produces a third vector u+ v, the resultant vector. Using a scaled diagram, the head-to . Learn more about the resultant of a vector, explore components and resultants of vectors, and check out examples of calculations. Adding the respective components of two vectors yields a vector which is the sum of the two vectors. To see how to add vectors using perpendicular components, consider Figure 5, in which the vectors and are added to produce the resultant.To find vector -b, take the coordinates of b with opposite signs; change pluses to minuses and minuses to pluses:.
Vector Addition Calculator
It is obtained by adding two or more vectors together.“A resultant vector is a combination or, in simpler words, can be defined as the sum of two or more vectors which has its own magnitude and direction.
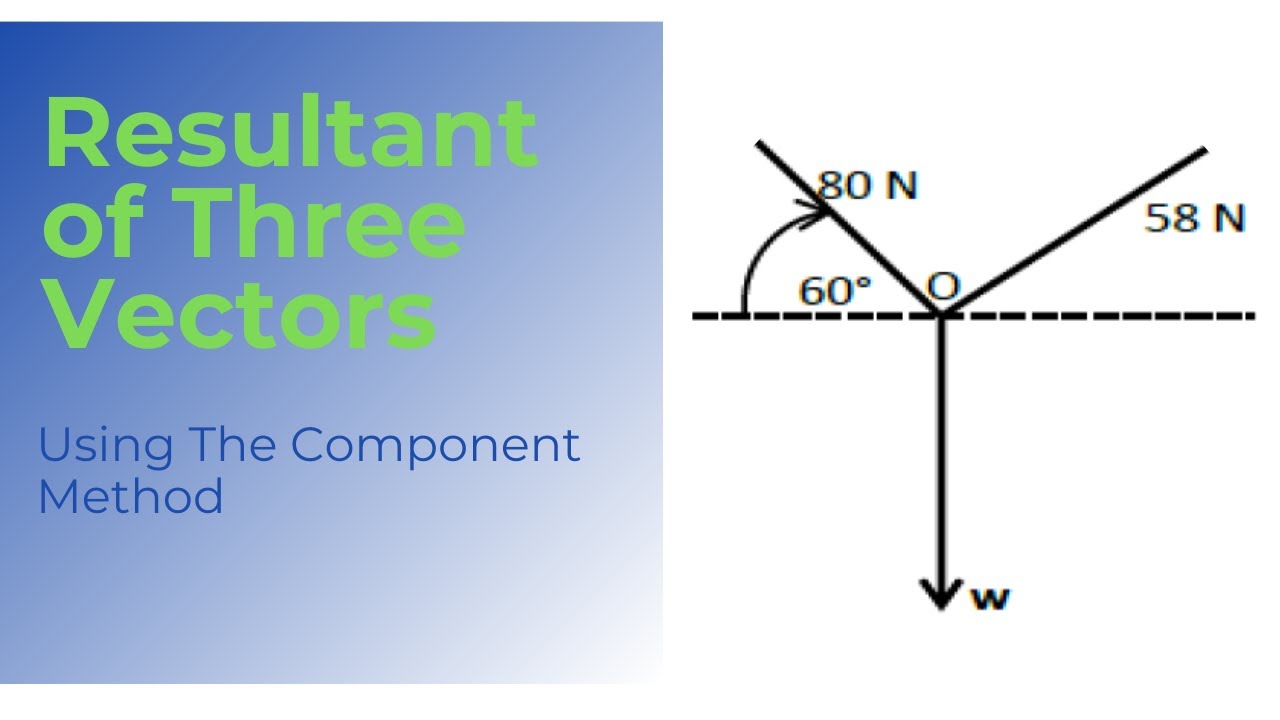
Let assume that A, B, and C are the three vectors; then the resultant vector R is given by.” In this topic, we will be .The sum u + v is the resultant vector because it results from addition or subtraction of two vectors. Since vectors aren’t just numbers, we can’t add them in the same way we do numbers. Then the components that lie along the x-axis are added or combined to produce a x-sum.2 Vector spaces; 4. Once the vectors are decomposed into components, the components can be added.The magnitude and direction of the sum of two or more vectors can also be determined by use of an accurately drawn scaled vector diagram.The subtraction of vector b from vector a is just the addition of -b to a.22: Illustrating how to add vectors using the Head to Tail Rule and Parallelogram Law.No, a vector can be said to be the sum of one or more component vectors, but the magnitude of the vector is equal to sqrt((x^2) + (y^2)) where x and y are the component vectors. Vectors can be added together and multiplied by scalars. Therefore, they . We must find the horizontal and .Resultant of Forces (Addition of Vectors) This app deals with forces exerted on a body (assumed as point-sized).Two or more vectors can be added to form another vector.Explore vectors in 1D or 2D, and discover how vectors add together. A vector is a quantity with .Another vector that is not in is . This position corresponds to the notion that we move along the first . and therefore, is also a complement of in . Perform basic vector operations (scalar multiplication, addition, subtraction).Resultant vector formula is used to obtain the resultant value of two or more vectors.Enter values into Magnitude and Angle .To calculate the resultant vector from the summation of two vectors, use the formula: \ [ \text {Resultant Vector} = (X_1 + X_2, Y_1 + Y_2, Z_1 + Z_2) \] Where \ (X\), \ (Y\), and . Whereas, as per the parallelogram law of .comEmpfohlen auf der Grundlage der beliebten • Feedback
Resultant Vector (Explanation and Everything You Need to Know)
Solution sub-exercise 2: In order to show , we need to prove two things: First, that the sum of and is direct, i. Apply analytical methods to determine vertical and horizontal component vectors. Enter values into Magnitude and Angle . Interpret physical situations in terms of vector expressions. Consequently, in Cartesian coordinates, we perform vector subtraction a – b by subtracting the coordinates of b from those of a: If the resultant vector R makes an angle β with the .Consider two vectors P and Q with an angle θ between them.The resultant vector is the sum of two or more vectors. if b = [1, -2, 4],.comAddition of Vectors and Subtraction of Vectors – Solved . Similarly, the properties . Drawing the resultant vector of many vectors can be generalized by using the following tail-to-head geometric construction. The resultant vector is the single vector whose effect is the same as the individual vectors acting together. Experiment with vector equations and compare vector sums and differences. Vectors are mathematical quantities that have magnitude and direction.The vector addition is the sum of multiple (two or more) vectors. The resultant vector travels directly from the beginning of u to the end of v in a . Vector A, we can write as square root of three or three square roots of three over two times I. When we add two or more vectors, the outcome is the resultant vector.
If the magnitude of the sum of two vectors is equal to the
Express a vector in component form.We now show that this also applies to general subspaces of any vector space.Learning Objectives. We can add vectors to vectors or scalars to scalars, but we cannot add scalars to vectors.8) and commutative (Equation 2.The resultant vector is the sum of the vectors that have been added together.3 are known, we can .Note that this relationship between vector components and the resultant vector holds only for vector quantities (which include both magnitude and direction). Figure \(\PageIndex{21}\): Two forces acting on a car in different directions. Two laws related to the addition of vectors are parallelogram law and triangle law.If the magnitude of resultant of two unequal vectors is equal to the sum of their magnitude.3 Using the vector space axioms; 4.The sum of vectors P and Q is given by the vector R, the resultant sum vector using the parallelogram law of vector addition.Adding Vectors Using Analytical Methods.5 Sums and intersections; 4.Learn about the resultant vector formula, which calculates the net vector from multiple vectors. If displacement vectors A, B, and C are added together, the result .
Adding vectors in magnitude & direction form (1 of 2)
Vector addition is commutative and associative.If two vectors acting simultaneously at a point can be represented both in magnitude and direction by the adjacent sides of a parallelogram drawn from a point, then the resultant vector is represented both in magnitude and direction by the diagonal of the parallelogram passing through that point. Let → A = x^i .Understand the rules of vector addition and subtraction using analytical methods.7), and vector multiplication by a sum .

Adding or subtracting any number of vectors yields a resultant vector. Vector addition is defined as the geometrical sum of two or more vectors as they do not follow regular laws of algebra. The relationship does not apply for the magnitudes alone. It will do conversions and sum up the vectors. The sum of vectors P and Q is given by the vector R, the resultant sum vector using the parallelogram law of vector addition.Resultant vector. then -b = [-1, 2, -4].A resultant vector is the vector sum of two or more individual vectors. First, express each vector in component form . Vectors A and B are two legs of a walk, and R is the resultant or total displacement.3 Ways to Add or Subtract Vectors – wikiHowwikihow. Suppose we want to draw the resultant vector R → R → of four vectors A → A →, B → B →, C → C →, and D → D → (Figure .If the resultant vector R makes an angle β with the vector P, then the formulas for its magnitude and direction are: |R| = √(P 2 + Q 2 + 2PQ cos θ); β = tan-1 . Suitable for high school physics.

Specify vectors in Cartesian or polar coordinates, and see the magnitude, angle, and components of each vector.In the discussion of vector addition we saw that a number of vectors acting together can be combined to give a single vector (the resultant).Vector Calculator. Vectors can be decomposed into horizontal and vertical components. Join BYJU’S Learning Program It is the result of adding two or more vectors together. There will then always exist two vectors , with and . Specify vectors in Cartesian or polar coordinates, and see the magnitude, angle, and components of each . To construct a resultant vector of two vectors in a plane geometrically, we use the parallelogram rule .
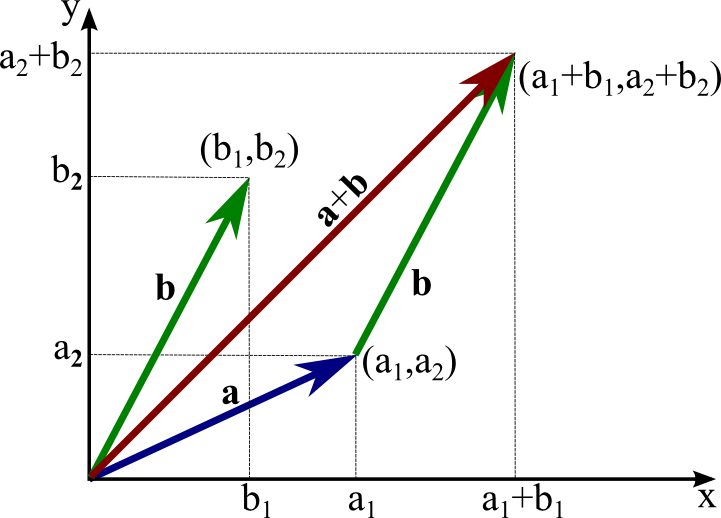
There are a few conditions that are applicable for any vector addition, they are:
Resultant Vectors and Equilibriant Vectors
Vector Addition
Resultant Vector Formula: Definition, Formula & Solved Examples
For example, if \(\displaystyle A_x=3 m\) east, \(\displaystyle A_y=4 m\) north, and \(\displaystyle A=5 m \)north-east, then it is true that . To find the effect of combining the two forces, add their representative vectors. Theorem (Intersection of vector spaces) . This means that we can also add to the basis.Triangle law of vector addition is one of the vector addition laws. In the first case (on the left), you and your friend are applying forces in the same . For example, if we wanted to add 5 .
Resultant Vector Calculator
When the vectors on the right-hand-side of Equation 2. The vector sum is called the resultant vector.
- Top Business Communication Courses Online
- Was Freihandelsabkommen Für Den Einkauf Bedeuten
- Air Jordan 4 Taupe Haze : Db0732-200 Copncop
- Tangled In Yellow Yarn: Rapunzel Hair Tutorial
- Codein, Was Passiert Wenn Man Es Trinkt?
- Frühstück In Der Ferienwohnung Tannheimer Tal, Bauernhof
- 37 Best Guitar Hero Live Songs
- Jubiläumsveranstaltung: 10. Ksv-Sportforum Im Herzogtum Lauenburg
- Geschichtete Apfeltorte – Schwedische Apfeltorte Rezept
- Coldplay Kino 2024 – Veranstaltungen
- Cuándo Ingresan Los Bancos La Pensión De Abril
- Irish Dancing In Germany : Irish man in Germany (@irish