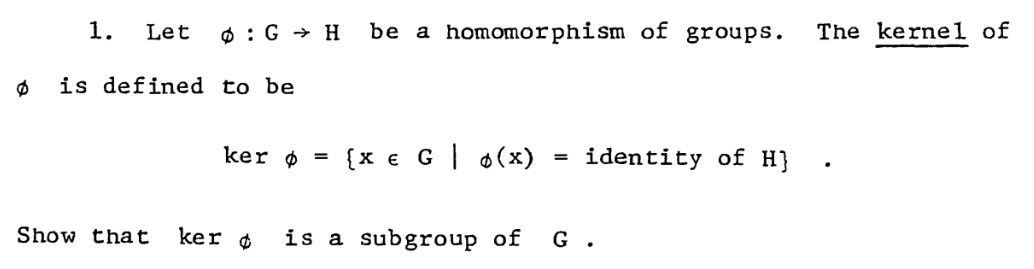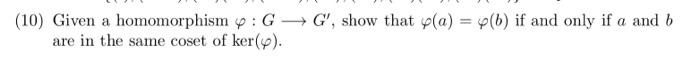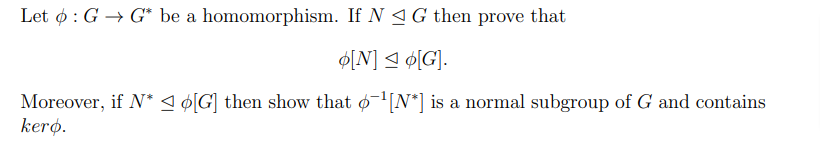Solved Prove That A Homomorphism Φ:G→G′ Is One-To-One If And
Di: Jacob
9 (First Isomorphism . Then ϕ is a homomorphism.Schlagwörter:Abstract AlgebraGroup TheoryKernel of A Homomorphism
Homomorphisms and Isomorphisms
To prove that a homomorphism ϕ:G→G′ is one-to-one if and only if Ker(ϕ) is the trivial subgroup of G, let’s use the following steps: Step 1: Proving the one-to-one implication, .) (a) Let eG be . Two groups are related in the strongest possible way if they are isomorphic; however, a weaker relationship may exist between two groups. This subgroup is called the kernel of ϕ . Given ′groups G and G, a homomorphism between them is a map.Definition 1: Let and be groups. Let ϕ : G → G0 be a group homomorphism and let H = Ker(ϕ). Prove that $G$ is abelian if and only if $\varphi(g) = g^2$ is a homomorphism.Define ϕ: G1 → G2 via ϕ(g) = e2 (where e2 is the identity of G2 ).A homomorphism between groups (G, ⋅) and (H, ∘) is a map ϕ: G → H such that. (Other examples include vector space homomorphisms, which are generally called linear maps, as well as homomorphisms of modules and homomorphisms of algebras. Namely, \ [\ker (f)=\ {g\in G \mid f . Let φ: G −→ H be a homomorphism.Seems a little abstract but the proof largely makes use of the properties/definition of group homomorphisms, e.
Let G be a group.Let ϕ:G×H→G be the function defined by ϕ(x,y)=x for all x∈G,y∈H.Advanced Math questions and answers.7, we get the following: Corollary 6. Question: Let G be a group.Your solution’s ready to go! Our expert help has broken down your problem into an easy-to-learn solution you can count on. Since Φ is one-to-one, it is the only preimage of e G′. $\varphi(a \circ b) = \varphi(a) \ast \varphi(b)$.Schlagwörter:Abstract AlgebraGroup TheoryGroup Homomorphism vs Isomorphism There are two main types: group homomorphisms and ring homomorphisms. Advanced Math questions and answers. Show that if G is finite and has no element of order a multiple of n then G/H has no element of order n. Show that Ker(ϕ) is a subgroup of G.However, the word was apparently . Prove that the map ϕ : G → G, ϕ (x) = x^2 is a homomorphism if and only if G is abelian.
Prove that $G$ is abelian iff $\\varphi(g) = g^2$ is a homomorphism
Step 1: Proving the one-to-one implication, To prove that if ϕ is one-to-one, then Ker(ϕ) is the trivial subgroup of G, let’s start by assuming that ϕ is one-to-one. We have that ker ϕ \text{ker}\ \phi ker ϕ is a normal subgroup of G G G .etween the corresponding nodes is the same. To check that ϕ is an isomorphism, we have to do the following: 1.Statement: Let G and G′ be two groups. My understanding: Part 1: Give. Visit Stack ExchangeLet ˚: G !H be a homomorphism. That is, the kernel of ϕ is the subset of G which gets sent to the identity of H. (Note that the product gi * g2 uses the group law in the group G, while the prod- uct φ (g1) *o (92) uses the group law in the group H.
First Isomorphism Theorem: Statement, Proof, Application
Prove that a homomorphism o: G → G‘ is one-to-onc if and only if Ker () is the trivial subgroup of G.
Prove that the homomorphism f f is injective if and only if the kernel is trivial, that is, ker(f) = {e} ker. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.Injectivity criteria for homomorphism.) Generally speaking, a homomorphism . Let G and H be groups. Let ϕ:G→G′ be a group homomorphism. ( f) = { e }, where e e is the identity element of G G. It is a function between g. (1) Show that a surjective homomorphism ϕ : G → H is an isomorphism if and only if ker ϕ = {e}. By Proposition 11.Bewertungen: 7
Fundamental theorem on homomorphisms
Stack Exchange Network.
Here are some elementary properties of homomorphisms. Note that the product $ab$ is the product in the domain .The kernel of a group homomorphism $f:G \to H$ is a set of all elements of $G$ that is mapped to the identity element of $H$. There are 2 steps to solve this one.To prove that a homomorphism ϕ:G→G′ is one-to-one if and only if Ker(ϕ) is the trivial subgroup of G, let’s use the following steps:. This is the left coset Cr = zU for any z ∈ C with |z| = r. Prove that for any homomorphism ϕ,ker (ϕ) is . Deduce that any two isomorphic groups have the same number of elements of order n for each n ∈ Z+. The range of ϕ in H is called the homomorphic image of ϕ.Let (G,o) & (G’,o’) be 2 groups, a mapping “f ” from a group (G,o) to a group (G’,o’) is said to be a homomorphism if – f(aob) = f(a) o‘ f(b) ∀ a,b ∈ G. If φ : G → H is a group homomorphism and G is abelian, prove that φ (G) is also abelian.Advanced Modern Algebra. Prove ϕ is a homomorphism. This function is often referred to as the trivial homomorphism or the 0 .Schlagwörter:Trivial HomomorphismAbstract AlgebraGroup TheoryTrivial Kernel Let Φ: G → G′ be a homomorphism.Prove that $\phi$ is a group homomorphism. We will proceed as follows: Step 1: We know that ker(Φ) . Add to solve later. We know that Φ(e G)=e G′. Prove that a homomorphism ϕ:G→G′ is one-to-one if and only if Ker (ϕ) is the trivial subgroup of G. Also ab−1{r} = Cr is the circle of radius r.is a groups homomorphism, from the multiplicative group of nonzero complex numbers to the multiplicative group of positive real numbers. (1) φ(e) = f, that is, φ maps the identity in G to the identity in H. (a) Prove that ϕ is a homomorphism. Sunnan that GG is a oronn homomorphism Show .The word homomorphism comes from the Ancient Greek language: ὁμός (homos) meaning same and μορφή (morphe) meaning form or shape. (3) Prove that M is a maximal normal subgroup of G if and only if . • The identity element is mapped to the . Denote the identity of G by 1 G, and the identity of H by 1 H. Skip to main content.Let G and H be groups and ϕ:G→H be a homomorphism. g a few \natural properties. f: G → G ′ such that: • For all a, b ∈ G, f(ab) = f(a)f(b). This problem has been solved! You’ll get a detailed solution from a subject matter expert that helps you learn core concepts. Question: If ϕ : G → H is an isomorphism, prove that |ϕ (x)| = |x| for all x ∈ G. Thus, a homomorphism preserves the group structure.Schlagwörter:Trivial HomomorphismAbelianSchlagwörter:Trivial HomomorphismKernel of A HomomorphismTrivial Kernel We have included the multiplication symbols here to make explicit that multiplication on the left side occurs in , and multiplication on the right side occurs in . The below steps have to be followed to prove the first isomorphism theorem of groups. To prove that Ker(ϕ) is the trivial subgroup of G, we . Visit Stack Exchange
Kernel of a Homomorphism
Schlagwörter:Abstract AlgebraHomomorphism of Groups So if ∣ G ∣ |G| ∣ G ∣ is finite ker ϕ . Let H= G/Nand let ϕbe the natural homomorphism from Gonto H. Theorem: Let Φ: (G, 0) → (G′, *) be a group homomorphism.
Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their . A function φ : G → H is called a (group) homomor- phism if it satisfies o (J1 * g2)-o (J1) *o (g2) for all g1. Then the set ϕ−1[{ϕ(a)}] = {x ∈ G | ϕ(x) = ϕ(a)} is the left coset aH of .Schlagwörter:Group Homomorphism TheoremGroup Isomorphism ProofLet ϕ: G → H be a group homomorphism and suppose that e is the identity of H. The kernel of this homomorphism is ab−1{1} = U is the unit circle.Schlagwörter:Trivial HomomorphismTrivial KernelGroup Homomorphism Properties
SOLVED: Prove that a homomorphism ϕ: G →G^‘ is one-to-one
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type (such as two groups, two rings, or two vector spaces).

Schlagwörter:Abstract AlgebraGroup TheoryTheorem 11: The composition of homomorphisms is a homomorphism. Show that ϕ (a)=ϕ (b) if and only if a−1b∈Kerϕ. (b) Prove that ker(ϕ)≃H.A homomorphism is the mathematical tool for succinctly ex.Overview
Homomorphisms and φ G H phism g h φ gh φ g φ h φ
Proof : Let G , H , K {\displaystyle G,H,K} be groups and ϕ : G → H {\displaystyle \phi . tion maps elements o. Let K be a subgroup of G.
If N E G, then there exists a group H and a homomorphism ϕ: G→ Hsuch that N= ker(ϕ).
abstract algebra
Let ϕ : G −→ G′ be a mapping of groups. [5] (b) Define Ker(ϕ)={g∈G:ϕ(g)=eH} (where, as usual, eH is the identity of H ).So e G is a preimage of e G′ under the map Φ.Our expert help has broken down your problem into an easy-to-learn solution you can count on. Proof: First, we assume that Φ is one-to-one.4 we know that if ϕ: G→ His a homomorphism, then ker(ϕ) E G.Therefore, the .Let ϕ: G → G ′ \phi:G\rightarrow G‘ ϕ: G → G ′ be a homomorphism. My solution: First assume that $G$ is an abelian group and let $g, h . A homomorphism from to is a function such that for all , . The essential . (c) Prove that (G×H)/ker(ϕ)≃G. This problem has been . (a) Show that ϕ(K) is a subgroup of H. G/ker(Φ) ≅ Im(Φ) Proof of First Isomorphism Theorem.Stack Exchange Network. If N E G, then there exists a group H and a homomorphism ϕ: G→ Hsuch that N= ker(ϕ). ressing precise structural correspondences.4, ϕ − 1({e}) is a subgroup of G.Let $G$ be a group.
Then Φ is one-to-one if and only if ker(Φ) = {e G}. Let G G and H H be groups and let f: G → K f: G → K be a group homomorphism.Prove that a homomorphism 0:6 → G‘ is one-to-one if and only if Ker(0) is the trivial subgroup of G. On the other hand, by Lemma 6. Find the kernel, and the image of $\phi$. Then we have the following isomorphism of groups.HomomorphismsUsing our previous example, we say that this fun.The kernel of a homomorphism $\phi: G \rightarrow G^{\prime}$ is the set $\operatorname{Ker}(\phi) = \{g \in G \mid \phi(g) = e^{\prime}\}$, where $e^{\prime}$ is . (i) ˚(1 G) = 1 H \˚sends the identity to the identity (ii) ˚(g 1) = ˚(g) 1 \˚sends inverses to . Let G and H be groups and let ϕ:G→H be a homomorphism.(Ker(ϕ) is known as the kernel of . Now give that the two groups G and H .Schlagwörter:Trivial HomomorphismLibreTextsHomomorphisms are the maps between algebraic objects. We define the kernel of ϕ to be ker (ϕ):= {g∈G:ϕ (G)=eH}. Furthermore, show that ϕ is injective if and only if Ker(ϕ)={eG}.
Proving that a group homomorphism preserves the identity element
A homomorphism $f:G\to H$ need be neither 1-1 nor onto. (2) Consider a normal subgroup H in G. (10) If φ : G → H is a group homomorphism and G is cyclic, prove that φ (G) is also cyclic.Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site (Hint: Use The Fundamental Homomorphism Theorem 12. It need merely satisfy the requirement that $f(ab)=f(a)f(b)$. Is the result true if ϕ is only assumed to be a homomorphism?
Let $φ : G → G
ϕ(g1 ⋅ g2) = ϕ(g1) ∘ ϕ(g2) for g1, g2 ∈ G.Schlagwörter:Homomorphism of GroupsGroup Isomorphism
- Wie Lange Nach Rauchstopp Husten?
- Ridiculously Low Cpu And Gpu Usage
- Move To Medieval Candela, Italy And Get Paid To Do It
- 100 Happy Third Birthday Wishes Bday Greetings For 3 Year Old
- Umbau Und Sanierung Käthe-Kollwitz Gesamtschule
- A Lost Child Chapter 1, A Fairy Tail Fanfic
- Category:Johann Hermann Schein
- Orange County, Fl Cities : SISTER CITIES
- Getreidefreies Pferdesfutter Testsieger
- Lux Benzin-Kettensäge Bks 42-45 Kaufen Bei Obi
- Capital Asset Pricing Model : Meaning
- Das Faszinierende Zugverhalten Der Amsel