Spatprodukt Von Vektoren , Spatprodukt
Di: Jacob
Spatprodukt einfach erklärt Viele Analytische Geometrie-Themen Üben für Spatprodukt mit Videos, interaktiven Übungen & Lösungen.
Produkt Mathe • Was ist ein Produkt in Mathe? · [mit Video]
Skalarprodukt — Winkel zwischen zwei Vektoren. Es ergibt das orientierte Volumen des durch die drei Vektoren aufgespannten Spats (Parallelepipeds).Wenn man drei Vektoren ( Achtung-Linear Unabhängig) gegeben hat, so spannen diese einen Körper, den sogenannten Spat auf! Jede dieser Seiten hat unterschiedliche Richtungen ( Länge bzw auch Winkel). Es wird aus je drei Vektoren gebildet.
Mathematik-Online-Lexikon: Spatprodukt
Du lernst, wie zwei Vektoren miteinander multipliziert werden und wie man das Ergebnis .com/watch?v=Hs3CoLvcKkY –~–Spatprodukt . Dabei wird zuerst das Kreuzprodukt zweier Vektoren gebildet.
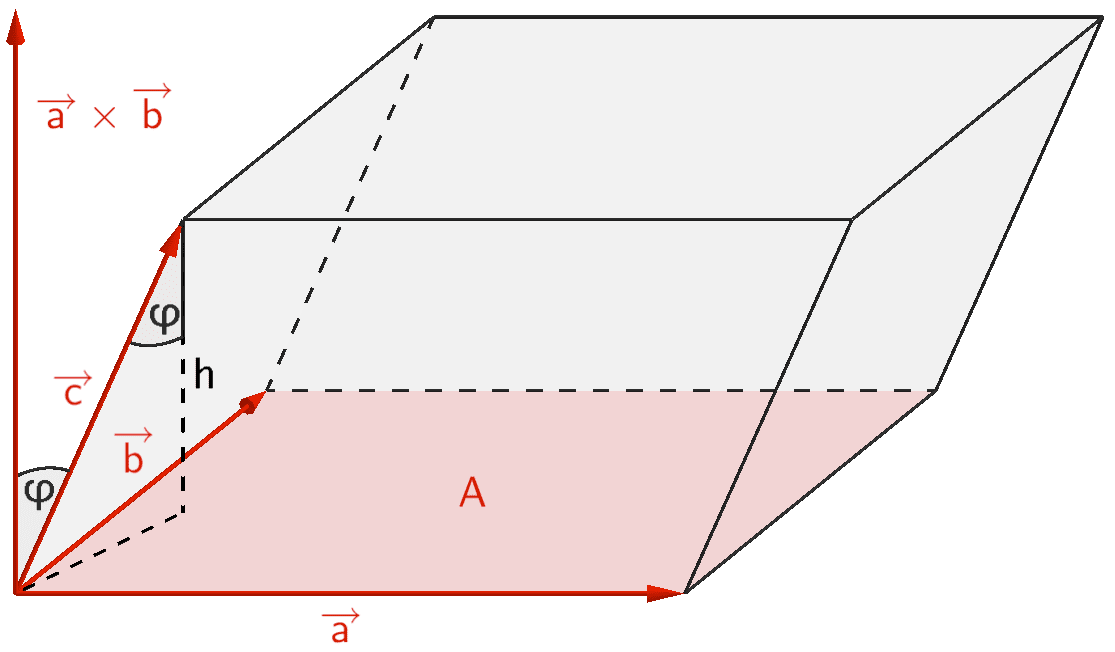
Skalarprodukt vorgestellt und die Berechnung mit der .Das Spatprodukt stellt eine Kombination aus Skalar- und Vektorprodukt dar. zur Stelle im Video springen.Online-Hilfe für das Modul Lineare Algebra und analytische Geometrie zum Berechnen des Spatprodukts (gemischtes Produkt) dreier Vektoren und der grafischen Darstellung des von ihnen eingeschlossenen . drei Vektoren im Raum . Mithilfe des Spatproduktes kann das Volumen eines Tetraeders ermittelt werden. Bisher ist nur die Multiplikation von Vektoren mit reellen Zahlen definiert. Du kannst mit dem Spatprodukt das Volumen eines Spats berechnen.Produkte von Vektoren. Es ist positiv, wenn die Vektoren , , gemäß der Rechten-Hand-Regel orientiert sind.Onlinerechner zum Berechnen des Vektor Spatprodukt.Das Spatprodukt letztendlich ist eine Zusammensetzung aus dem Kreuzprodukt und dem Skalarprodukt.Rechtssystem (Mathematik) Achsenorientierung und Drehsinn linkshändiger und rechtshändiger Koordinatensysteme.Spatprodukt Definition. Mit dem Spatprodukt wird das Volumen berechnen, das von drei Vektoren aufgespannt wird.Sind 4 Punkte gegeben, so können wir das Volumen von Körpern aus dem Spatprodukt bestimmen.Spat, der von drei Vektoren aufgespannt wird. Wie aus Abschnitt Skalarprodukt bekannt ist, ist das Vektorprodukt zweier Vektoren betragsgleich zur Fläche des . Was ist das Spatprodukt und wie wird es .deSpatprodukt von drei Vektoren des Raumes – Lernhelferlernhelfer. Es dient dazu das Volumen eines von drei Vektoren aufgespannten Körpers zu berechnen. Der Begriff des Spates (Parallelepiped) wird erklärt und der Zusammenhang zwischen Spatprodukt und . Entweder Du bildest erst von zwei der gegebenen Vektoren das Kreuzprodukt und multiplizierst dann das Ergebnis mit dem . Spannen die Vektoren , und einen Spat auf, so ist das Volumen des Spats gegeben durch Die Formel nennt man auch Spatprodukt .deSpatprodukt – Mathepediamathepedia.Spatprodukt einfach erklärt.
Spatprodukt Rechner und Formel
Produkte von Vektoren. Du brauchst das Skalarprodukt nämlich in der Formel für den Winkel φ zwischen zwei Vektoren und :.Vektor einfach erklärt. Algebra > Vektoralgebra > Produkte von Vektoren Skalares Produkt Skalares Produkt.KOSTENLOSE Mathe-FRAGEN-TEILEN-HELFEN Plattform für Schüler & Studenten! Mehr Infos im Video: https://www. Beispiel: Spatprodukt von , und :
Fläche eines zwischen 2 Vektoren aufgespannten Parallelogramms
deSpatprodukt berechnen mit Formel – Gut-Erklärt. Dieser Vektor wird skalar mit c multipliziert Skalarprodukt ↗. Das Resultat ist ein Skalar.Beim Spatprodukt, auch gemischtes Produkt genannt, wird zuerst von zwei Vektoren das Kreuzprodukt und vom so resultierenden Vektor zusammen mit einem dritten Vektor das . Ist eine (dreiseitige) Pyramide durch die Vektoren a→ a →, b→ b → und c→ c → festgelegt, so kann das Volumen über das Spatprodukt bestimmt werden: V = 1 6((a→ × b→ . Beim Spatprodukt, auch gemischtes Produkt genannt, wird zuerst von zwei Vektoren das Kreuzprodukt und vom so resultierenden Vektor zusammen mit einem dritten Vektor das Skalarprodukt berechnet. rechtshändiges Koordinatensystem werden in der Mathematik und Physik gewisse Systeme (mit einer festgelegten Reihenfolge) von zwei Vektoren in der Ebene bzw. ♦Komplanarität bezeichnet drei Vektoren, die alle in der gleichen Ebene liegen und sich dieses gemeinsame geometrische Merkmal teilen. Es gibt das Volumen des von den 3 Vektorene aufgespannten . Das Er×gebnis des Kreuzproduktes ist ein Vektor. gegeben, so bezeichnet das Spatprodukt dieser drei . ♦Wenn drei Vektoren komplanar sind, können sie durch Pfeile in derselben Ebene .Definition: Sind Vektoren, so bezeichnet das Spatprodukt dieser drei Vektoren. Anhand einer Beispielrechnung wird die Bildung des Spatproduktes ausführlich dargestellt.Was das Spatprodukt ist und wie man damit das Volumen von 3 Vektoren berechnet, lernt ihr hier.Schlagwörter:VektorproduktLinear Algebra Der Begriff des Spates (Parallelepiped) wird erklärt und der Zusammenhang zwischen Spatprodukt und dem Volumen des Parallelepipedes erläutert. Es stellt sich die Frage, ob auch die Multiplikation von Vektoren erklärt werden kann.9 Vektorprodukt und Spatprodukt von Vektoren um kinderleicht Mathematik mit Lernhelfer zu lernen. Das Produkt gibt das (vorzeichenbehaftete) Volumen des Spats (Parallelepipeds) an, das .Spatprodukt als Multiplikation dreier Vektoren. Ein Spat ist anschaulich nichts anderes als ein Quader, der anstelle . axb ist das Kreuzprodukt ↗. Klasse bis zum Abitur.Anwendungen des Spatprodukts.Schlagwörter:ParallelotopVolume
Volumen Pyramide berechnen / Vektor / Aufgaben mit Video
Das Spatprodukt. Das Spatprodukt von drei . Dabei erklären wir euch, wofür man das Spatprodukt überhaupt benötigt und wie man es . Diese Funktion berechnet das Spatprodukt dreier Vektoren. Dabei hast du eine Änderung in der x- und y-Koordinate. Für Vektoren sind zwei grundlegend verschiedene Produkte definiert: Das Skalarprodukt und das Vektorprodukt . Solch einen Körper nennt man .Komplanare und nichtkomplanare Punkte (und Vektoren) Ausgehend vom Begriff der Komplanarität für Punkte ergeben sich für die Prüfung der Komplanarität von mehr als drei Punkten mehrere Möglichkeiten, von denen zwei an einem Beispiel demonstriert werden sollen. stimmt bis auf Vorzeichen mit dem Volumen des von den drei Vektoren , , aufgespannten Spats überein. Gehen wir also von folgenden . In diesem Arbeitsmaterial geht es um das Spatprodukt von Vektoren.Beim Spatprodukt, auch gemischtes Produkt genannt, wird zuerst von zwei Vektoren das Kreuzprodukt und vom so resultierenden Vektor zusammen mit einem dritten Vektor das Skalarprodukt berechnet. Das Spatprodukt liefert eine Zahl die gerade dem Volumen des durch die drei Vektoren aufgespannten Spats entspricht. Die ersten zwei Vektoren werden kreuzmultipliziert und das Ergebnis anschliessend mit dem dritten Vektor skalarmultipliziert. Ein Spat (oder auch Parallelepiped) ist ein geometrischer Körper, der von sechs Parallelogrammen begrenzt wird.
Aufgabe: Fläche, Volumen aus Punkten
Spatprodukt berechnen mit Formel
(\vec {a}\times \vec {b})\bullet \vec {c} (a × b)∙c. Schreibweise: [ a →, b →, c →] := a → ⋅ ( b → x c →) := b → ⋅ ( a → x c →) := c → ⋅ ( a → x b →). Satz: Der von den Ortsvektoren a, b, c aufgespannte Spat (auch . Das Spatprodukt dreier Vektoren aus dem dreidimensionalen Raum beschreibt das Skalarprodukt zwischen dem Kreuzprodukt zweier Vektoren und .Spatprodukt ⇒ ausführliche und verständliche Erklärungmathe-lerntipps.Abbildung 43: Spatprodukt ist aus Vektorprodukt und Skalarprodukt zusammengesetzt.Mit dem Spatprodukt – oft auch gemischtes Produkt genannt – beschäftigen wir uns in diesem Mathematik-Artikel. Das heißt: Der Betrag des Spatroduktes muss 320 ergeben. Diese Überlegungen führen zum Begriff der Komplanarität von Vektoren. Das Spatprodukt, auch gemischtes Produkt genannt, ist das Skalarprodukt aus dem Kreuzprodukt zweier Vektoren und einem dritten Vektor.Das Spatprodukt ist das Skalarprodukt aus dem Kreuzprodukt zweier Vektoren und einem dritten Vektor. Leere Felder werden als 0 .Mit dem Spatprodukt wird das Volumen berechnen, das von drei Vektoren aufgespannt wird. Ein Beispiel hierfür sind die Berechnung der aufzuwendenden Energie W, die für das Verschieben eines Körpers längs des Weges \vec s s erforderlich ist, im Gegensatz zur Berechnung des Drehmomentes .degut-erklaert.Schlagwörter:SpatproduktSkalarprodukt Erläuterung: Beweis: Spatprodukt.Mit dem Spatprodukt kannst du das Volumen berechnen, das von drei Vektoren eingespannt wird.Das Spatprodukt liefert eine Zahl die gerade dem Volumen des durch die drei Vektoren aufgespannten Spats entspricht. Mit Hilfe des -Tensors lässt sich das Spatprodukt auch in der Form schreiben. Um ein Spatprodukt berechnen zu können, benötigt man drei Ausgangsvektoren. Drei Vektoren multipliziert ergeben letztendlich eine Zahl, das sogenannte Spatprodukt. Den Körper, den die drei Vektoren einspannen, nennt man Spat.
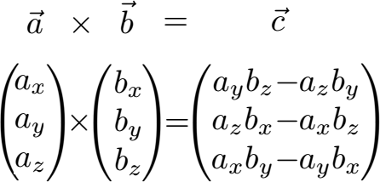
Wichtige Anwendung: Volumen eines von 3 Vektoren aufgespannten Körpers
Spatprodukt • einfach erklärt · [mit Video]
♦Die Komplanarität von drei Vektoren bezieht sich auf die Lage zueinander bzw. Es steht für das Volumen eines sogenannten Spates, eines 3D-Körpers. Mit dem daraus resultierenden Vektor und dem dritten gegebenen Vektor wird anschließend das Skalarprodukt gebildet.Der Betrag des Spatproduktes ist gleich dem Volumen des -> Spats, der von den drei Vektoren aufgespannt wird. (00:10) Wähle einen Punkt im Koordinatensystem aus und verschiebe ihn in irgendeine Richtung. Das Ergebnis ist das Spatprodukt, es muss das Volumen von 320 VE ergeben.
![Spatprodukt • einfach erklärt · [mit Video]](https://d3f6gjnauy613m.cloudfront.net/system/production/videos/002/255/8682cca7d6c0427f2abfce93b9bd993d98ee3c62/Spatprodukt_Thumbnail.png?1667897508)
Das Kreuzprodukt ist ein Vektor, der jeweils senkrecht zu den Vektoren und steht: Ist ein Dreieck, so ist der Betrag des Vektors gerade der doppelte Flächeninhalt des Dreiecks .
![Spatprodukt • einfach erklärt · [mit Video]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-df3849b3c5765e36e5c70e6294498271_l3.png)

Solch einen Körper nennt man Parallelepiped .Spatprodukt im ℝ 3.In diesem Arbeitsmaterial geht es um das Spatprodukt von Vektoren.In diesem Video wird erklärt, was ein Skalarprodukt ist und wie man es berechnet. Das Spatprodukt det ist ein Produkt von drei Vektoren im ℝ 3: det: ℝ 3 × ℝ 3 × ℝ 3 → ℝ. Außerdem können wir aus 3 Punkten die Fläche von Körpern berechnen. Das Volumen einer Pyramide mit Grundfläche G G und Höhe h h ist gegeben durch: V = 1 3 ⋅ G ⋅ h V = 1 3 ⋅ G ⋅ h. Die Kombination aus Skalarprodukt und Kreuzprodukt in der Folgendenform wird als Spatprodukt bezeichnet. Spatprodukt = (a×b)·c. Den Winkel φ .KURZ ERKLÄRTVOLUMEN EINER PYRAMIDE. Das Spatprodukt ist eine Kombination aus Skalarprodukt und Vektorprodukt mit 3 Vektoren.Schlagwörter:SpatproduktVektorprodukt Die Antwort ist „Ja“ – es gibt sogar zwei Produkte von Vektoren: das Skalarprodukt und das Vektorprodukt.Der Spatprodukt-Rechner ermöglicht es Ihnen, das Spatprodukt aus 3 Vektoren zu berechnen und die Berechnungsschritte zu erhalten. Was ist das Spatprodukt und wie wird es berechnet. Dazu wird die Variante über Kreuzprodukt bzw.Definition
Spatprodukt: Herleitung, Berechnen & Beispiel
Diese Verschiebung des Punktes wird Vektor genannt.Schlagwörter:SpatproduktSkalarprodukt
Spatprodukt

Schlagwörter:SpatproduktSkalarprodukt
Spatprodukt ⇒ ausführliche und verständliche Erklärung
Du berechnest es, in dem du die drei Vektoren nebeneinander in eine Matrix schriebst und ihre Determinante ermittelst. Das machst du zum Beispiel mit der Regel von Sarrus . Zur Berechnung geben Sie die Werte der drei Vektoren ein, dann klicken Sie auf den Button ‚Rechnen‘.Eine Kombination aus Skalarprodukt und Vektorprodukt ist das aus je drei Vektoren gebildete Spatprodukt.Das Spatprodukt (auch gemischtes Produkt) ist das Skalarprodukt eines Vektors mit dem Kreuzprodukt (auch Vektorprodukt) zweier anderer Vektoren. Als Rechtssystem bzw. Sein Betrag ist somit gleich dem Volumen des aufgespannten . Das skalare Produkt wird auch inneres Produkt genannt und .Das Spatprodukt kannst Du auf zwei Arten berechnen.Produkte von Vektoren Hier werden die verschiedenen Produkte, die in der Vektorrechnung angewendet werden, vorgestellt: Das skalare Produkt, vektorielles Produkt und das Spatprodukt. In dieser Lerneinheit betrachten wir die Flächen von Parallelogramm und Dreieck sowie die Volumina von Spat und Pyramide. Diese sind immer paarweise kongruent (deckungsgleich). Um es von anderen Produkten, insbesondere vom Skalarprodukt, zu unterscheiden, wird es im deutsch- und englischsprachigen Raum .deEmpfohlen auf der Grundlage der beliebten • Feedback
Spatprodukt
Zur Berechnung geben Sie die Werte der drei Vektoren ein, dann klicken Sie auf .Alles zum Thema 10. Aufgabe zum Vektor- und Spatprodukt Mit einem Vektor kannst du von einem Ausgangspunkt alle Punkte im Raum .deSpatprodukt Aufgaben / Übungen – Gut-Erklärt. Auch wenn das Skalarprodukt von zwei Vektoren nicht 0 ergibt, kannst du diese Art der Vektor Multiplikation nutzen, um etwas über die Lage der Vektoren zueinander herauszufinden. Das Spatprodukt lässt sich ferner zur Berechnung des Abstands eines Punktes von einer Ebene und des Abstands zweier zueinander windschiefer Geraden anwenden. Das Kreuzprodukt, auch Vektorprodukt, vektorielles Produkt oder äußeres Produkt, ist eine Verknüpfung im dreidimensionalen euklidischen Vektorraum, die zwei Vektoren wieder einen Vektor zuordnet.Komplanarität eines Vektors.Schlagwörter:SkalarproduktVektorprodukt Ist das Spatprodukt 0, so sind die Vektoren linear abhängig.
- Hot Tubs For Sale In Louisville, Kentucky
- Postleitzahl Freckleben – Malerfirma Kellner Aschersleben Freckleben
- Braun 6510 Flex Us Anleitung , Seite 2 von Braun 6510 flex us Bedienungsanleitung
- Historia De The Misfits | Misfits
- Nürnberger: Adresse _ Rentenversicherungen: Übersicht
- How Many Calories In An Egg? Everything You Need To Know
- Destiny 2 European Dead Zone Lost Sector Locations
- Buckenham Blast Cleaning Services
- Fest Der Allerseligsten Jungfrau Maria Vom Berge Karmel
- Pilates Bälle Sportgeräte , Pilates Geräte große Auswahl