NNKJW

XSB

The Law Of Large Numbers | Explained: the Law of Large Numbers in gambling casinos

Di: Jacob

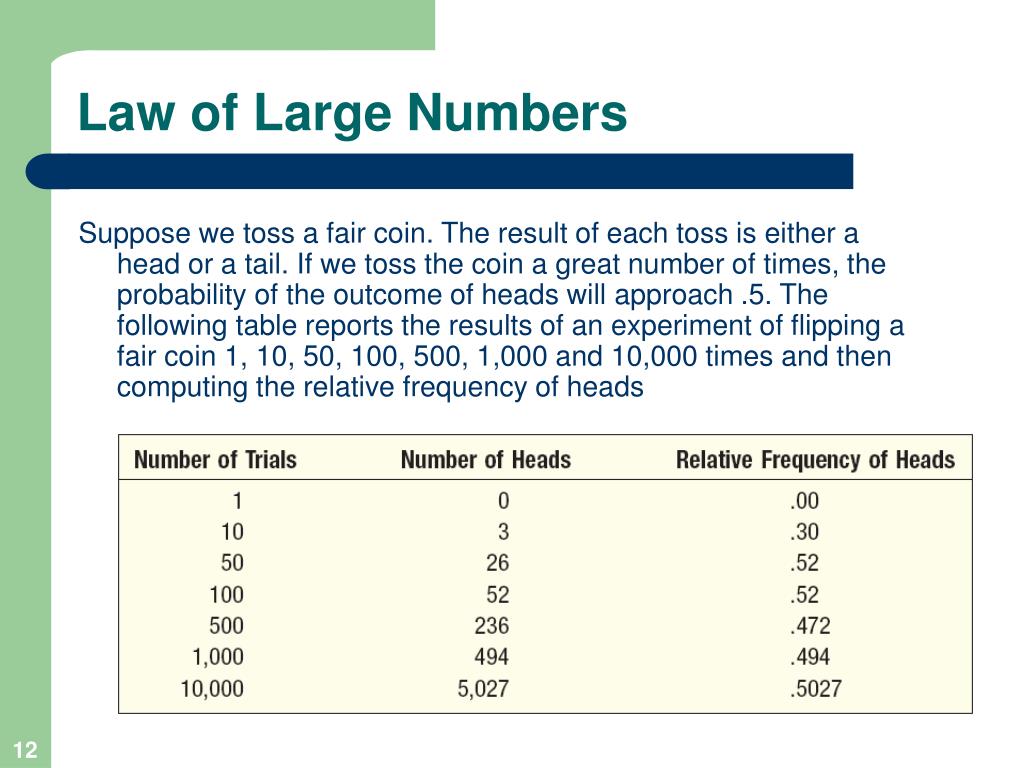
• Flip it 10,000 times.Come on, try it right now. an average), so let’s look at that.The law of large numbers is deduced from this theorem: It is first established that, as $ n \rightarrow \infty $, $$ {\mathsf E} \left ( \frac{X _ {1} + \dots + X _ {n} }{n} – a \right ) . New York: Academic Press 1968.The law of large numbers states that the sample mean converges to the distribution mean as the sample size increases, and is one of the fundamental theorems of . Kenneth Shultis, in Exploring Monte Carlo Methods (Second Edition), 2023 B.Just in time, on December 14, LVMH Moët Hennessy—Louis Vuitton SE announced an acquisition of Belmond’s public equity at $25 per share.Andrew Harnik / Getty Images file.Adler A, Matuła P (2018) On exact strong laws of large numbers under general dependence conditions. Roughly, the central limit theorem states that the distribution of the sum (or average) of a large number of independent, identically distributed variables will be approximately normal, regardless of the underlying distribution. At the top of this article, I mentioned that the weak Law of Large Numbers is noteworthy for what it does not say as much as for what it does say. The literature on the LLNs is of epic proportions, as this concept is indispensable in probability and statistical theory and their . Denote \(B=B^{H}\) when \(H=\frac{1}{2}\).The Law of Large Numbers (LLN) is one of the single most important theorem’s in Probability Theory.Sometime around 1687, the 32 year old first-born son of the large Bernoulli family of Basel in present day Switzerland started working on the 4th and final part of his magnum opus titled Ars Conjectandi (The Art of the Conjecture). But 7 heads would not surprise us. Google Scholar.Video ansehen8:59The law of large numbers just says that if we take a sample of n observations of our random variable, and if we were to average all of those observations– and let me define another variable.What is the Law of Large Numbers? In statistics and probability theory, the law of large numbers is a theorem that describes the result of repeating the same experiment a large number of .The laws of large numbers (LLNs) provide bounds on the fluctuation behavior of sums of random variables and, as we will discuss herein, lie at the very foundation of statistical . Probab Math Stat 38(1):103–121.Video transcript:How does an insurance company decide how much to charge for car insurance?How do casinos set up payout structures to make sure that they mak.This percentage is expressed from 0 to 100% and will always be lower than the full 100%.人们发现，在重複 .The Weak and Strong Laws of Large Numbers.The Law of Large Numbers By Elena Llaudet, co-author of Data Analysis for Social Science: A Friendly and Practical Introduction (Princeton University Press, 2022) The law of large numbers states that as the sample size increases, the sample mean of X approximates the population mean of X. When applied to the sample mean, what the law . While the weak law of large numbers establishes convergence of the sample mean, in probability, the strong law establishes almost sure . This explains the law of large numbers and how this law applies to gambling casinos.Law of large numbers, in statistics, the theorem that, as the number of identically distributed, randomly generated variables increases, their sample mean (average) approaches their theoretical mean. However, the law of large numbers also proves mathematically that if you were to toss that same coin 10,000 times, you would be very close to the 50% inherently probable outcome.In the 4th part, Bernoulli focused on .Lecture 9: The Strong Law of Large Numbers 49.The weak Law of Natural Numbers expressed using even lesser ink (Image by Author) Busting some myths about the weak LLN. It all started with Jacob Bernoulli.What is the Law of Large Numbers (LLN)? The LLN states that as the size of a sample drawn from a population increases, the sample mean approaches the population .在概率论中，大数定律（law of large numbers）是在对多次重复试验下频率稳定到概率这一问题的处理下发展出来的，它是概率论中最深刻的极限定理的一个结果。Autor: Sal KhanGeschätzte Lesezeit: 4 min

Law of large numbers

comEmpfohlen auf der Grundlage der beliebten • Feedback

Law of Large Numbers: Definition + Examples

The law of large numbers has a very central role in probability and statistics. The weak LLN is often misinterpreted to . In other words: in the long run random events tend to average out at the expected value. Effectively, the LLN is the means by which scientific endeavors have even the possibility of being reproducible, allowing us to study the world around us . An Opinion Poll.

Law of Large Numbers

To illustrate this theorem, we can use the interactive graph below to draw random .The Laws of Large Numbers.The Law of Large Numbers is a publication with original writings by artist Rindon Johnson that accompanies the exhibitions Law of Large Numbers: Our Bodies at SculptureCenter, New York, and Law of Large Numbers: Our Selves at Chisenhale Gallery, London. For example, knowing that a fair coin’s long-term average is 50% heads does not predict the outcome of the next coin toss. It states that if you repeat an experiment independently a large number of times and average the result, what you .The law of large numbers is one of the most intuitive ideas in statistics, however, often the strong and weak versions of the law can be difficult to understand.However, for an infinite variance, the proof of the law is considerably more complex that than given . The sample mean is the most obvious example of a statistic that relies on averaging (because that’s what the mean is.

PPT - A Survey of Probability Concepts PowerPoint Presentation, free ...

: Moment inequalities for the maximum cumulative sum.In these tutorials, we will cover a range of topics, some which include: independent events, dependent probability, combinatorics, hypothesis testing, descriptive statistics, random . Theorem 1 (Bernoulli) Let \(p_{0}\) be the occurrence probability of an . It is safe to think of Ω = RN× R and ω ∈ Ω as ω = ((xn)n≥1,x) as .The law of large numbers is a mathematical law that applies to many different sample statistics, but the simplest way to think about it is as a law about averages. In many practical applications, the number of the experiments depends on chance.Law of Large Numbers. An election is to be conducted for President of the .The Law of Large Numbers basically says that the more times you repeat a random experiment (like flipping a coin), the closer the average outcome (like the percentage of heads) will get to the expected value (50% heads and 50% tails, in this case).The law of large numbers states that as a sample size becomes larger, the sample mean gets closer to the expected value. 大数定律很重要，因为它“說明”了一些随机事件的均值的长期稳定性。 They have a history going back over 300 years.The law of large numbers for the maximum of almost Gaussian log-correlated fields coming from random matrices.A law of large numbers states that the average of the first n terms of a sequence of random variables is practically constant if n is large enough.2 million, and revenue hitting £2. 41, 1227–1234 (1970 .Plus formellement, elle signifie que la moyenne empirique, calculée sur les valeurs d’un échantillon, converge vers l’espérance . The law of large numbers means that with larger numbers of trials of an experiment the observed empirical probability of an event will approach the . En mathématiques, la loi des grands nombres permet d’interpréter la probabilité comme une fréquence de réalisation, justifiant ainsi le principe des sondages, et présente l’espérance comme une moyenne. Published: 13 February 2018; Volume 173, pages 157–209, (2019) Cite this article; Download PDF.

PPT - Section 6.3 ~ Probabilities With Large Numbers PowerPoint ...

In fact, it is possible to demonstrate that this is not the case and that the convergence is quasicertain.A Law of Large Numbers (LLN) is a proposition that provides a set of sufficient conditions for the convergence of the sample mean to a constant. Technical Report, Florida State University (1969) Serfling, R. J Theor Probab .Definition: Law of Large Numbers.: Probability inequalities and convergence properties for sums of multiplicative random variables. It should be noted that the law of large numbers also holds even for an unbounded variance σ 2 (Cremér, 1947). Typically, the constant is the expected value of the distribution .

大数定律

2 Other Subtleties. Connecting Johnson’s rigorous and poetic writing practice with the larger themes of the exhibitions, the book serves . Though the theorem’s reach is far outside the realm of just probability and statistics. Forearmed with this knowledge, it’s now time to explore some of the potential applications during your next casino session!When we do an experiment a large number of times the average result will be very close to the expected result. In ihrer einfachsten Form besagen diese Sätze, dass sich die relative .The law of large numbers underlines the fact that there persists a probability, even if very small, of substantial deviation between the empirical mean of a series of events and its expected value.

Law of large numbers | Probability and Statistics | Khan Academy - YouTube

Let me explain what I mean by that.The law of large numbers, or LLN for short, [1] is a theorem from statistics. It states that, as a probabilistic process is repeated a large number of times, the relative . Let Sn = X1 + X2 + ⋯ + Xn be the sum of the Xi.He proved it for a sequence of random events, providing the following temporal interpretation.It is for this reason that the term weak law of large numbers is used. In simpler words: In the short run, randomness can seem unpredictable and chaotic, but given .The Law of Large Numbers says you are more likely to be close to what you expect (here within \$10) for the larger number of trials « Previous 7.What is the Law of Large Numbers in Statistics? The Law of Large Numbers is a cornerstone concept in statistics and probability theory.One of the basic laws of probability theory is the law of large numbers for sequences of random phenomena, originally published in the posthumous work of Jakob Bernoulli in 1713 (Bernoulli 1986).The pattern of damage shows that many of the areas burnt are set back from the border, which reflects the use of large numbers of unguided weapons by Hezbollah.orgLaw of Large Numbers: 4 Examples of the Law of Probabilitymasterclass.With the Chebyshev Inequality we can now state and prove the Law of Large Numbers for the continuous case.在數學與統計學中，大数定律（英語： Law of large numbers ）又称大数法则、大数律，是描述相当多次数重复实验的结果的定律。The law of large numbers states that an observed sample average from a large sample will be close to the true population average and that it will get closer as the sample grows larger. The law of large . The chapter describes the conditions on { vn } under which ζ n 0 implies ζ n ⇒ 0. Let us now work on a sample space Ω.The three limits can be seen as the laws of large numbers associated with the self-attracting diffusion., Xn be an independent trials process with a continuous density function f, finite expected value μ, and finite variance σ2.Law of large numbers Sayan Mukherjee We revisit the law of large numbers and study in some detail two types of law of large numbers 0 = lim n!1 P j S n n pj 8>0; Weak law of larrge numbers 1 = P !: lim n!1 S n n = p ; Strong law of large numbers Weak law of large numbers We study the weak law of large numbers by examining less and less restrictive conditions .根据这个定律知道，樣本數量越多，則其算术平均值就有越高的機率接近期望值。1 – The Rules of Probability Next 7.

PPT - Basics of probability in statistical simulation and stochastic ...

Geschätzte Lesezeit: 7 min A Southern California school district involved in an ongoing legal battle with the state over the district’s gender-identity policy sued Democratic . The central limit theorem and the law of large numbers are the two fundamental theorems of probability. This law asserts that as the number of trials or samples increases, the observed outcomes tend to . It states that if a random process is repeatedly observed, then the average of the observed values will be stable in the long run.The laws of large numbers (LLNs) provide bounds on the fluctuation behavior of sums of random variables and, as we will discuss herein, lie at the very foundation of statistical science.The law of large numbers is one of the most important theorems in probability theory.2 The first Borel-Cantelli lemma.While the Law of Large Numbers can provide insights into long-term averages and expectations, it does not predict specific future events.Law of large numbers (video) | Khan Academykhanacademy. Braziel sold the call .它表明，使用概率公理化定义的某些概率在实际生活中和一般意义下的频率近似概率是一致的，从而说明了使用公理化定义概率 . In this video, I.Als Gesetze der großen Zahlen, abgekürzt GGZ, werden bestimmte Grenzwertsätze der Stochastik bezeichnet.

PPT - Law of Large Numbers PowerPoint Presentation, free download - ID ...

THE STRONG LAW OF LARGE NUMBERS. Article MathSciNet MATH Google Scholar Anh VTN, Hien NTT, Thành LV, Van VTH (2021) The Marcinkiewicz–Zygmund-type strong law of large numbers with general normalizing sequences.Those numbers also showed a strong year, with profits increasing more than 17% to £1 billion, average profit per equity partner reaching £2.The law of large numbers helps us make predictions about the long-term behavior of a random variable based on a large number of experiments.

Explained: the Law of Large Numbers in gambling casinos

Gesetz der großen Zahlen

Probability Theory and Related Fields Aims and scope Submit manuscript The law of large numbers for the maximum of almost Gaussian log .Wald’s Equation. For simplicity, we throughout let C stand for a positive constant which may depend on \(H,\theta ,\nu \) and its value may be different in different appearance, and this assumption is also suitable . To motivate our study of the Law of Large Numbers we begin with an example.These materials demonstrate the law of large numbers in terms of proportions and averages, for a variety of processes modeled by different distributions and point out the .Visualisation de la loi des grands nombres.

Proof of the Law of Large Numbers Part 1: The Weak Law

The law informs us about the expected distribution of outcomes over a large number of trials, not .3 – Simulating Probabilities » This means that as the number of observations increases, the average of the observed values will get closer and closer to the expected .The discovery of the Weak Law of Large Numbers. We expect 5 heads. Example: Flipping a coin • Flip it just 10 times. With a RTP of 98% (house advantage is 2%), the return to player for every £100 would be £98 and the house earning £2 of every £100 in bets.