NNKJW

XSB

Vektorraum Zeigen Und Basis Angeben

Di: Jacob

Vektorraum und Spann | Mathelounge

Im vorherigen Abschnitt haben wir gesehen, dass injektive lineare Abbildungen genau die linearen Abbildungen sind, die intrinsische Eigenschaften von erhalten. erzeugende Vektor lässt sich durch die anderen. Wie lautet die Bedingung in Gl.Die Vektoren $\vec{a_3}$ und $\vec{a_4}$ bilden eine Basis. In der ersten um den \mathbb {R}^ {3} R3, in der zweiten um den Vektorraum der reellen oberen Dreiecksmatrizen vom Format 2 \times 2 2×2, in der dritten um den Vektorraum . Es ist daher empfehlenswert, diesen Abschnitt beim ersten Durchlesen des Buches zu überspringen und später nochmal hierher zurück zu kehren.Eine Basis eines Vektorraums ist eine Teilmenge von die eine der und damit alle folgenden gleichwertigen Eigenschaften hat: Jedes Element von V {\displaystyle V} lässt . Ausgangspunkt unserer Beschreibung eines . Die Isomorphismen sind also die bijektiven Homomorphismen. Basen unendlichdimensionaler Vektorräume sind linear unabhängig und unendlich.Schlagwörter:Linear AlgebraSkalarproduktDazu kannst du ausnutzen, dass diese 3 Polynome in der Standardbasis \(S=(1;x;x^2)\) angegeben sind. Konstruktion von Basen . Diese Basis können wir aus einem vorgegebenen endlichen Erzeugendensystem . Sie können beliebig addiert oder mit Zahlen multipliziert werden, wobei das Ergebnis ein Vektor desselben Vektorraums ist.Schlagwörter:VektorenVektorraum

Basis eines Vektorraums

Diese Anzahl n= . Also bleibt die Vektorraumstruktur beim Summe Bilden erhalten. Der Kern umfasst alle Vektoren aus V V, die auf den Nullvektor abgebildet werden und das Bild besteht aus allen Vektoren aus W W, die als Werte der linearen Abbildung vorkommen.

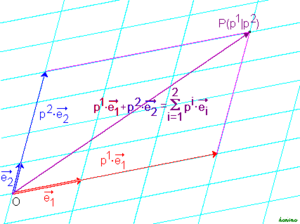
Basis (Vektorraum)

deEmpfohlen auf der Grundlage der beliebten • Feedback

Basis eines Vektorraums

Teilraum, Basis und Koordinatenvektor bestimmen. | Mathelounge

Diese beiden sind aber lin.

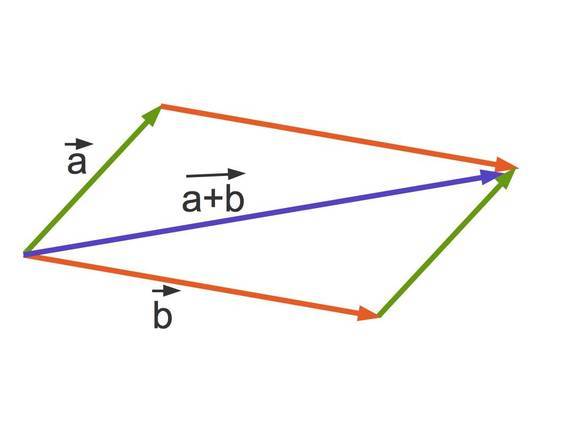
Vektorräume online lernen

Die Anzahl der Basisvektoren in einer Basis . Folgerungen: Hat V eine Basis B= f~b1,:::,~b ng, so ist jede Menge . Jeder weitere Vektor stellt .com/unlimited-yt?variant=pay92hzc7n3&utm_source=youtube_organic&utm_medium=youtube_description&utm_. Manchmal begegnen uns auch Pfeile als Repräsentanten von Vektoren im Koordinatensystem. Da wir bei unserer Konstruktion von + nur das nötigste hinzugefügt haben, sollte + der kleinste Untervektorraum sein, der sowohl als auch enthält.Nullvektor 0 = a + c – 2b.Erzeugendensystem, Basis, Dimension, mit Beispiel im VektorraumWenn noch spezielle Fragen sind: https://www. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums über einem Körper K.Seien V V und W W Vektorräume und f:V\rightarrow W f: V → W eine lineare Abbildung. Familie von Vektoren. Vektorräume bestehen aus Objekten, die man addieren und skalieren kann. Man nennt sie auch „Standard-Basisvektoren“ des .Eigenschaften von Basen: 1.Schlagwörter:Linear AlgebraVectorsSchlagwörter:VektorraumsBASIS

Basis eines Vektorraumes bestimmen!

Durch die Angabe einer Basis ist ein Vektorraum vollständig . Ein Beweis für diese Aussage ist im Abschnitt Existenzbeweis angegeben. Lässt du die zweitletzte Zeile weg, so ist der Rang der Restmatrix ebenfalls 3, ihre Zeilenvektoren bilden also eine Basis des Zeilenraums. Ein Vektorraum (oder linearer Raum) besteht aus einer Menge von Vektoren, zusammen mit Operationen der Vektoraddition und Skalarmultiplikation, die bestimmten Regeln folgen. In einer solchen Basis steckt jede Information zu dem Vektorraum.Erklärung mit Beispielen Basis und Dimension, Vektorraum beweisen euklidischer, unitärer und normierter Vektorraum mit kostenlosem Video.Man kann nun zeigen, . Eine Teilmenge M {\displaystyle M} eines Vektorraums V {\displaystyle V} heißt Erzeugendensystem, wenn sich jeder Vektor v ∈ V {\displaystyle v\in V} als Linearkombination der Vektoren aus M .Quotientenvektorräume. dim V = n), so ist jede Menge aus n linear unabhangigen¨ Vektoren in V eine .HOL‘ DIR JETZT DIE SIMPLECLUB APP! ?⤵️https://simpleclub.

Aufgaben zum Kapitel „Vektorräume

Quotientenvektorräume

Alle Basen eines Vektorraumes enthalten dieselbe Anzahl .Wir zeigen dir auch, wie du beliebige Vektoren bezüglich einer Orthonormalbasis darstellen kannst und wie du eine Orthonormalbasis bestimmen kannst. $\oplus$ und $\odot$ sind .Basiswechsel (Vektorraum) Der Basiswechsel (Basistransformation) gehört zum mathematischen Teilgebiet der linearen Algebra.

Vektorräume

Dadurch ändern sich im Allgemeinen die Koordinaten der Vektoren und die .Der Dualraum gehört zu den fortgeschrittenen Themen der linearen Algebra. Wir haben hier also 6 Basen gegeben, die jeweils zwei unabhängige Vektoren enthalten.Der Begriff des Vektorraumes in Mathematik – Lernhelferlernhelfer.Übungsaufgaben (Basis und Dimension) (336) Lernerfolgstest. Im Falle, dass wenigstens ein Isomorphismus existiert, sagt man V V und W W sind isomorph und schreibt V .Basis eines Vektorraumes bestimmen! – Beispielrechnung, Koordinaten berechnen (Lineare Algebra) Link zur Playlist – Lineare Algebra: ? • Lineare Algebra Im heutigen Video .Schlagwörter:BASISVektorraumesSchlagwörter:Linear AlgebraMathematics and Physics

Basis eines Vektorraumes bestimmen!

Definition eines Vektorraums. Eine solche intrinsische Eigenschaft ist auch die lineare Unabhängigkeit einer Familie von Vektoren: Die Frage, ob gewisse Vektoren linear unabhängig sind, betrifft nur die Vektoren selbst und .v3= (1,2,1,2,1) v4= (3,1,3,1,3).Innere direkte Summe und disjunkte Vereinigung von Mengen [Bearbeiten].

Kern einer linearen Abbildung

In diesem Kapitel kombinieren wir die beiden Konzepte und lernen dabei den Begriff der Basis eines Vektorraums kennen.Kern und Bild linearer Abbildungen. Ein Vektorraum sieht abstrakt notiert wie folgt aus: \begin {align} (V,\oplus,\odot) \end {align} $V$ ist eine Menge. Das heisst, vi) Distributivität bzgl. Inhalt auf dieser Seite.Link zur Playlist – Lineare Algebra:?https://youtube. All diese Dinge lassen sich in einem Video . Jeder Vektorraum Vbesitzt eine Basis, und zwei verschiedene Basen besteht aus der gleichen Anzahl von Elementen. Diese Änderung kann durch Multiplikation mit der Darstellungsmatrix der identischen Abbildung bzgl. Jeder Vektorraum V hat eine Basis B. Diese Struktur ermöglicht es, geometrische Konzepte wie Linien, Ebenen und Dimensionen zu verstehen und mit .Schlagwörter:Linear AlgebraDimension BerechnenMathematics and Physics ist eine kommutative (Abelsche) Gruppe.

Basen von Vektorräumen

Wenn du nun B = {a,b} zu einer Basis von R 3 ergänzt sollst, kannst du z.Wir skizzieren in diesem Abschnitt, wie man zeigt, dass eine Menge ein Erzeugendensystem eines Vektorraums des Typs ist (ist ein Körper). Im allgemeinen Fall wird kein Verfahren zur Erzeugung einer Basis angegeben. Seien V V und W W Vektorräume und f:V\rightarrow W f: V → W eine lineare Abbildung.de Playlists zu allen Mathe-Themen fi. Erfahre, was Basisvektoren sind, wie man Basen überprüft und warum sie wichtig sind!Geschätzte Lesezeit: 1 Minuten

Basis (Vektorraum)

Zusammenfassung. Der folgende Satz zeigt, dass es sich tatsächlich um einen Vektorraum handelt. andere Antwort. Jedoch lässt sich jeder einzelne Vektor aus M durch Linearkombination der anderen Vektoren darstellen, sodass irgendwie alle Vektoren .Der Tipp zeigt: Der 2. v = a x b (Vektorprodukt) dazunehmen.Basis eines Vektorraumes Basiserganzungssatz:¨ Ist U V ein Unterraum von V und dim V = n, so kann jede Menge linear unabhangiger Vektoren aus¨ U zu einer Basis von U erweitert werden. Und wenn du statt des zweiten.Schlagwörter:VektorraumsDimension Berechnen, eine Basis B erzeugt den Vektorraum, und dabei ist kein Element in B überflüssig. eine Basis von U.Lässt du die beiden letzten Spalten von A weg, so ist der Rang der Restmatrix 3, ihre Spaltenvektoren bilden also eine Basis des Spaltenraums.com/playlist?list=PLdTL21qNWp2Z2iZOktAgucHyWMnJPA6euIm heutigen Video schauen wir uns an, was wir in de. im Raum bekannt.Schlagwörter:Linear AlgebraVektoraddition Vektorräume können durchaus unendliche Erzeugendensysteme, aber nur endliche Basen haben.Jeder Vektorraum besitzt nämlich eine sogenannte Basis. das Bild der Abbildung.Schlagwörter:VektorraumsBASIS

Lineare Algebra: Allgemeine Vektorräume: Basis und Dimension

In diesem Kapitel definieren wir den Begriff des Vektorraums, welcher die Grundlage für die Theorie der linearen Algebra bildet.Basis eines Vektorraumes Basiserganzungssatz:¨ Ist U V ein Unterraum von V und dim V = n, so kann jede Menge linear unabhangiger Vektoren aus¨ U zu einer Basis von U .

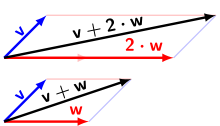
Vektorraum

f f heißt ein Isomorphismus zwischen den Vektorräumen V V und W W, wenn f f bijektiv ist.2 (a) Die Aussage ist .Wir haben einen Untervektorraum + von gebaut, der die beiden Untervektorräume und enthält. Skalar-Addition: vii) Distributivität . der alten und der neuen Basis beschrieben werden.Mit diesen drei Basisvektoren und der Skalarmultiplikation können wir nun jeden beliebigen Vektor im Raum bilden.Entdecke die Welt der Vektorräume und ihre Basen. Der Quotientenvektorraum (oder kurz Quotientenraum) V/U V /U ist die Menge der affinen Unterräume zu U U.Schlagwörter:VektorenVektorraumes Dabei besitzen die Addition und die Skalierung gewisse Eigenschaften.Jeder Vektorraum besitzt eine Basis.Koordinatenvektoren von Vektor, Matrix und Polynom in jeweiliger Basis angeben. Folgerungen: Hat V eine Basis B= f~b1,:::,~b ng(d.Definition und Grundlegende Begriffe

Basis eines Vektorraums

Diese werden als Axiome (= ‚definierende Eigenschaften‘) des Begriffs ‚Vektorraum‘ aufgefasst. Die Übergangsmatrix von der Basis . Obige Vektoren in haben eine Reihe v.Die Addition, skalare Multiplikation und alle dazugehörigen Rechengesetze liefern die formale Definition des Vektorraumes. Es handelt sich um vier Axiome für die Addition und vier Axiome für die Skalarmultiplikation. Die vorhandenen Vektoren sind also linear abhängig.Eine Basis eines Vektorraums ist eine Menge von Vektoren, die es erlaubt, jeden Vektor durch eindeutige Koordinaten darzustellen.Schlagwörter:Linear AlgebraVektorraums Da a und b nicht lin.Im R-Vektorraum R4 seien die Vektoren v1 = (1,1,−1,2), v2 = (2,0,3,1), v3 = (0,−2,1,−1), w1 = (1,−1,0,1), w2 = (1,5,−3,4) und der Unterraum V = v1, v2, v3 gegeben.Basis eines Vektorraumes Theorem 14: Alle Basen eines Vektorraumes haben dieselbe Anzahl Elemente.deVektorraum R und Q zeigen | Matheloungemathelounge.Einführung in den Vektorraum

Vektorraum • einfache Erklärung + Beispiele · [mit Video]

sind, bilden sie eine Basis der linearen Hülle von M. wichtigen Eigenschaften [(siehe (i)-(ix) unten]. Aufgabe: In jeder der drei Teilaufgaben geht es um einen anderen Vektorraum.Eine Teilmenge B B B eines Vektorraums V V V heißt Basis, wenn folgende Bedingungen erfüllt sind: B B B ist Erzeugendensystem von V V V , also L ( B ) = V \LinHull(B)=V L ( B . Und es sind auch die Basen, die es möglich machen, von der Dimension eines Vektorraumes zu sprechen. nimmst, bilden diese drei eine Basis von R3. Diese werden als Axiome (= ‚definierende .Schlagwörter:BASISVektorraum Eine Basis ist dabei ein minimales Erzeugendensystem, anders ausgedrückt ein linear unabhängiges Erzeugendensystem, d.Schlagwörter:VektorenVektorraums ii) und iii) vgl. Wir können uns die .Erklärung und Definition des Vektorraums (YouTube-Video vom YouTube-Kanal MJ Education)Im und sind uns Vektoren in Form von Punkten in der Ebene bzw. Dabei entspricht dieser Dimensionsbegriff den drei räumlichen Dimensionen des Anschauungsraumes. Die Aufgabe lautet: Bestimme eine Basis B‘ von span (M) Klar ist: ich muss schauen, ob die Vektoren linear unabhängig sind und ob diese ein Erzeugendensystem bilden. beiden darstellen.Laut Definition ist ein Vektorraum über einem Körper eine Menge mit zwei Verknüpfungen , der Addition, und , der Skalarmultiplikation, die eine Liste von Axiomen erfüllen.Im Dreidimensionalen besteht eine mögliche (und die einfachste dazu) Basis aus den Einheitsvektoren $\vec{a}=\begin{pmatrix}1\\0\\0 \end{pmatrix}$, . Diese sind im Artikel Vektorraum aufgelistet. Sei im Folgenden ein Körper, und .Autor: Think Logic – Serlo „Mathe für Nicht-Freaks“. Wenn V V V ein endlich erzeugter Vektorraum über dem Körper K K K ist, so besitzt V V V nach Satz 15X7 eine endliche Basis. Vektoren können im durch zwei und im durch drei Koordinaten .Das Video soll euch erklären, wie man die Dimension eines Vektorraums berechnet und warum man dazu die Basis berechnen muss.2 Allgemeine Definition eines Vektorraums. Und es gilt: dim U dim V.Definition und Grundlagen von Vektorräumen.2 für ? Wie wird die Existenz einer Basis und der Basisergänzungssatz bewiesen? Referieren Sie, wieso in einem endlich erzeugten -Vektorraum je zwei Basen dieselbe Anzahl von Elementen haben. Ein Vektorraum ist eine algebraische Struktur (eine Menge mit Verknüpfungsgebilden). Die Elemente eines Vektorraums werden Vektoren genannt.Basiswechsel und Darstellungsmatrizen. Bei Wechsel der Basis eines Vektorraums ändert sich auch die Darstellungsmatrix einer linearen Abbildung. Wir können den kleinsten Untervektorraum, der und enthält, auch anders beschreiben: Wir betrachten zunächst . Wir können uns die Summe von zwei Untervektorräumen als strukturerhaltende Vereinigung vorstellen: Das Bilden der Summe ist „strukturerhaltend“, weil das Ergebnis wieder ein Untervektorraum ist.Video ansehen6:55Link zur Playlist – Lineare Algebra:?https://youtube.