NNKJW

XSB

Why Can’T Two Vectors Span $\\Bbb R^3$?

Di: Jacob

Also, $(1,0,0),(0,1,0),(0,0,1),(2,3,5)$ are not linearly independent but they span $\mathbb{R}^3$. For example, $e_1,e_2,e_3,e_1+e_2$ span $\Bbb R^3$ however they are clearly linearly dependent. Two vectors absolutely cannot span R3.

Span and linear independence example (video)

(As Gerry points out, the last .Method You Can Use Because Your Vectors Happen to Be in $\Bbb R^3$ Where the Cross Product Is Defined: To verify your vectors are linearly dependent you could take . Show this is not a linear transformation. See if one of your vectors is a linear combination of the others.Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site

Solved a) Can two vectors span R3? Can they be

Can the Span of Three Vectors Be Contained in R^2?

I want to know the mathematical difference between linear independence and not being in the span.Why can’t two vectors span $\Bbb R^3$? 0. So I am wondering, by what you have said, that if 3 of the four vectors in the span are linearly independent (because there are 3 pivot columns), does that mean the .You’re right, because the dimension of R3 is 3 => R3 basis has 3 vectors.How to determine the span of two vectors in $\mathbb R^2$: $(4,2)$ and $(1, 3)$ Do I subtract them? I don’t how I’d solve this. Understand the concepts of . Take the cross product of the two remaining vectors to obtain a vector .Linear dependence does not imply that they do not span $\Bbb R^3$.Verify if three 3-dimensional vectors (v1:[. Three linearly independent vectors with real . Here’s some proofs. How to check if the columns of a given vector spans Rn.Consider two vectors $$ u_ {1} = \begin {bmatrix} -1 \\ 3 \\ 2 \\ \end {bmatrix},\quad u_ {2} = \begin {bmatrix} 6 \\ 1 \\ 1 \\ \end {bmatrix} $$.

The SpaceR3

linear-algebra; self-learning; Share . A linear combination of two (linearly independent) vectors will span a plane. Try to visualize it: a linear combination of one vector will be the scalar multiples of that vector. All I have to do is to put three vectors into a 3 by 3 matrix and perform elementary row . But this is easy — in fact, since most $(a,b,c)$ cannot. It may have three components but they are all multiplied by the same number λ so there is one-to-one . The vector space defined by this basis will have two dimensions as there are two basis . Linear Algebra Solution set equal to Span.The three vectors in your example is not independent because one of them is redundant since you can get the same span with just two of them (1,0,0) and (1,1,0), since (0,1,0) .$\begingroup$ Yes, when you’re talking about two planes in $\Bbb R^3$, the planes are orthogonal iff their normal vectors are orthogonal. A set of vectors span the entire vector space iff the only vector orthogonal to all of them is the zero vector.If R^n has a linearly independent subset of cardinality n+1 (a potential basis), it has a subspace isomorphic to R^(n+1) (the span of those n+1 vectors) we will call V^(n+1).

Why do we say that two vectors in $R^3$ cannot span $R^2$?

3Schlagwörter:Linear AlgebraSpan of Two Vectors in R3Linear Span

Is it possible for two vectors to span $\\mathbb{R}^3$?

I hope someone can help me. Follow edited Jul 17, 2023 at 13:30.If the two vectors are linearly independent (the two vectors aren’t scalar multiples of each other), then the two vectors will span a plane in R3. You actually have $4$ columns here, so all four don’t form a linearly independent set, but any three of them do and that means that all four form a spanning set.

Solved (1 point) Do the following sets of vectors span R3? | Chegg.com

If the two vectors are linearly . And the span of two of vectors could never span R3. In fact, the third vector (0 0 1 0) can be expressed . It turns out that you need are . It is true if and only if there. Last night I was thinking about how one could prove that four vectors cannot span $\mathbb R^5$, and the solution below is what I came up with. Thanks for helping. I always pick the third one, but let’s say this guy would be redundant, which means that the span of this would be equal to the span of these two, right? Because if this guy is redundant, he could just be part of the span of these two guys. d) Let T : P 4–>R 3 be defined by . A linear combination of two (linearly .

How to show that a set of vectors do not span $\\mathbb R^3$?

Span and linear independence example (video)

Determine if a set of vectors is linearly independent.The span of two vectors in $\mathbb{R}^2$ neither of which is zero vector, and which are not parallel, is-a point.Two vectors absolutely cannot span R3. If the vector is not in the span, does that mean it’s not linearly dependent? If it cannot be linearly dependent, why .Determine the span of a set of vectors, and determine if a vector is contained in a specified span.

Find a basis for the span of a set of vectors (either a subspace or a ...

In fact you could just keep adding columns all day to this and it’d still form a spanning set because the I can tell they don’t . In other words, adding a scaled .If we have two vectors in $R^3$, $v=(1,2,0)$ and $u=(5,3,0)$, and if we draw these vectors in $R^3$ they will be in the $xy$-plane or $R^2$ and also these two vectors . linear-algebra; vectors; Share. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the . I found the RREF and found that there were 3 pivot columns.The first three vectors $(1, 0, 0)^T, (0, 1, 0)^T, (0, 0, 1)^T$ already span $\Bbb R^3$ (in fact, they constitute an orthonormal basis) – so adding any more vectors to this collection (e.) B) Can four vectors span R 3? Can they be linearly independent? (Explain. Let us see if $u\in\langle u_1,u_2\rangle$.Can two vectors of 3-Tuples span $\mathbb R^3$? Ask Question Asked 6 years, 10 months ago. Modified 3 years, 10 months ago.Apologies in advance for any bad formatting etc. But projecting V^(n+1) into R^(n+1) gives an n+1 element linearly independent set in R^(n+1) that is not a basis.You want to find $(a,b,c)$ such that $(a,b,c)$ cannot be written as $x(-1,3,2)+y(6,1,1)$.For example, $\Bbb R^2$ is not spanned by $(1,0)$ and $(2,0)$, since the point $(1,1)$ is not in the span of $\{(1,0), (2,0)\}$ (which is the $x$-axis).The set of all ordered triples of real numbers is called 3‐space, denoted R 3 (“R three”). Stack Exchange Network. line in $\mathbb{R}^2$ not running through origin.]) will span $\mathbb{R}^3$. Writing these in a matrix and performing row . In my question the vectors are like this: \begin{b. Viewed 1k times 1 $\begingroup$ I’m just checking, but when we have $2$ vectors .I want to solve this question only using what’s from section 2A ( which basically talks about definition of linear combination of vectors, span of vectors, linear independence and dependence) and I can not find a fourth vector that satisfies the question. Thanks in advance. The vectors in this set are not linearly independent.So, this means if you have any set of vectors in $\mathbb{R}^{3}$, they can’t span $\mathbb{R}^{2}$ because they aren’t even in $\mathbb{R}^{2}$ — they each have .I need to show that these three vectors expand the vector space $\Bbb R^2$ and I don’t know how to show that the right way. so, i think the deal here is that if they did span r^3 then the three vectors must be .I have tried searching related posts here on stackexchange and elsewhere to find errors in my solution, however I did not . If so, you can drop it from the set and still get the same span; then you’ll have three vectors and you can use the methods you found on the web. This means that one vector can be written as a multiple of the other vector, and therefore their linear .Therefore, the vectors do not span R³.By scaling a vector v you only get vectors λv that are parallel to it.No, you need at least n vectors to span R n.Let’s say that that guy was a redundant one.Method You Can Use Because Your Vectors Happen to Be in $\Bbb R^3$ Where the Cross Product Is Defined: To verify your vectors are linearly dependent you could take the triple scalar product. all of $\mathbb{R}^2$.Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site Skip to main content . If 2 linearly independant vectors spanned R3, then the dimension of R3 would be 2! But feel free to .

Solved 6. a. Can 3 vectors in R4 be linearly independent? b. | Chegg.com

The operations of addition and scalar multiplication difined on R 2 carry over to .Normally, I know that this means no solution, but my professor has stated, The vector is not in the span of the other vectors.

Linear Algebra: Linear combination of Vectors - Master Data Science

Follow edited Sep 14, 2015 at 6:12.No, two parallel vectors cannot span R3 because they are linearly dependent.

3Blue1Brown

If you have a set of n n-element vectors, you can see if they are linearly dependent by calculating their .I understand it intuitively, and I know how to prove it geometrically, but what is the the algebraic proof of this fact.$\begingroup$ My issue was, in the question they set up a span of 4 vectors, and asked if it was true that they spanned R3. Stefan Bonde Nielsen Stefan Bonde Nielsen.

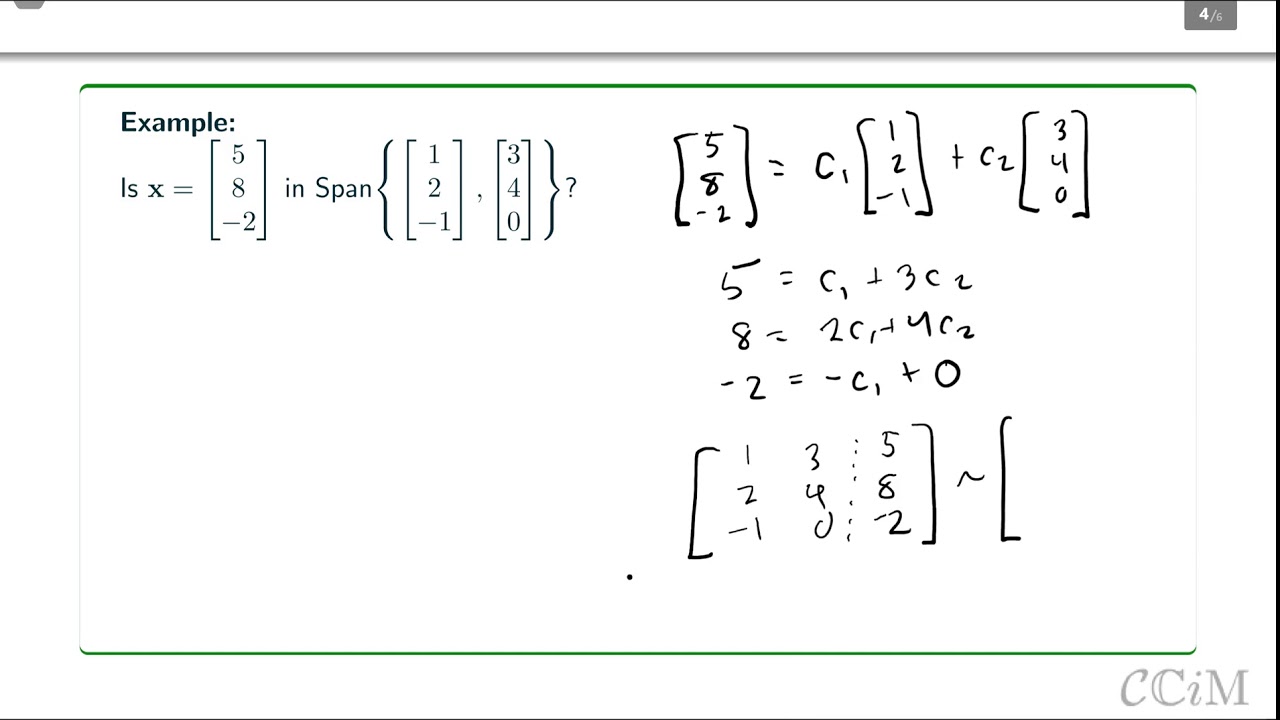
vector equations span - YouTube

If it is zero, the vectors are linearly dependent. Skip to main content. Show that T is a linear transformation. line in $\mathbb{R}^2$ running through origin. If you’ve covered the exchange lemma, that says that if I is an independent set and S is a spanning set you .

Explain why V is equal to a span

No, it is not possible to span the $\mathbb{R}^3$ with two vectors only.) c) Let T : P 2–>P 3 be defined by. What does it mean for a subset of a . checking if some vectors span $\Bbb R^3$ that actualy span $\Bbb R^3$ 3. show that the vectors u = [1 -2 3] v = [-4 8 -12] and z = [1 0 1] do not span r^3.If your third vector happens to be sitting on the span of the first two, then the span doesn’t change, you’re sort of trapped on that same flat sheet. asked Jul 17, 2023 at 12:51. Usually, we use the term vector to denote an element of a vector space, such as $\mathbb{R}^5$, while a matrix is a linear map between two vector spaces (at least, its representation in a certain basis). However, this is just a different concept from the linear algebra concept of orthogonal subspaces (which needn’t be orthogonal complements, by the way).

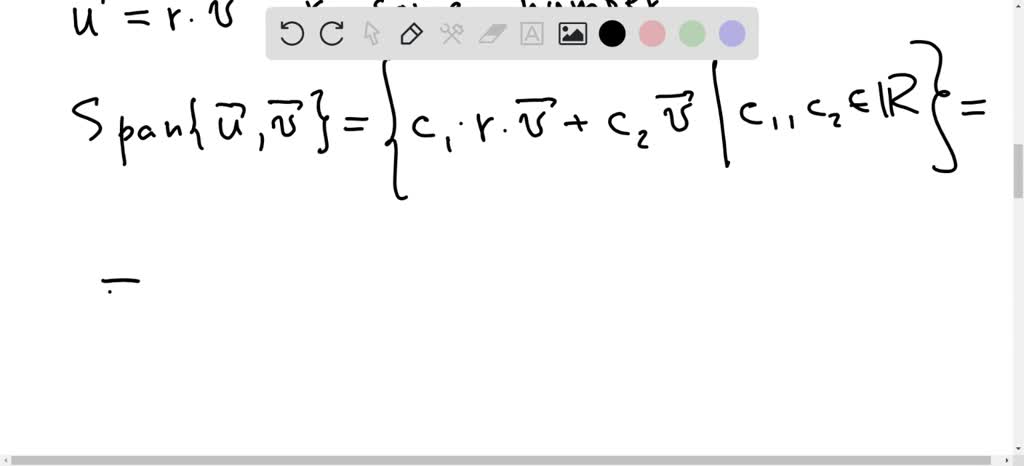
SOLVED: Prove: The space spanned by two vectors in $R^{3}$ is a line ...

as this is my first post. the fourth one $(1,1,1)^T$ in your post) does not affect the span.

Determine if a Vector is in the Span of Two Other Vectors in R3 (Yes ...

How would you go about showing that any two non-parallel vectors can form the basis of $\Bbb R^2$? I know that they will do: they form a linearly independent set because neither are multiples of each other (due to them being non-parallel), so they will form a basis.Find a linearly independent set of vectors that spans the same substance of $\mathbb{R}^3$ as that spanned by the vectors $\begin{bmatrix}2\\2\\-1\end{bmatrix}, \begin{bmatrix}-8\\-2\\5\end{bmatrix. Extending this to a basis yields a subspace isomorphic to R^(n+2).

Why do two linearly independent vectors span $\\mathbb{R}^2$?

194 1 1 silver badge 8 8 bronze badges.You are mixing up concepts.If three mutually perpendicular copies of the real line intersect at their origins, any point in the resulting space is specified by an ordered triple of real numbers (x 1, x 2, x 3). To see this, note that if we had $3$ linearly independent vectors which did not span $\mathbb R^3$, we could expand this to a collection of $4$ linearly independent vectors. When a span of set of vectors is equal to span of canonical basis with the same dimension.If three vectors can’t be written as linear combinations of each other, they span R 3.4$\dim\operatorname{span}(\{v_1,v_2\}) \le 2$ while $\dim(\mathbb{R}^n) = n$ for all $n$.Schlagwörter:Linear AlgebraSpan of Two Vectors in R3Span of 3 Vectors

linear algebra

Condition 2: Linear independence.At this point, it is clear the rank of the matrix is $3$, so the vectors span a subspace of dimension $3$, hence they span $\mathbb{R}^3$.I understand how to determine WHETHER a set of vectors span a space, but I’ve been given two vectors (1,2,3,4) and (17,17,17,17) and asked to find two more vectors such that the set of all these ve. By understanding the concept of a basis you will know that the $\mathbb{R}^3$ has dimension $3$ and .

Proving Span of $\mathbb{R}^2$ Using Sets of Vectors

Since eliminating just 1 more variable would have solved the system, we know that there’s 1 redundant vector in the set and there’s therefore 2 linearly independent vectors in the .

How to Know if Vectors Span R3

Well, you need two-element vectors for R 2 and three-element for R 3. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most .Yes, because $\mathbb R^3$ is $3$-dimensional (meaning precisely that any three linearly independent vectors span it).a) Can two vectors span R 3? Can they be linearly independent? (Explain.Any three linearly independent vectors in $\Bbb R^3$ will span $\Bbb R^3$.Beste Antwort · 8Let $u=\begin{bmatrix}a\\b\\c\end{bmatrix}$, with $a,b,c\in\mathbb R$. They are radically different things, but they are often introduced in the same framework and so people get .For instance, $(1,0,0)$ and $(0,0,1)$ are linearly independent but they do not span $\mathbb{R}^3$.