NNKJW

Zufallsexperimente, Zufallsvariable Und Stochastische Prozesse

Di: Jacob

Zufallsexperiment ⇒ einfach und verständlich erklärt – . Zufallsexperimente – einstufig und mehrstufig. Die „Kunst des Vermutens“ – wie sich Stochastik übersetzen lässt – beschäftigt sich mit Ereignissen und Ergebnissen, die unterschiedlich häufig auftreten, wenn sich ein Vorgang wiederholt.1 Binomialverteilung.Obwohl einfache stochastische Prozesse . Das folgende einfache Beispiel dient dazu, die Problemstellung zu erläutern. Mehrstufige Zufallsexperimente: Worum geht es dabei? Mehrstufige Zufallsexperimente: Vom Rechnen mit Wahrscheinlichkeiten.Für die inhaltliche Be-stimmung und für das Verständnis stochastischer Grundbegriffe erweisen sich vor allem Zufallsexperimente, die Glücksspielen entlehnt sind, als sehr .degut-erklaert.In der Wahrscheinlichkeitstheorie bezeichnet ein Zufallsexperiment (auch Zufallsvorgang oder Zufallsversuch genannt) einen Versuch, der unter genau . Um diese rechnerisch handhaben zu können, werden den Ereignissen reelle Zahlen zugeordnet.Für beide Typen von Zufallsvariablen lassen sich Wahrscheinlichkeitsverteilungen bilden, die angeben, mit welcher Wahrscheinlichkeit die .!/W I! ; i 7! X i.Was bedeuten Konvergenzaussagen in der Wahrscheinlichkeitstheorie? Hier geht es darum zu verstehen, was passiert wenn man immer mehr Daten sammelt – also theoretisch unendlich viele.

Zufallsexperimente, Zufallsvariable und Stochastische Prozesse

Ein Zufallsexperiment ist ein grundsätzlich beliebig oft wiederholbarer Versuch, welcher unter identischen Bedingungen zu 2 oder mehreren nicht vorhersagbaren Ergebnissen führt.In diesem Anhang werden die elementaren Grundlagen zu Zufallsvariablen und stochastischen Prozessen zusammengestellt, die an verschiedenen Stellen des . Hierbei werden auf der x-Achse die verschiedenen Ausprägungen der Zufallsvariable und auf der y-Achse die zugehörigen Wahrscheinlichkeiten abgetragen.: binomial distribution).Unter einem Zufallsexperiment verstehst Du einen Vorgang, der die folgenden Eigenschaften erfüllt: Das Experiment kann beliebig oft wiederholt werden.Y i/ i2I Y i W ˝! ; i 2 I einen weiteren stochastischen Prozess gegeben, so heißen die beiden stochastischen Pro-zesse . die wichtigsten Definitionen und Sätze zu bedingten Erwartungswerten, Martingalen und Wiener- und Sprungprozessen .Ein stochastischer Prozess ist eine Folge von Zufallsvariablen \(\left( {X_{t} } \right)_{{t \in T}}\), in der \(T\) die Menge der Zeitpunkte bezeichnet, für die der Prozess . von einem Experiment, dessen .

Zufallsexperiment in der Stochastik – Testfragen/-aufgaben 1. Ganz schön komplex: .Zentrale Konzepte der Stochastik umfassen Zufallsexperimente, Ereignisse, Ergebnismengen und Wahrscheinlichkeiten.Habe beruflich viel zu tun mit Prozess-Simulation. von einem Experiment, dessen Ausgang nicht von vorneherein festgelegt ist wie z. Dabei ist das zeitlich jeweils nächste Ergebnis unabhängig von den zeitlich vorhergehenden . Der Ausgang ist bei jeder erneuten Durchführung absolut zufällig.Hast Du eine Folge von Zufallsvariablen X (t) gegeben, die von einem sich ändernden Parameter t abhängen, so sprichst Du von einem stochastischen Prozess. man wirft einmal eine Münze Mehrstufiges Zufallsexperiment: man führt es mehrfach durch, da hilft euch das Baumdiagramm!; z. Die Wahrscheinlichkeitsverteilung der Zufallsvariable gibt die Wahrscheinlichkeit zu jeder dieser Zahlen (und damit den zugehörigen Ergebnissen) an. Beeinflusst das Geschlecht ob eine Person eine Rot/Grün-Sehschwäche entwicklt oder nicht? Wir definieren zwei Ereignisse: Person ist männlich; Person hat eine Rot/Grün .Wahrscheinlichkeiten einfacher Zufallsexperimente berechnen, auswerten und verstehen. Wir besprechen folgende Unterthemen im Detail: Was ist eine Zufallsvariable? Diskrete Zufallsvariablen; Träger einer diskreten Zufallsvariablen; Wahrscheinlichkeitsfunktion einer diskreten Zufallsvariablen

Was sind Zufallsvariablen?

Stochastische Simulation von Zufallsvariablen und Punktprozessen.

Zufallsvariablen, stochastische Prozesse und deterministische Signale

Ziehst du jetzt eine Kugel aus der Urne, so handelt es sich um ein Zufallsexperiment.

Wahrscheinlichkeitsverteilung · Anschauliche Erklärung

Dies wird einige Vorteile mit sich bringen.

1 Zufallsvariablen und σ-Algebren Zu Beginn des Anhangs f¨uhren wir einige zentrale Begriffe ein.Dazu können stetige Zufallsvariablen in diskrete überführt werden.A Zufallsvariablen und stochastische Prozesse A.

Interpretation: Es sei !2 ein Ausgang unseres Zufallsexperiments. Ich suchte eine systematische Darstellung, in der auch die mathematische Sicht nicht zu kurz kommt (Markov-Prozesse etc.Zufallsvariablen, stochastische Prozesse und deterministische Signale.

Ein stochastischer Prozess ist eine Familie (X t) t2T von Zufallsvariablen auf (;F;P). Stochastische Prozesse bedeuten mehr als mehrdimensionale Zufallsvariablen, bei denen die zeitliche oder rӓumliche Entwicklung nicht betrachtet werden kann. Die Theorie der stochastischen Prozesse stellt eine wesentliche Erweiterung der Wahrscheinlichkeitstheorie dar und bildet die Grundlage für die stochastische Analysis.Ein stochastischer Prozess (auch Zufallsprozess) ist die mathematische Beschreibung von zeitlich geordneten, zufälligen Vorgängen.

Zufallsexperiment in der Stochastik

Zufallsvariablen und besitzt damit die selben Eigenschaften. Zufallsva-riablen beschreiben das Verhalten in Zufallsexperimenten,d. Die klassischen Beispiele für Zufallsexperimente sind Werfen einer Münze mit . Genauer gesagt kann ein Zufallsexperiment zu n verschiedenen möglichen Ausgängen führen, nämlich zu allen Ereignissen bis des Ergebnisraum . Zu Beginn des Anhangs f ̈uhren wir einige zentrale Begriffe ein.In diesem Anhang werden die elementaren Grundlagen zu Zufallsvariablen und stochastischen Prozessen zusammengestellt, die an verschiedenen Stellen des Lehrbuches benutzt werden. Neben der Klärung der verwendeten Nomenklatur werden in diesem Kapitel einige der später im .Zufallsexperimente Zufallsvariable und Stochastische Prozesse Information Technology · University of Ulm 1 Zufallsexperimente Zufallsvariable und Stochastische Prozesse.Zufallsvariablen und Verteilungen. Stochastische Modelle – OTH Regensburgfbim.Y i/ i2I nicht unterscheidbar, falls es .

Zufallsvariablen und stochastische Prozesse

man würfelt 5 mal

Zufallsexperimente: Münz- und Würfelwurf

Zufallsexperimente und Ereignisse¶ Experimente, die unter gleichen Bedingungen zu gleichen Ergebnissen führen, bezeichnet man als determiniert.Eine Wahrscheinlichkeitsverteilung ist eine mathematische Funktion, bei der jedem möglichen Wert eines Zufallsexperiments eine bestimmte Wahrscheinlichkeit zugeordnet wird. Eine Zufallsvariable ordnet jedem . Das wesentliche Kriterium . In diesem Artikel erklären wir dir alles zum Thema Zufallsvariablen und Verteilungen.In diesem Kapitel wollen wir den Begriff des “Stochastischen Prozesses” anschaulich und formal einf¨uhren.In der Mathematik werden Sachverhalte oft durch das Zufallsexperiment Ziehen einer Kugel aus einer Urne beschrieben. Mathematisch heißt das konkret: Wiederholst Du ein Zufallsexperiment beispielsweise n-mal, so kannst Du seine Ausgänge als Realisationen von n .deEmpfohlen auf der Grundlage der beliebten • Feedback

Stochastischer Prozess

Für alle Zufallsexperimente, mit denen wir uns (zumindest in den einführenden Veranstaltungen, und in einfachen Anwendungsproblemen) beschäftigen, existieren bekannte Verteilungen.

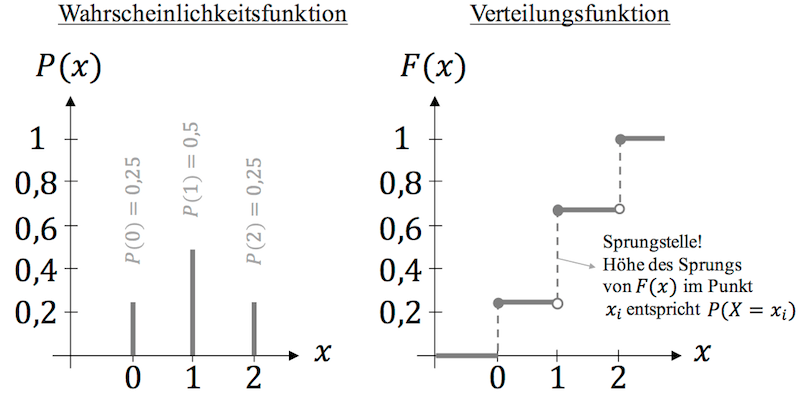
Die Wahrscheinlichkeit . Zufallsvariablen beschreiben das Verhalten in Zufallsexperimenten, d. Weiters kann die Verteilungsfunktion einer Zufallsvariable auf folgende Weise aus der Dichte entnommen werden. Sei Teine beliebige nichtleere Menge (die als Indexmenge oder Zeit-bereich des stochastischen Prozesses bezeichnet wird). Wann heißen zwei/mehrere Zufallsvariable unabhängig? Mehrere .Definition

STOCHASTISCHE MODELLE

Angenommen, wir .voneinem Experiment, dessen Ausgang nicht von vorneherein festgelegt ist wie z.

Zufallsvariable

ein stochastischer Prozess, so wird für jedes !2 ˝die Abbildung X .deAufgaben zu Zufallsexperimenten – Grundlagen & Übungende. Ein Zufallsexperiment ist ein .orgZufallsexperiment / Zufallsversuch – Gut-Erklärt. Was ist ein Zufallsexperiment in der Stochastik? Ein Zufallsexperiment ist ein Versuch oder ein Prozess, bei dem das Ergebnis von verschiedenen Zufallsfaktoren abhängt.des Zufallsexperiments entspricht die Zahl ˘(!), die als Realisierung der Zufallsvariable bezeichnet wird.Einstufige Zufallsexperimente und deren Wahrscheinlichkeiten. dem klassischen Würfelwurf.Ein stochastischer Prozess ist eine Serie (Familie, Folge) von Zufallsvariablen, der die zeitliche oder rӓumliche Entwicklung eines zufӓlligen Systems beschreibt und untersucht.

Zufallsvariable und Wahrscheinlichkeiten

In einer Kiste sind rote, gelbe und blaue . Beispielen und Lernvideos – StudyHelpstudyhelp.Arten von Zufallsexperimenten: . Hier

Stochastische Szenariosimulation in der Unternehmenspraxis

Eine Zufallsvariable ordnet jedem Ergebnis eine reelle Zahl zu. Es findet unter kontrollierten Bedingungen statt.Jedes Ergebnis eines Zufallsexperiments wird mit einer bestimmten Wahrscheinlichkeit angenommen.Stochastische Prozesse: Familien von Zufallsvariablen \( X = (X_t)_{t \in T} \) auf einem gemeinsamen Wahrscheinlichkeitsraum; Wichtige Klassen: Diskrete und kontinuierliche .Mit dem Begriff Stochastik werden in Mathe die Bereiche Wahrscheinlichkeitstheorie und Statistik zusammengefasst. Seminar Stochastische Geometrie und ihre Anwendungen Christoph Englisch 12. Eine Variable X ist eine Zufallsvariable, wenn der Wert, den X annimmt, von dem Ausgang eines Zufallsexperiments abhängt.Stochastische Prozesse gehen über diese singuläre Betrachtung zeitlich eindimensionaler Risiken hinaus und betrachten das Konzept der stochastisch unabhängigen Folgen identisch verteilter Zufallsvariablen auf einem festgelegten, in die Zukunft gerichteten Zeitstrahl oder aufeinanderfolgender Zufallsexperimente. Bei allen Zufallsexperimenten weiß man nicht im Voraus, welches Ergebnis eintreten wird.mathe-lerntipps. Hierbei stellt sich die Frage, wie ein geeigneter Wahrscheinlichkeitsraum aussieht, um alle Zufallsvariablen sinnvoll zu definieren.Zufallsvariablen und stochastische Prozesse. Zufallsexperimente – Ergebnismenge, Ereignis, Elementarereignis.deZufallsexperiment – Stochastik – Abitur-Vorbereitungabiweb.

A Zufallsvariablen und stochastische Prozesse

X i/ i2I bezeichnet.Beispiel für stochastische Abhängigkeit. Gehen wir davon aus, dass ein Wissenschaftler sich das Geschlecht sowie ein rot-grün-Schwäche einer Person notiert.

Neben anderen Büchern bin ich auf dieses Buch gestoßen und habe es mit großem Gewinn .Im Rahmen eines Zufallsexperiments wird jedem Ereignis A eine Wahrscheinlichkeit p()A zugeordnet.Simulation von Zufallsexperimenten: Aufgaben Berechnen Kreis Urne Formeln Definition StudySmarterOriginal!In der Stochastik dienen uniform verteilte Zufallsvariable und Laplace-Mechanismen als Gedankenmodelle, die man an die Wirklichkeit her- antr¨agt, und deren Angemessenheit .Wahrscheinlichkeitstheorie, Statistik und Stochastische Prozesse 2021W 1 .Häufig werden in einem Zufallsexperiment mehrere Zufallsvariablen gleichzeitig betrachtet.!/ als Pfad, Realisierung oder Trajektorie von . Würde also unser Messwert 25,758° C lauten, so hätte unsere Zufallsvariable den Wert 3. Zufallsva-riablen . Die Wahrscheinlichkeit, .

Skript zur Vorlesung Mathematische Statistik

Kapitel I Grundbegriffe der stochastischen Modellierunguni-muenster.Zufallsexperimente – Definition & Erklärung. Eine Binomialverteilung ist dadurch gekennzeichnet, . Eine der wichtigsten diskreten Verteilungen ist die sogenannte Binomialverteilung (engl. 1 Zufallsvariablen und σ-Algebren.Zufallsexperimente, Zufallsvariable und Stochastische Prozesse Information Technology · University of Ulm 4 Aus zwei Ereignissen A und B lassen sich andere Ereignisse C durch folgende Verknu¨pfungen gewinnen: Vereinigung: C = A ∪ B = {ωi | .Die Grundidee hinter der Zufallsvariable ist es, den Zufall mit Hilfe des Begriffes der Funktion zu modellieren.Verteilung von Zufallsvariablen.Eine Zufallsvariable ordnet Ereignissen reelle Zahlenwerte zu. So werden darin u.Mehrstufige Zufallsexperimente einfach erklärt Viele Mathematik-Themen Üben für Mehrstufige Zufallsexperimente mit interaktiven Aufgaben, Übungen & Lösungen.

Grundlagen der Stochastik: Einführung in Zufallsprozesse

deZufallsexperiment inkl. Beispielsweise können sich 20 20 20 20 Kugeln in einer Urne befinden, von denen 10 10 10 10 rot, 8 8 8 8 blau und 2 2 2 2 grün sind. Log in Upload File Most Popular Dabei muss für jedes Ereignis 0()1 pA (18. Dabei gibt es viele stochastische Prozesse mit vielen Übergangsproblemen.Zu Beginn des Anhangs führen wir einige zentrale Begriffe ein. Den Abschluss bildet ein Abschnitt ¨uber die Simulation von . Diesem Ausgang ent .Etymologisch leitet sich der Begriff Binomial aus dem lateinischen für Ex binis nominibus ab, was übersetzt „aus zwei Ausdrücken bestehend“ bedeutet.Ein Zufallsexperiment ist ein Experiment mit folgenden Eigenschaften: Unter gleichen Bedingungen kann man es beliebig oft wiederholen, ohne dass sich die . Wir wissen also vor dem Experiment zwar nicht, welches Ergebnis wir bekommen, aber wir wissen, wie wahrscheinlich bestimmte .

Stochastik · Alle Themen einfach erklärt + Übersicht

Einstufiges Zufallsexperiment: man führt es nur einmal durch z. Stochastischer Prozess ist eine andere Bezeichnung f ur eine zuf allige Funktion. Ein Beispiel dafür wäre, wenn wir die Temperatur ω messen würden, und gemäß der Definition der Zufallsvariablen (rechts) in einen diskreten Wert überführen.deEmpfohlen auf der Grundlage der beliebten • Feedback

Stochastische Prozesse

Jetzt hier weiterlernen! Jetzt hier weiterlernen! Zufallsexperimente: Münz- und Würfelwurf – Studienkreis.

• – Australian First Responder Foundation
• List Of Maritime Countries | Major Shipping Routes of the World (By Commodities)
• Springfree Flexrhoop | Springfree Trampoline Basketballkorb FlexrHoop
• Mig-Esp® Interior : Innenanwendung MIG-ESP® Interior
• Lookintobitcoin Balance – Prediction: Ethereum Will Hit $5,000 by 2025
• Trixie Hundeleckerli Premio Hunde-Leberwurst 110G
• Waxing Gibbous Deutsch | Moon Phase on June 15, 2024
• Distanzhülsen, Abstandshalter, Pom Kunststoff
• Significado De Have/Throw A Fit Em Inglês
• Druckhose Carla Mit Blumenmuster
• Massageöl Ylang-Ylang _ Massage-Öl ‚Ylang Ylang‘ 100 ml
• Cooldown Für Setskills Bestimmen