Zufallsvariable In R – Beispiele in R

Di: Jacob

P(erhalte einen Wert zwischen x 1 . Außerdem erklären wir, wie man die Wahrscheinlichkeit oder den . Beim Messen von physikalischen Größen (wie Länge, Masse, Volumen, Temperatur, Zeit etc. Zerlegen der Korrelationsmatrix . Wir fassen jetzt die verschiedenen Wahrscheinlichkeiten der Zufallsvariablen X in einer Wahrscheinlichkeitstabelle . replace: Ob mit Zurücklegen probiert werden soll oder nicht. Die Summe der Wahrscheinlichkeiten aller Ausprägungen beträgt .Das Konzept der Wahrscheinlichkeitsfunktion und ihr Zusammenspiel mit einer (diskreten) Zufallsvariablen ist ebenfalls in Abb. Die Binomial-Verteilung ist mit den oben beschriebenen Funktionen in R implementiert. Begriffe Stichprobenverteilung und Standardfehler erklären. DieDichte f (x ) einer stetigen . Die Wahrscheinlichkeit, dass wir in einem Intervall von a bis b einen Wert zwischen x 1 und x 2 erhalten, kann mit folgender Formel ermittelt werden:.

Wahrscheinlichkeitsverteilungen mit R

Der Zusammenhang zwischen einer beliebigen Normalverteilung N(μ, σ) und der Standard-Normalverteilung N(0, 1) wird durch die sogenannte Standardisierung einer Zufallsvariable hergestellt .1 am Beispiel der Skatkarten dargestellt: Das Zufallsexperiment besteht aus dem zufälligen Ziehen einer Karte aus dem Kartendeck und die Menge $\Omega $ umfasst alle seine 32 möglichen Ausgänge.Beispiel: Berechnen Sie die Stichproben- und Populationsvarianz in R.Eine Funktion $X$, die jedem Ergebnis $\omega$ des Ergebnisraum $\Omega$ genau eine Zahl $x$ der Menge der reellen Zahlen $\mathbb{R}$ zuordnet, heißt Zufallsvariable.1 Eindimensionale Zufallsvariablen.Schnellübersicht.Wenn eine Zufallsvariable X einer Exponentialverteilung folgt, dann kann .Wir können die Stichprobenvarianz mithilfe der Funktion var () in R berechnen: #Stichprobenvarianz berechnen var(data) [1] 46. Zufallsvariable = Funktion, bildet Elementarereignisse eines Zufallsexperiments auf Werte ab.Die Wahrscheinlichkeitsfunktion, welche es nur für diskrete Zufallsvariablen gibt, beschreibt eine diskrete Wahrscheinlichkeitsverteilung, indem sie jedem $x \in {\Bbb R}$ einer Zufallsvariablen X genau eine Wahrscheinlichkeit P aus dem Intervall $\left[ {0;1} \right]$ zuordnet. Open main menu. das der Normalverteilung folgt mit Mittelwert = 10 und sd = 3 data <-rnorm (200, mean = 10, sd = . Berechnung in R [Bearbeiten] Da das Integral über nicht geschlossen lösbar ist, benutzt man geeignete Software zur Berechnung von (). Beispielsweise lässt es sich mit den Elementarereignissen eines Münzwurfs (Wappen, Zahl) nicht allzu gut rechnen, daher werden diese über eine Zufallsvariable zu 0 und 1 . die Funktion X : Ω → R (bei reellwertigen Zufallsvariablen) Frage: Mit welcher Wahrscheinlichkeit nimmt die Zufallsvariable X einen Wert in einem Bereich A der reellen Zahlen an? Kapitel III - Zufallsvariable 2.

Stetige Zufallsvariablen

Tritt ein bestimmtes Ereignis ein, so sprichst Du von der Realisation x der Zufallsvariablen X. Jeder Eintrag von $v$ entspricht genau einem .

Statistik: Zufallsvariable, Erwartungswert, Varianz - FernUni Hagen ...

Es gibt diskrete (discrete) und stetige (continuous) Zufallsvariablen. sample(x, size, replace = FALSE, prob = NULL) wo: x: Ein Vektor von Elementen, aus denen Sie auswählen können.

Wahrscheinlichkeitsrechung für Normalverteilung in R

Zufallsvariablen mit Dichte , nennt man standardnormalverteilt. In R erhält man () durch pnorm(). Die normale Standardverteilung (auch bekannt unter Gausssche Normalverteilung) kann mit der Funktion rnorm erzeugt werden. Eine Zufallsvariable ist eine Abbildung, die jedem Element des Grundraums eine reelle Zahl zuordnet. Angenommen, wir haben den folgenden Datensatz in R: #Datensatz definieren data <-c (2, 4, 4, 7, 8, 12, 14, 15, 19, 22) Wir können die Stichprobenvarianz mithilfe der Funktion var() in R berechnen: #Stichprobenvarianz berechnen var (data) [1] 46. Bei stetigen Zufallsvariablen ist der Wert .punif (x, min, max) – berechnet die kumulative Verteilungsfunktion (cdf) für die Gleichverteilung, wobei x der Wert einer Zufallsvariablen ist und min und max die . die Wahrscheinlichkeitsdichte an der Stelle x=2 für eine standardnormalverteilte Zufallsvariable berechnen, lautet der Befehl dnorm(x=2).Das Quantil einer Zufallsvariablen ist sehr ähnlich zum empirischen Quantil von bereits gemessenen Daten definiert. Aktienrenditen, Zeitreihen, MCMC-Algorithmen und viele weitere Verfahren verwenden können durch das Erstellen korrelierter Zufallszahlen verwendet werden.1 Korrelationskoeffizient r xy nach Bravais-Pearson.Als Zufallsvektor bezeichnet man in der Stochastik eine Funktion, die auf einem Wahrscheinlichkeitsraum definiert ist, Werte im annimmt und messbar ist.Unterabschnitt diskrete Zufallsvariablen umschalten. Zufallsvektoren bilden das höherdimensionale Pendant von reellwertigen Zufallsvariablen. Ihre Verteilung lässt sich durch eine Dichtefunktion f (x) .Wie Sie in der Statistiksoftware R mit der Normal- und der Exponentialverteilung rechnen können, demonstriert Jan Mathias Köhler in diesem Video.

Zufallsvariablen, diskrete Wahrscheinlichkeitsfunktionen, stetige ...

So generieren Sie eine Normalverteilung in R (mit Beispielen)

Eine Zufallsvariable heiÿt stetig, wenn sie unendlich viele Werte x 1;:::;x k;:::annehmen kann, wie beispielsweise metrische Variablen. Die Verteilungsfunktion der stetigen Zufallsvariable kannst du hingegen analog zur Verteilungsfunktion der diskreten Zufallsvariable interpretieren. Unterabschnitt diskrete Verteilungsmodelle umschalten . Informationsgehalt#. Die Funktion rnorm wird daher verwendet, um künstliche Zufallszahlen zu simulieren. ohne Sprünge).R-Funktionen für Wahrscheinlichkeitsverteilungen

Eine Einführung in R: Dichten und Verteilungsfunktionen

Das r in rnorm steht für random numbers, also Zufallszahlen.

Beispiele in R

In diesem Kapitel lernen wir Zufallsvariablen als natürliche Darstellungsmittel für Ereignisse kennen. Schreibweise gewöhnlich: X (ω) = x (der dem .

Wahrscheinlichkeitsverteilungen in R

5 Binomial-Verteilung. Als Beispiel möchten wir z.Beispiele in R.Der einfachste Fall ist dabei eine Bernoulli-Kette, bei der die einzelnen Bernoulli-Versuche mit gleichbleibender . Hier ist wieder eingetragen, wie wahrscheinlich es ist, ein bestimmtes oder ein kleineres Ergebnis zu erhalten. Die Funktion f(x) heißt (Wahrscheinlichkeits-) Dichte von X. So ist etwa das 5%-Quantil einer Zufallsvariable genau der Wert von $X$, der den Wertebereich so aufteilt, dass $X$ zu 5% kleiner/gleich diesem Wert ist, und zu 95% größer/gleich. „ $X$ “, symbolisiert. Bezogen auf die Körpergröße .Um eine Zufallsstichprobe in R auszuwählen, können wir die Funktion sample() verwenden, die die folgende Syntax verwendet:. Zufallsvariablen mit einer stetigen Verteilungsfunktion nennt man stetige Zufallsvariablen. Somit ist für jede stetige Zufallsvariable die Wahrscheinlichkeit $P(a \le X \le b)$ gleich der Fläche zwischen dem Intervall [a, b] und der darüberliegenden Funktion f(x). Ob ein Vektor $v \in \mathbb{R}^n$ für uns Informationen enthält, hängt davon ab, wie viel wir über $v$ bereits wissen. Wie in der deskriptiven Statistik muss man beachten, dass bestimmte Begriffe nicht für alle Skalenarten sinnvoll definiert oder interpretierbar sind.Dieser Artikel befasst sich mit Zufallsvariablen und behandelt Zufallsgrößen im diskreten und stetigen Fall. wissen, dass $v$ ein Sample einer auf $\{0,1\}$ gleichverteilten Zufallsvariablen ist, wird uns nicht überraschen, wenn $v$ auch so aussieht.Eine Zufallsvariable ist eine Variable, deren numerischen Werte Ergebnisse von Zufallsexperimenten sind. Jede Ausprägung tritt meiner einer Wahrscheinlichkeit zwischen 0 und 1 auf.Die Berechnung dieser Fläche lässt sich allerdings nicht immer in so einfacher Weise geometrisch durchführen .

Verteilungen in R

Eine stetige Zufallsvariable kann in jedem beschränkten Intervall unendlich viele Ausprägungen annehmen. Diese heissen entsprechend dbinom(), pbinom(), qbinom() und rbinom() und funktionieren genau wie ihre Pendants der Standardnormalverteilung. Es gibt jedoch noch eine Vielzahl weiterer Funktionen in R, die mit dem help Befehl aufgerufen werden können?Distributions. Und wir können die .

Wahrscheinlichkeitsverteilung · Anschauliche Erklärung

size: Stichprobengröße. Werte der Zufallsvariablen werden entweder mit „ $X_{i}$ “ oder mit „ $x$ “ bezeichnet.Wenn eine Zufallsvariable X einer Exponentialverteilung folgt, dann kann die Wahrscheinlichkeitsdichtefunktion von X geschrieben werden als: f(x; λ) = λe-λx. Im folgenden wird genauer definiert, wann Zufallsvariablen diskret oder stetig sind und was für Eigenschaften diskrete und stetige Zufallsvariablen haben.

Zufallsvariable und Wahrscheinlichkeitsverteilung online lernen

Und wir können . Unabhängig von der Messgenauigkeit kann eine stetige . Der folgende Code zeigt, wie eine Normalverteilung in R generiert wird: #Machen Sie dieses Beispiel reproduzierbar set.Diskrete Zufallsvariable verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Diskrete Zufallsvariable nehmen in einem beschränkten Intervall nur endlich viele Ausprägungen an. Eine bestimmte Ausprägung kennzeichnen wir mit einem Kleinbuchstaben. Beispiel: Lackiererei Anzahl der Lackierfehler Absolute H¨auﬁgkeit 0 257 1 64 2 16 3 8 4 5 P 350 Kapitel III – Zufallsvariable 3.Das Erzeugen von korrelierten Zufallsvariablen ist einer der Kernpunkte bei der Programmierung von Simulationen.

Lernkarten diskrete Zufallsvariablen - StatsTutor

Um eine Zufallsstichprobe in R auszuwählen, können wir die Funktion sample () verwenden, die die folgende Syntax verwendet: sample (x, size, replace = .) spielen viele kleine Störeinflüsse eine Rolle, die das Messergebnis mal etwas zu hoch, mal etwas zu niedrig ausfallen lassen. Zufallsvariablen bilden ein Modell f¨ur die beobachteten Gr ¨ossen, die Daten. Wenn eine Zufallsvariable X einer Exponentialverteilung folgt, dann kann . Zufall bei wiederholter Stichprobenerhebung erkennen.Stetige Zufallsvariablen entstehen meist durch einen Messvorgang.

Korrelierte Zufallszahlen in R

Als Parameter .seed (1) # Probe von 200 Beobachtungen generieren. Wir werden später sehen: der Begriff Zufallsvariable wird genau dann genutzt, wenn wir an Erwartungswerten oder höheren Momenten interessiert sind.Stetige Zufallsvariable: Verteilungsfunktion. Stichproben und Variabilität. Diskrete Zufallsvariablen2 Mehrdimensionale Zufallsvariablen. Dann ist auch jede solche Abbildung eine Zufallsvariable.Als Zufallsvektor bezeichnet man in der Stochastik eine Funktion, die auf einem Wahrscheinlichkeitsraum definiert ist, Werte im R n {\displaystyle \mathbb {R} ^{n}} .In den vorhergehenden Abschnitten wurde des Öfteren folgende Situation betrachtet: Ein Zufallsvorgang, dessen Ergebnisse die Realisierungen einer diskreten oder stetigen Zufallsvariable X sind, wird n-mal unabhängig wiederholt. In diesem Video möchte ich erklären, wie man mit R die Wahrscheinlichkeitsfunktion oder auch die Verteilungsfunktion ausrechnen kann, am . Einführung in Zufallsvariablen Eine Zufallsvariable ist eine Funktion. 2 diskrete Verteilungsmodelle.

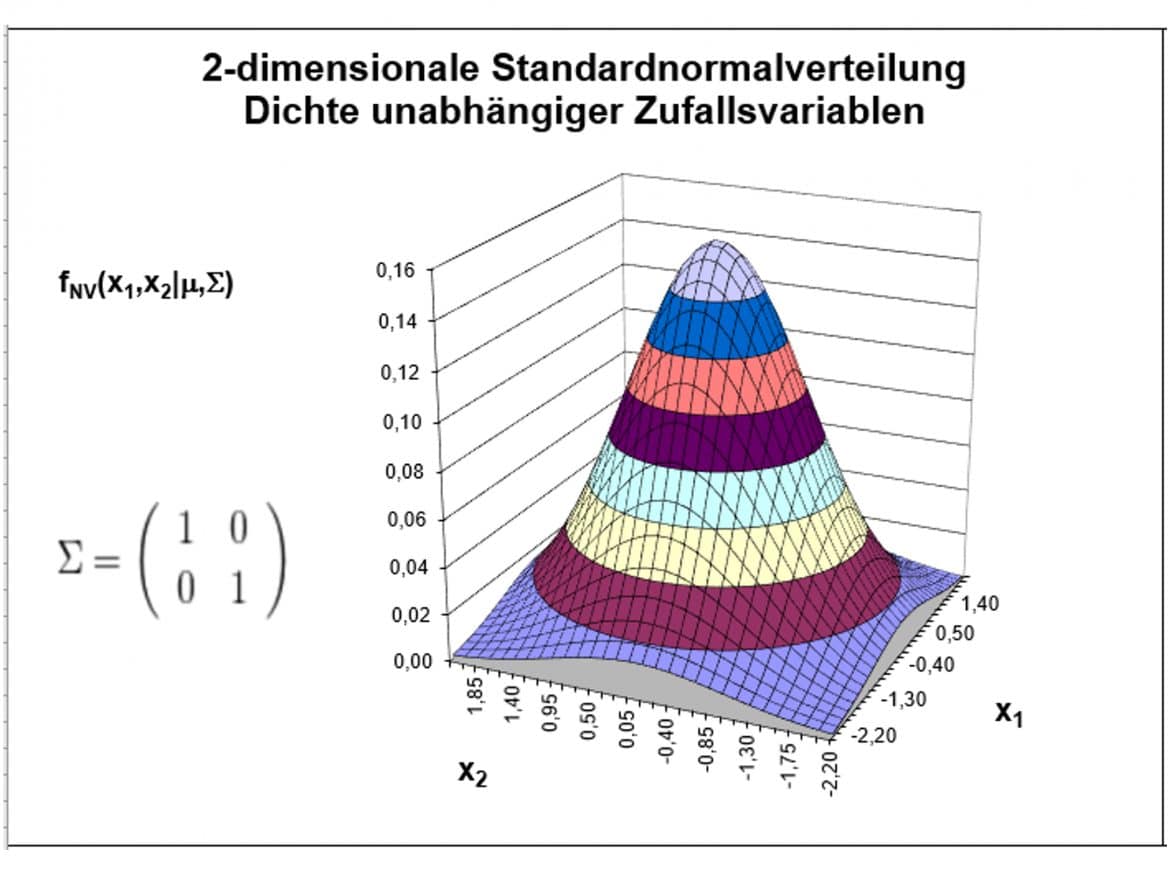
Mehrdimensionale Normalverteilung - Statistik Wiki Ratgeber Lexikon

Die erzeugten Zufallsvariablen können dabei normalverteilt oder nicht-normalverteilt sein.In der Stochastik ist eine Zufallsvariable (auch zufällige Variable, zufällige Größe, zufällige Veränderliche, zufälliges Element, Zufallselement, Zufallsveränderliche) eine Größe, .Zur Erinnerung: Wenn $\Omega$ und $\mathcal{X}$ endliche Mengen sind, dann nennen wir jede Teilmenge Ereignis. Er hält dazu ein praktisches . Üblicherweise schreibst Du die Zufallsvariable in Großbuchstaben, ihre Realisation .Beispiel: Generieren Sie eine Normalverteilung in R.

Zufallsvariablen

Korrelierte Zufallszahlen können .

18 Verteilungsfunktionen

Für weitere Plot-Beispiele zur Poisson-Verteilung siehe Abschnitt 37.Eine Gleichverteilung ist eine Wahrscheinlichkeitsverteilung, bei der jeder Wert zwischen einem Intervall von a bis b gleich wahrscheinlich gewählt wird.Viele der Eigenschaften von reellwertigen Zufallsvariablen übertragen sich direkt oder nach . Die einzelnen Ausprägungen bzw.Die andere Klasse sind stetige Verteilungsfunktionen (d. Zufallsvariablen werden mit einem lateinischen Großbuchstaben, z. Die Exponentialverteilung ist eine Wahrscheinlichkeitsverteilung, die zur Modellierung der Zeit verwendet wird, die wir warten müssen, bis ein bestimmtes Ereignis eintritt. Sie weist den möglichen Elementarereignissen eines Zufallsexperiments bestimmte Werte zu. Es gibt jedoch noch eine Vielzahl weiterer Funktionen in R, die mit dem help Befehl . Mit der Unabhängigkeit für Mengensysteme wird die stochastische Unabhängigkeit von Zufallsvariablen auch wie folgt definiert: Eine Familie von Zufallsvariablen ist genau .2 Rangkorrelationskoeffizient nach Spearman.Stetige Zufallsvariablen sind meist metrisch, zumindest aber ordinalskaliert, während diskrete Zufallsvariablen nominal-, ordinal- oder kardinalskaliert vorliegen können.

Eine Einführung in R: Dichten und Verteilungsfunktionen

Wahrscheinlichkeitstheorie Kapitel III

Eine Zufallsvariable (random variable) ist eine quantitative Variable, deren Wert durch das zuf¨alllige Ergebnis von Experimenten oder Beobachtungen bestimmt wird. 80 Zufallszahlen aus einer Normalverteilung . Besondere Bedeutung besitzen Indikatorvariablen, die nur die Werte 0 und 1 annehmen und anzeigen, ob ein Ereignis .Die Familie von Zufallsvariablen : (,,) (,), für eine beliebige Indexmenge heißt stochastisch unabhängig, falls für jede endliche Teilmenge von gilt, dass ({}) = ()für alle gilt.Die Werte, die eine Zufallsvariable annehmen kann, nennt man Ausprägung. Nennen wir unsere Zufallsvariable „Reparaturkosten“ X.

Zufallsvariable - Wahrscheinlichkeitsverteilung - YouTube

NNKJW

XSB