NNKJW

XSB

Zusammenhang Funktion : Stammfunktion

Di: Jacob

Funktionsgleichung aufstellen | InstantMathe

So kannst du berechnen, in welchen Punkten eine Funktion steigt (Ableitung größer 0), fällt (Ableitung kleiner 0) oder gleich bleibt (Ableitung gleich 0).Besteht ein graphischer Zusammenhang zwischen einer Funktion und ihrer Ableitung? Tatsächlich lassen sich aus beiden Kurven viele Informationen gewinnen, unter anderem .Ableitungen in Mathe brauchst du vor allem für die Kurvendiskussion.

Zusammenhang Ableitungen

Wenn die Lernenden immer wieder selbst funktionale Zusammenhänge entdecken und beschreiben und auf verschiedene Weise darstellen, wird eine tragfähige Grundlage für .de Playlists zu allen Mathe-Themen findet ih.Kernaussage der Eulerformel ist, dass Exponentialfunktionen mit imaginären Exponenten (e^ix) als komplexe Summe von Winkelfunktionen beschrieben . Genau wie wir Zahlen addieren, subtrahieren, multiplizieren und teilen, können wir Funktionen addieren, subtrahieren, multiplizieren und teilen.Proteine: einfach erklärt Proteine Aufbau und Struktur: Primär-, Sekundär-, Tertitär-, Quartärstruktur Proteine Funktionen mit kostenlosem Video

Funktionaler Zusammenhang

Lernende können sich dem „Wesen “ von Funktionen mit zwei Fragen nähern . Dabei untersuchst du verschiedene Fragen rund um eine Funktion und findest so heraus, wie der Graph einer .Wird die Funktion der Geschwindigkeit dann wieder abgeleitet, erhalten wir die Funktion, die die Beschleunigung in Abhängigkeit zur Zeit abbildet. Funktionen darstellen, Funktionswerte ermitteln, Graphen interpretieren und Definitionsbereich bestimmen Lineare Funktionen Autor: reinholdr.Darauf aufbauend und unter durchgängiger Nutzung verschiedener Darstellungsformen von Funktionen anhand verschiedener Beispiele kann der Begriff der Funktion als produktiv erlebt werden und zu einem funktionalen Verständnis entscheidend beitragen.

Zusammenhang: Stammfunktion, Funktion und Ableitung graphisch ...

gar nicht steigt und kann dadurch Rückschlüsse ziehen, wie der Funktionsgraph aussieht. Beispiel: Die Ableitung von f(x) = x 3 – 3x ist f'(x) = 3x 2 – 3. Der -Achsenabschnitt gibt an, wo die Gerade .Hat man eine Funktion gegeben, dann kann man aus der Ableitung zum Beispiel ablesen, wann die Funktion am stärksten steigt bzw.

Zusammenhang Funktion und Ableitungen

Lerne, Graphen zu skizzieren, Funktionsterme zu bestimmen und weitere Größen von Funktionen zu berechnen! 1.

Stammfunktionen und Integrationsregeln

Graphischer Zusammenhang von Funktion und Ableitung

In diesem Video möchte ich dir das Zusammensetzen von Funktionen vorstellen.

Ableitung: Bedeutung im Sachzusammenhang

Das ist die nachgefragte Menge bei einem Preis von null.

ln Funktion • Erklärung Beispiele · [mit Video]

Weg $~\rightarrow~$ Geschwindigkeit $~\rightarrow~$ Beschleunigung (in Abhängigkeit zur Zeit) Beispiel. Gib den Term einer Funktion f f f an, die folgende Bedingungen erfüllt.Bei der Funktionszusammensetzung wird nacheinander derselbe Wert der unabhängigen Variablen (x) in zwei oder mehr Funktionen ausgewertet.Der wichtigster Teil einer Kurvendiskussion oder der Berechnung des Flächeninhaltes mit der Integration oder graphische Darstellung von all diesen Funktionen ist der . Bildet man die . Ist die Steigung negativ, fällt die Gerade. Wenn die Lernenden immer wieder selbst funktionale Zusammenhänge entdecken und .Dieses „Wesen “ der Funktionen verstehen wir als unabhängig von der jeweiligen Darstellung oder dem Funktionstyp und bezeichnen es daher als den Kern funktionaler Zusammenhänge. Der Hauptunterschied liegt in der Perspektive und Anwendung: – Eine quadratische Funktion ist ein allgemeiner Ausdruck, der zur Beschreibung einer Beziehung dient und viele mögliche Werte \( f(x) \) für jedes \( x \) liefert.

Ableitung • leichte Erklärung mit Beispiel · [mit Video]

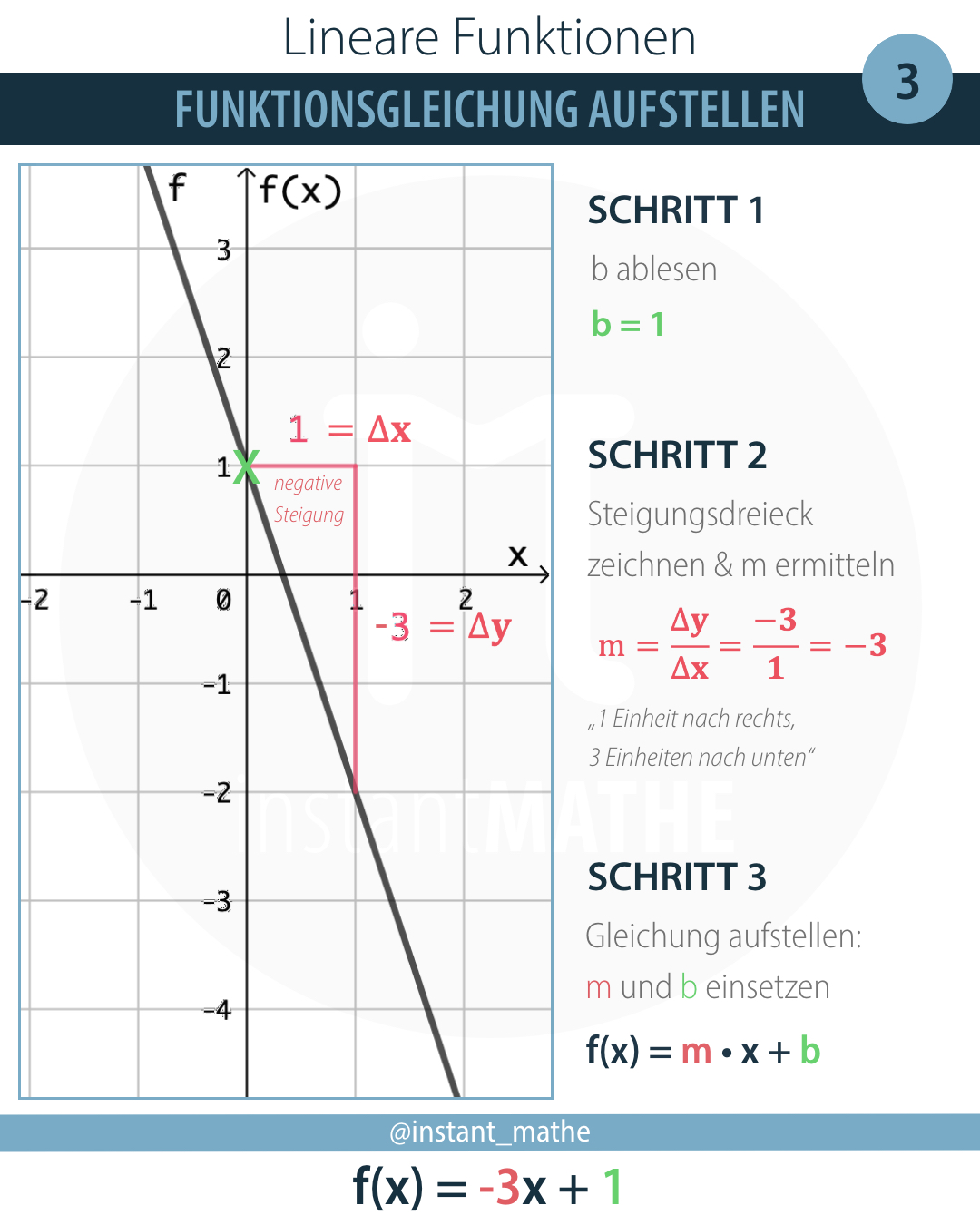
Die allgemeine Funktionsgleichung linearer Funktionen lautet: oder auch Dabei steht für die Steigung und für den -Achsenabschnitt der Funktion. Mitochondrien einfach erklärt Mitochondrien Aufbau Mitochondrien Funktion Mitochondrien Vorkommen Mitochondriale DNA Mitochondrien — häufigste FragenGeoGebra Classroom.Bei der Preis-Absatz-Funktion handelt es sich in der wirtschaftswissenschaftlichen Theorie um den Zusammenhang zwischen dem Preis eines Unternehmens und der absetzbaren Menge.

Graphischer Zusammenhang von Funktion und Ableitung - einfach erklärt

Das Zusammensetzen der . Die sogenannte Marktreaktionsformel basiert auf der Annahme, dass die abgesetzte Menge vom Preis abhängt. Du lernst leichter, wenn es dir jemand direkt erklärt und du keinen Text durcharbeiten musst? Dann . Weitere Beispiele aus dem vorangegangenen Unterricht .1 Ganzrationale Funktionen 21 1.Zusammenhang e-Funktion und natürlicher Logarithmus. Die Produktentwicklung und die Marketingabteilung .

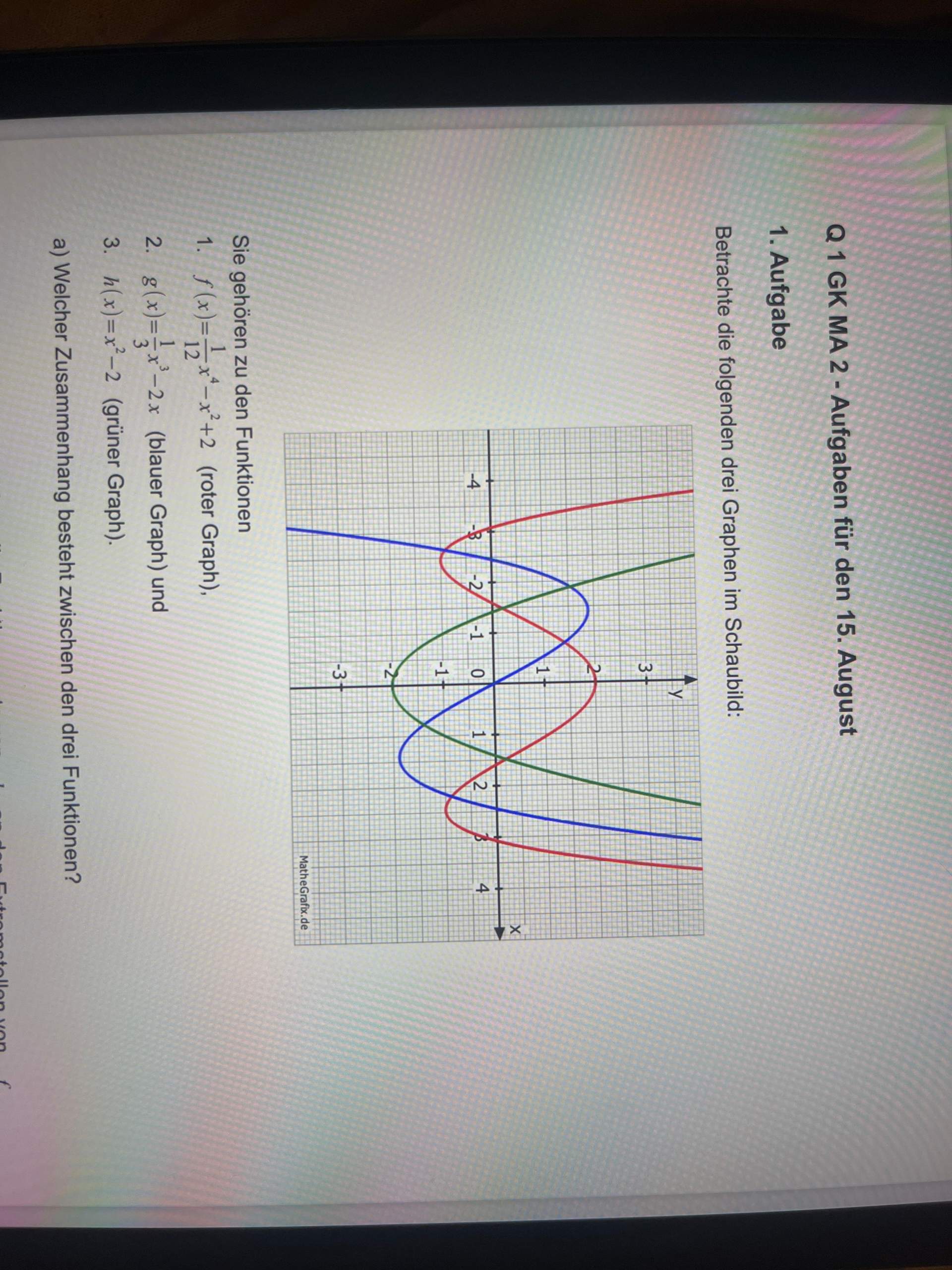
welchen zusammenhang haben diese drei funktionen? (Funktion, lineare ...

Zusammenhang und Unterschied.Die genannten Sachverhalte zeigen sich natürlich auch in einem Koordinatensystem als graphischer Zusammenhang zwischen Funktion und ihrer Ableitung.Monotoniekriterium: Zusammenhang zwischen Monotonie und Ableitung einer Funktion – Serlo „Mathe für Nicht-Freaks“ Funktionen darstellen, Funktionswerte ermitteln, Graphen interpretieren und Definitionsbereich . In den Abbildungen rechts sind der Funktionsgraph G f sowie der Graph G der Ableitungsfunktion ge-zeichnet. Je mehr Ableitungen man von einer Funktion kennt, um so genauere Aussagen kann man über den Verlauf vom Graph der .

Zusammensetzung von funktionen (zusammengesetzte funktion)

Dieser sollte entlang des Spiralcurriculums immer wieder thematisiert werden.Beim Ableiten findest du die Steigung einer Funktion in bestimmten Punkten heraus.Alle Beispiele, die wir bis jetzt gesehen habe, schaffen eine neue Funktion durch die Summe zweiter Funktionen.Was Mitochondrien sind, wie sie aufgebaut sind und welche Funktionen sie in der Zelle erfüllen, erfährst du in diesem Beitrag und in unserem Video dazu!. Inzwischen wird meine mehrfach prämierte Mathe-Lernplattform jeden Monat von bis zu 1 Million Schülern, Studenten, Eltern und Lehrern aufgerufen.Ableitung $~\rightarrow~$ 2.Eine Produktionsfunktion erklärt den Zusammenhang zwischen den Inputs und den daraus realisierbaren maximalen Output einer Unternehmung. Diese Methode dient unter anderem der Bestimmung von Extremstellen bzw.Mathematik Funktionen Ableitung von Funktionen Ableitung allgemein.In 7,5 Minuten Crashkurs wirst du viel mehr lernen als in 3 Monaten. Hier werden die Zusammenhängen zwischen einer Funktion, der Wert der 1.Wir werden uns mit der Idee vertraut machen, dass wir zwei Funktionen addieren, subtrahieren, multiplizieren oder dividieren können, um eine neue Funktion zu schaffen.Eulersche Formel einfach erklärt.

Funktionen • Mathematische Funktion einfach verstehen

Grundsätzlich lautet die gängige Annahme: Je .Beim Auffinden von Stammfunktionen bedient man sich gerne einer Tabelle in der die wichtigsten Funktionen f (x) und Ihre Ableitungsfunktionen f‘ (x) sowie die zugehörigen .Die Schülerinnen und Schüler hatten im vorangegangenen Unterricht schon mehrfach Gelegenheit Struktur-Funktions-Zusammenhänge bei Organen oder Organsystemen von Lebewesen zu entdecken. Eine lineare Funktion hat als Funktionsgraphen eine Gerade. Die Funktion geht für x → 1 x \rightarrow 1 x → 1 gegen − ∞-\infty − ∞; der Graph der Funktion ist streng . Man möchte mit der Funktion das bestmögliche Verhältnis zwischen den eingesetzten Produktionsfaktoren bestimmen, um die optimale Produktionsmenge herauszufinden. Funktion $~\rightarrow~$ 1.Nervenzelle: Neuron einfach erklärt Nervenzelle Aufbau Dendriten, Soma, Axon und synaptisches Endknöpfchen mit kostenlosem Video Die eulersche Formel, auch Eulerformel oder eulersche Gleichung genannt, fungiert als als Bindeglied zwischen trigonometrischen Funktionen und Exponentialfunktionen. Hier klicken zum . Dabei wird in die Begriffe . Der wichtigster Teil einer Kurvendiskussion oder der Berechnung des Flächeninhaltes mit . Das bedeutet, wenn man die e-Funktion und . Ableitung und . Je größer die Steigung ist, desto steiler verläuft die Gerade. Wenn man sich ins Gedächtnis ruft, worum es bei der Ableitung geht – um Steigung einer imaginären Tangente und damit um die Steigung an einem bestimmten Punkt der Kurve – dann kann man sich damit gute Eselsbrücken bauen.Die nachfolgende Illustration veranschaulicht den Zusammenhang zwischen Stammfunktion, Funktion und Ableitungsfunktion jeweils für die Differential- und die .Hier findest du gemischte Aufgaben zu Funktionen. f'(0) zum Beispiel ist .

Funktionen und ihre Graphen (Ganzrationale und gebrochenrationale ...

Im Schnittpunkt der Nachfragekurve mit der x-Achse liegt die Marktsättigung vor. Der natürliche Logarithmus ln (x) ist die inverse Funktion zur e-Funktion.Die Nachfragefunktion setzt diesen Zusammenhang von Preis und nachgefragter Menge in eine mathematische Formel. Inhaltsübersicht.Funktionaler Zusammenhang bei quadratischen Funktionen Video abspielen von YouTube Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von YouTube geladen werden. Lernen mit Serlo Zusammenhang Funktion und Ableitungen.

Stammfunktionen und Integrationsregeln

Lerne Sinus- Kosinusfunktionen ⇒ Hier lernst du die Definition, den zwei bekanntesten trigonometrische Funktionen, Sinus und Kosinus, die Definitionsmenge, Wertemenge Nullstellen, Extrema, wie sie graphisch aussehen, im direketen Vergleich mit vielen Beispielen und Graphen erklärt.Ich heiße Andreas Schneider, wurde 1989 in München geboren und lebte bis Sommer 2013 in Erding.

Zusammenhang Funktion und Ableitungen – GeoGebra

Sie ist nützlich in der Analyse von Bewegungen, wirtschaftlichen Modellen, und vielen . Was bedeutet es, Funktionen zusammenzusetzen? Es bedeutet, eine Funktion zu .Aufgrund des Hauptsatzes der Differential- und Integralrechnung besteht zwischen einer (differenzierbaren) Funktion f(x) und ihrer Ableitung f'(x) folgender Zusammenhang: ∫ .8 Zusammenhang zwischen den Graphen von Funktion und Ableitungsfunktion Die Ableitung y fx () gibt anschaulich die Steigung des Funktionsgraphen G f an der Stelle x an.Als lineare Funktion wird oft (insbesondere in der Schulmathematik) eine Funktion: der Form = +;,,also eine Polynomfunktion höchstens ersten Grades bezeichnet.Funktionen und Gleichungen lösen, Zusammenhang, AnalysisWenn noch spezielle Fragen sind: https://www. In einer Stunde wird das Phänomen an einem geeigneten konkreten Beispiel thematisiert.Der Realteil einer holomorphen Funktion ist harmonisch, wie aus den Cauchy-Riemann-Differentialgleichungen folgt, interessanterweise gilt auch die Umkehrung, d. Aber du kannst zwei Funktionen auch subtrahieren, . Es handelt sich dabei jedoch nicht um eine lineare Abbildung im Sinne der linearen Algebra, sondern um eine affine Abbildung, da die Linearitätsbedingung im Allgemeinen nicht erfüllt ist.Stammfunktion einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

Wichtige Stammfunktionen: Tabelle & Beispiele I StudySmarter

Autor: Einfach Mathe!

Stammfunktion

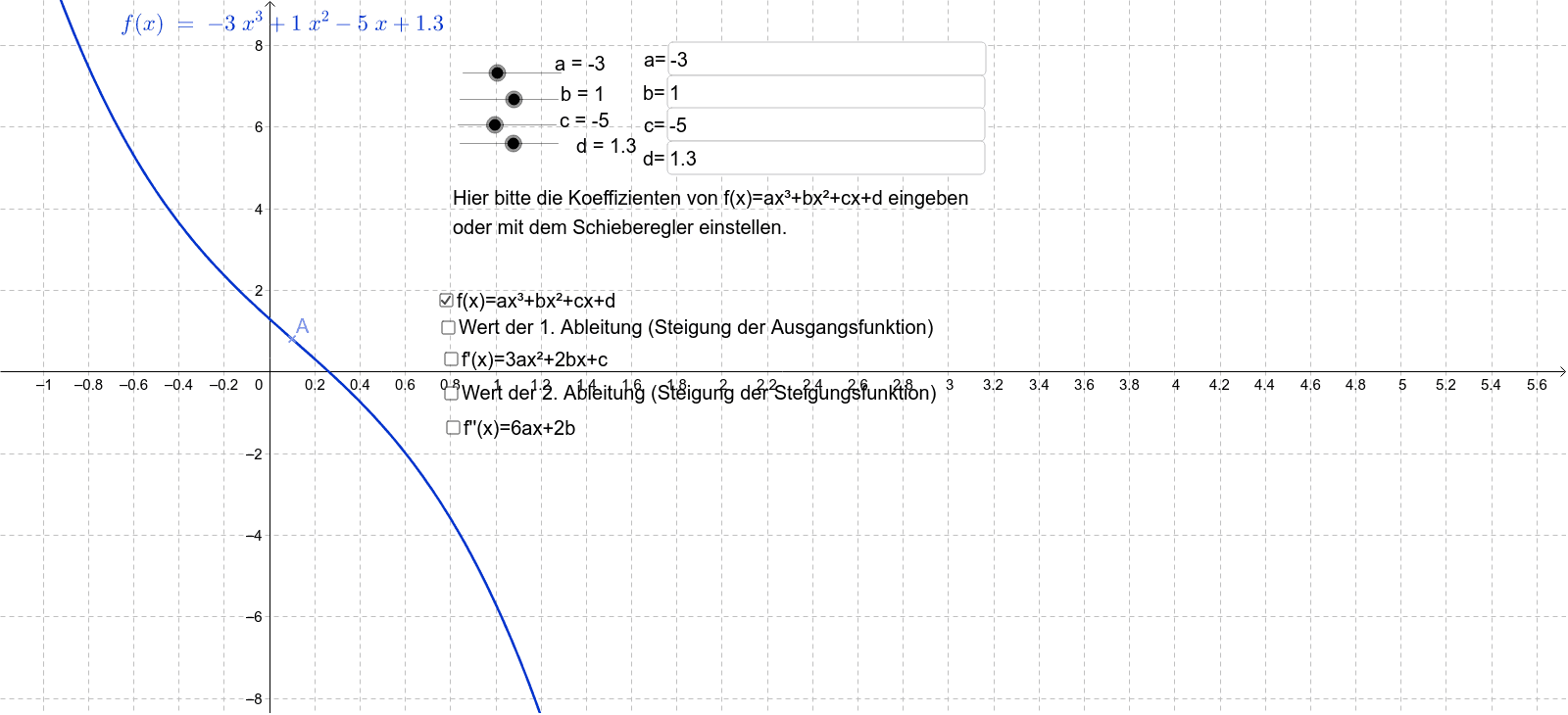
Die grafische Darstellung der Funktion wird dann als Nachfragekurve bezeichnet. Die Ableitung einer Funktion f f an einer Stelle x x gibt die Steigung des Graphen der .Wie du sie für die verschiedenen Funktionen berechnest, erklären wir dir hier anschaulich und mit vielen Beispielen.Um Funktionen zu untersuchen und ihre Eigenschaften zu verstehen, gibt es verschiedene Möglichkeiten und Grundlagen, die du kennen solltest. Die Abbildung zeigt die Ausgangsfunktion mit ihrer ersten, zweiten und dritten Ableitung:

Funktionaler Zusammenhang bei quadratischen Funktionen

Funktionsgleichung

Video ansehen7:33In diesem Video spreche ich mit dir über den graphischen Zusammenhand von der Ausgangsfunktion und der ersten und zweiten Ableitung! Ich erkläre dir, wie man.Zu Funktionale Zusammenhänge im Teil A gehören folgende Inhalte. Eine gute Veranschaulichung für den Zusammenhang zwischen primären und sekundären betrieblichen Funktionen bietet das Beispiel eines Autokonzerns.

Prinzip Struktur und Funktion

Zusammenhang Stammfunktion F(x) – Funktion f(x) – Ableitungsfunktion f'(x) Beim Auffinden von Stammfunktionen bedient man sich gerne einer Tabelle in der die wichtigsten Funktionen f(x) und Ihre Ableitungsfunktionen f'(x) sowie die zugehörigen Stammfunktionen F(x) angeführt sind.Im Bereich der Programmierung, insbesondere im Zusammenhang mit Visual Basic for Applications (VBA) von Microsoft, erweist sich die Funktion „GetTempName“ als . Kurz nach meiner Auswanderung nach Málaga (Spanien) habe ich begonnen, an der Mathebibel zu arbeiten.Was bedeutet Funktionaler Zusammenhang? Die „Leitidee Funktionaler Zusammenhang“ ist eine von fünf Leitideen, der inhaltsbezogene mathematische Kompetenzen .Zusammenhang zwischen höheren Ableitungen. Die Summe zweier .Die Ableitung bezeichnest du mit f'(x).Unter der Leitidee Funktionaler Zusammenhang versteht man bei den Mathematik-Standards die Fähigkeit, aus dem Wert von einer (oder mehrerer) Größe (n) auf den .

Graphischer Zusammenhang von f und f‘ und f“

Wenn Sie die Funktion f(x) und ihre dazugehörige Ableitung f'(x) graphisch darstellen, also beispielsweise mithilfe einer Wertetabelle in ein passendes Koordinatensystem .Zusammenhang Ableitungen. jede harmonische Funktion ist Realteil einer holomorphen Funktion.Betriebliche Funktionen: Beispiele Einfach erklärt Primäre Sekundäre Definition Grundfunktionen BWL Lerninhalte finden .